zeth.core.mimc.MiMCBase Class Reference

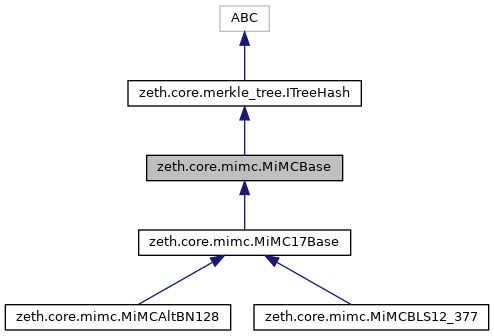
Inheritance diagram for zeth.core.mimc.MiMCBase:

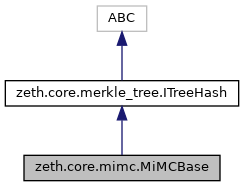
Collaboration diagram for zeth.core.mimc.MiMCBase:

Public Member Functions
def	__init__ (self, str seed_str, int prime, int num_rounds)
int	encrypt (self, int message, int ek)
bytes	hash (self, bytes left, bytes right)
int	hash_int (self, int x, int y)
int	mimc_round (self, int message, int key, int rc)

Public Attributes
	seed
	prime
	num_rounds

Detailed Description

Base class of MiMC implementations.

Definition at line 28 of file mimc.py.

Constructor & Destructor Documentation

__init__()

def zeth.core.mimc.MiMCBase.__init__	(		self,
		str	seed_str,
		int	prime,
		int	num_rounds
	)

Definition at line 32 of file mimc.py.

    def __init__(
            self,
            seed_str: str,
            prime: int,
            num_rounds: int):
        self.seed = _keccak_256(_str_to_bytes(seed_str))
        self.prime = prime
        self.num_rounds = num_rounds
 

Member Function Documentation

encrypt()

int zeth.core.mimc.MiMCBase.encrypt	(		self,
		int	message,
		int	ek
	)

Definition at line 41 of file mimc.py.

    def encrypt(
            self,
            message: int,
            ek: int) -> int:
        result = message % self.prime
        key = ek % self.prime
        round_constant: int = self.seed
 
        # The round constant in round 0 is 0 (see [AGRRT16])
        result = self.mimc_round(result, key, 0)
 
        for _ in range(self.num_rounds - 1):
            round_constant = _update_round_constant(round_constant)
            result = self.mimc_round(result, key, round_constant)
 
        # Add key to the final result (see [AGRRT16])
        return (result + key) % self.prime
 

Here is the call graph for this function:

Here is the caller graph for this function:

hash()

bytes zeth.core.mimc.MiMCBase.hash	(		self,
		bytes	left,
		bytes	right
	)

Apply Miyaguchi-Preneel to the output of the encrypt function.

Reimplemented from zeth.core.merkle_tree.ITreeHash.

Definition at line 59 of file mimc.py.

    def hash(self, left: bytes, right: bytes) -> bytes:
        """
        Apply Miyaguchi-Preneel to the output of the encrypt function.
        """
        x = int.from_bytes(left, byteorder='big') % self.prime
        y = int.from_bytes(right, byteorder='big') % self.prime
        return self.hash_int(x, y).to_bytes(32, byteorder='big')
 

Here is the call graph for this function:

hash_int()

int zeth.core.mimc.MiMCBase.hash_int	(		self,
		int	x,
		int	y
	)

Similar to hash, but use field elements directly.

Definition at line 67 of file mimc.py.

    def hash_int(self, x: int, y: int) -> int:
        """
        Similar to hash, but use field elements directly.
        """
        assert x < self.prime
        assert y < self.prime
        return (self.encrypt(x, y) + x + y) % self.prime
 

Here is the call graph for this function:

Here is the caller graph for this function:

mimc_round()

int zeth.core.mimc.MiMCBase.mimc_round	(		self,
		int	message,
		int	key,
		int	rc
	)

Reimplemented in zeth.core.mimc.MiMC17Base.

Definition at line 76 of file mimc.py.

    def mimc_round(self, message: int, key: int, rc: int) -> int:
        pass
 
 

Here is the caller graph for this function:

Member Data Documentation

num_rounds

zeth.core.mimc.MiMCBase.num_rounds

Definition at line 35 of file mimc.py.

prime

zeth.core.mimc.MiMCBase.prime

Definition at line 34 of file mimc.py.

seed

zeth.core.mimc.MiMCBase.seed

Definition at line 33 of file mimc.py.

---

The documentation for this class was generated from the following file:

• /home/runner/work/zeth/zeth/client/zeth/core/mimc.py