zeth.core.signing Namespace Reference

Classes
class	SigningKeyPair
class	SigningSecretKey
class	SigningVerificationKey

Functions
SigningKeyPair	gen_signing_keypair ()
bytes	signature_to_bytes (Signature signature)
Signature	signature_from_bytes (bytes sig_bytes)
Signature	sign (SigningSecretKey sk, bytes m)
bool	verify (SigningVerificationKey vk, bytes m, int sigma)
List[int]	verification_key_as_mix_parameter (SigningVerificationKey vk)
SigningVerificationKey	verification_key_from_mix_parameter (List[int] param)
int	signature_as_mix_parameter (Signature signature)
Signature	signature_from_mix_parameter (int param)
bytes	fq_to_bytes (FQ fq_element)
FQ	fq_from_bytes (bytes fq_bytes)
str	fq_to_hex (FQ fq_element)
FQ	fq_from_hex (str fq_hex)
bytes	g1_to_bytes (G1 group_el)
Dict[str, Any]	g1_to_json_dict (G1 group_el)
G1	g1_from_json_dict (Dict[str, Any] json_dict)

Variables
	FQ = ec.FQ
	G1 = Tuple[ec.FQ, ec.FQ]
	Signature = int

Function Documentation

fq_from_bytes()

FQ zeth.core.signing.fq_from_bytes

(

bytes

fq_bytes

)

Definition at line 205 of file signing.py.

def fq_from_bytes(fq_bytes: bytes) -> FQ:
    return FQ(int.from_bytes(fq_bytes, byteorder='big'))
 
 

Here is the caller graph for this function:

fq_from_hex()

FQ zeth.core.signing.fq_from_hex

(

str

fq_hex

)

Definition at line 213 of file signing.py.

def fq_from_hex(fq_hex: str) -> FQ:
    return fq_from_bytes(bytes.fromhex(fq_hex))
 
 

Here is the call graph for this function:

Here is the caller graph for this function:

fq_to_bytes()

bytes zeth.core.signing.fq_to_bytes

(

FQ

fq_element

)

Definition at line 201 of file signing.py.

def fq_to_bytes(fq_element: FQ) -> bytes:
    return int(fq_element.n).to_bytes(32, byteorder='big')
 
 

Here is the caller graph for this function:

fq_to_hex()

str zeth.core.signing.fq_to_hex

(

FQ

fq_element

)

Definition at line 209 of file signing.py.

def fq_to_hex(fq_element: FQ) -> str:
    return fq_to_bytes(fq_element).hex()
 
 

Here is the call graph for this function:

Here is the caller graph for this function:

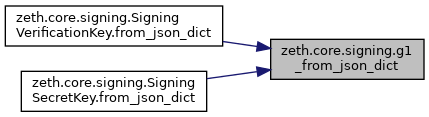
g1_from_json_dict()

G1 zeth.core.signing.g1_from_json_dict

(

Dict[str, Any]

json_dict

)

Definition at line 235 of file signing.py.

def g1_from_json_dict(json_dict: Dict[str, Any]) -> G1:
    return (fq_from_hex(json_dict["x"]), fq_from_hex(json_dict["y"]))

Here is the call graph for this function:

Here is the caller graph for this function:

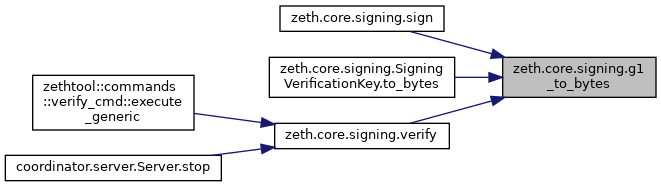
g1_to_bytes()

bytes zeth.core.signing.g1_to_bytes

(

G1

group_el

)

Encode a group element into a byte string
We assume here the group prime $p$ is written in less than 256 bits
to conform with Ethereum bytes32 type.

Definition at line 217 of file signing.py.

def g1_to_bytes(group_el: G1) -> bytes:
    """
    Encode a group element into a byte string
    We assume here the group prime $p$ is written in less than 256 bits
    to conform with Ethereum bytes32 type.
    """
    return \
        int(group_el[0]).to_bytes(32, byteorder='big') + \
        int(group_el[1]).to_bytes(32, byteorder='big')
 
 

Here is the caller graph for this function:

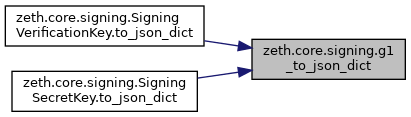
g1_to_json_dict()

Dict[str, Any] zeth.core.signing.g1_to_json_dict

(

G1

group_el

)

Definition at line 228 of file signing.py.

def g1_to_json_dict(group_el: G1) -> Dict[str, Any]:
    return {
        "x": fq_to_hex(group_el[0]),
        "y": fq_to_hex(group_el[1]),
    }
 
 

Here is the call graph for this function:

Here is the caller graph for this function:

gen_signing_keypair()

SigningKeyPair zeth.core.signing.gen_signing_keypair

(

)

Return a one-time signature key-pair
composed of elements of F_q and G1.

Definition at line 93 of file signing.py.

def gen_signing_keypair() -> SigningKeyPair:
    """
    Return a one-time signature key-pair
    composed of elements of F_q and G1.
    """
    key_size_byte = ceil(len("{0:b}".format(ec.curve_order)) / 8)
    x = FQ(
        int(bytes(urandom(key_size_byte)).hex(), 16) % ec.curve_order)
    y = FQ(
        int(bytes(urandom(key_size_byte)).hex(), 16) % ec.curve_order)
    X = ec.multiply(ec.G1, x.n)
    Y = ec.multiply(ec.G1, y.n)
 
    # We include y_g1 in the signing key
    sk = SigningSecretKey(x, y, Y)
    vk = SigningVerificationKey(X, Y)
    return SigningKeyPair(sk, vk)
 
 

sign()

Signature zeth.core.signing.sign	(	SigningSecretKey	sk,
		bytes	m
	)

Generate a Schnorr signature on a message m.
We assume here that the message fits in an Ethereum word (i.e. bit_len(m)
<= 256), so that it can be represented by a single bytes32 on the smart-
contract during the signature verification.

Definition at line 123 of file signing.py.

def sign(
        sk: SigningSecretKey,
        m: bytes) -> Signature:
    """
    Generate a Schnorr signature on a message m.
    We assume here that the message fits in an Ethereum word (i.e. bit_len(m)
    <= 256), so that it can be represented by a single bytes32 on the smart-
    contract during the signature verification.
    """
 
    # Encode and hash the verifying key and input hashes
    challenge_to_hash = g1_to_bytes(sk.ssk[1]) + m
 
    # Convert the hex digest into a field element
    challenge = int(sha256(challenge_to_hash).hexdigest(), 16)
    challenge = challenge % ec.curve_order
 
    # Compute the signature sigma
    sigma = (sk.ssk[0].n + challenge * sk.psk.n) % ec.curve_order
    return sigma
 
 

Here is the call graph for this function:

signature_as_mix_parameter()

int zeth.core.signing.signature_as_mix_parameter

(

Signature

signature

)

Transform a signature to the format required by the mix function.

Definition at line 183 of file signing.py.

def signature_as_mix_parameter(signature: Signature) -> int:
    """
    Transform a signature to the format required by the mix function.
    """
    # This function happens to be the identity but in the general case some
    # transform will be required.
    return signature
 
 

signature_from_bytes()

Signature zeth.core.signing.signature_from_bytes

(

bytes

sig_bytes

)

Definition at line 119 of file signing.py.

def signature_from_bytes(sig_bytes: bytes) -> Signature:
    return int.from_bytes(sig_bytes, byteorder='big')
 
 

signature_from_mix_parameter()

Signature zeth.core.signing.signature_from_mix_parameter

(

int

param

)

Transform mix function parameters to a signature.

Definition at line 192 of file signing.py.

def signature_from_mix_parameter(param: int) -> Signature:
    """
    Transform mix function parameters to a signature.
    """
    return param
 
# Low level encoding / decoding functions
 
 

signature_to_bytes()

bytes zeth.core.signing.signature_to_bytes

(

Signature

signature

)

Definition at line 115 of file signing.py.

def signature_to_bytes(signature: Signature) -> bytes:
    return signature.to_bytes(32, byteorder='big')
 
 

verification_key_as_mix_parameter()

List[int] zeth.core.signing.verification_key_as_mix_parameter

(

SigningVerificationKey

vk

)

Transform a verification key to the format required by the mix function.

Definition at line 166 of file signing.py.

def verification_key_as_mix_parameter(vk: SigningVerificationKey) -> List[int]:
    """
    Transform a verification key to the format required by the mix function.
    """
    return [int(vk.ppk[0]), int(vk.ppk[1]), int(vk.spk[0]), int(vk.spk[1])]
 
 

verification_key_from_mix_parameter()

SigningVerificationKey zeth.core.signing.verification_key_from_mix_parameter

(

List[int]

param

)

Transform mix function parameter to verification key.

Definition at line 173 of file signing.py.

def verification_key_from_mix_parameter(
        param: List[int]) -> SigningVerificationKey:
    """
    Transform mix function parameter to verification key.
    """
    return SigningVerificationKey(
        (FQ(param[0]), FQ(param[1])),
        (FQ(param[2]), FQ(param[3])))
 
 

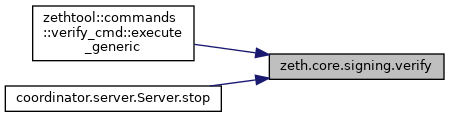
verify()

bool zeth.core.signing.verify	(	SigningVerificationKey	vk,
		bytes	m,
		int	sigma
	)

Return true if the signature sigma is valid on message m and vk.
We assume here that the message is an hexadecimal string written in
less than 256 bits to conform with Ethereum bytes32 type.

Definition at line 145 of file signing.py.

def verify(
        vk: SigningVerificationKey,
        m: bytes,
        sigma: int) -> bool:
    """
    Return true if the signature sigma is valid on message m and vk.
    We assume here that the message is an hexadecimal string written in
    less than 256 bits to conform with Ethereum bytes32 type.
    """
    # Encode and hash the verifying key and input hashes
    challenge_to_hash = g1_to_bytes(vk.spk) + m
 
    challenge = int(sha256(challenge_to_hash).hexdigest(), 16)
    challenge = challenge % ec.curve_order
 
    left_part = ec.multiply(ec.G1, FQ(sigma).n)
    right_part = ec.add(vk.spk, ec.multiply(vk.ppk, FQ(challenge).n))
 
    return ec.eq(left_part, right_part)
 
 

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

FQ

zeth.core.signing.FQ = ec.FQ

Definition at line 21 of file signing.py.

G1

zeth.core.signing.G1 = Tuple[ec.FQ, ec.FQ]

Definition at line 22 of file signing.py.

Signature

zeth.core.signing.Signature = int

Definition at line 112 of file signing.py.