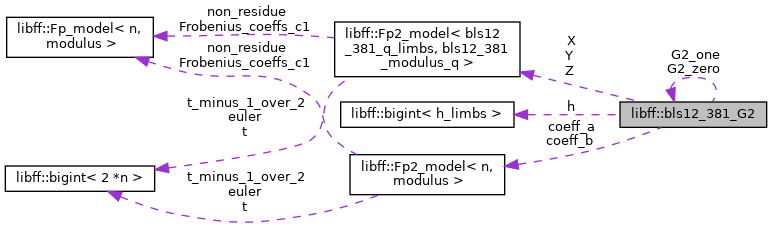
#include <bls12_381_g2.hpp>
Definition at line 21 of file bls12_381_g2.hpp.
◆ base_field
◆ scalar_field
◆ twist_field
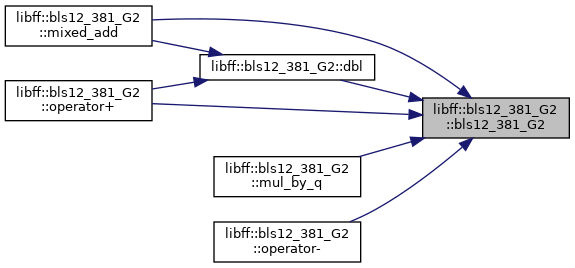
◆ bls12_381_G2() [1/2]
| libff::bls12_381_G2::bls12_381_G2 |
( |
| ) |
|
◆ bls12_381_G2() [2/2]
◆ add()
◆ base_field_char()
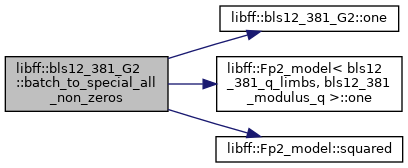
◆ batch_to_special_all_non_zeros()
| void libff::bls12_381_G2::batch_to_special_all_non_zeros |
( |
std::vector< bls12_381_G2 > & |
vec | ) |
|
|
static |
Definition at line 463 of file bls12_381_g2.cpp.
466 std::vector<bls12_381_Fq2> Z_vec;
467 Z_vec.reserve(vec.size());
469 for (
auto &el : vec) {
470 Z_vec.emplace_back(el.Z);
472 batch_invert<bls12_381_Fq2>(Z_vec);
476 for (
size_t i = 0; i < vec.size(); ++i) {
480 vec[i].X = vec[i].X * Z2;
481 vec[i].Y = vec[i].Y * Z3;
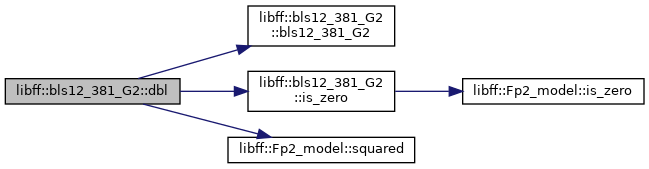
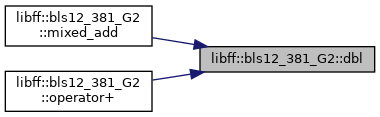
◆ dbl()
Definition at line 283 of file bls12_381_g2.cpp.
285 #ifdef PROFILE_OP_COUNTS
312 eightC = eightC + eightC;
313 eightC = eightC + eightC;
◆ is_in_safe_subgroup()
| bool libff::bls12_381_G2::is_in_safe_subgroup |
( |
| ) |
const |
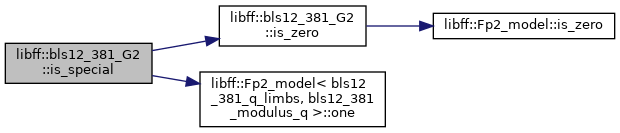
◆ is_special()
| bool libff::bls12_381_G2::is_special |
( |
| ) |
const |
◆ is_well_formed()
| bool libff::bls12_381_G2::is_well_formed |
( |
| ) |
const |
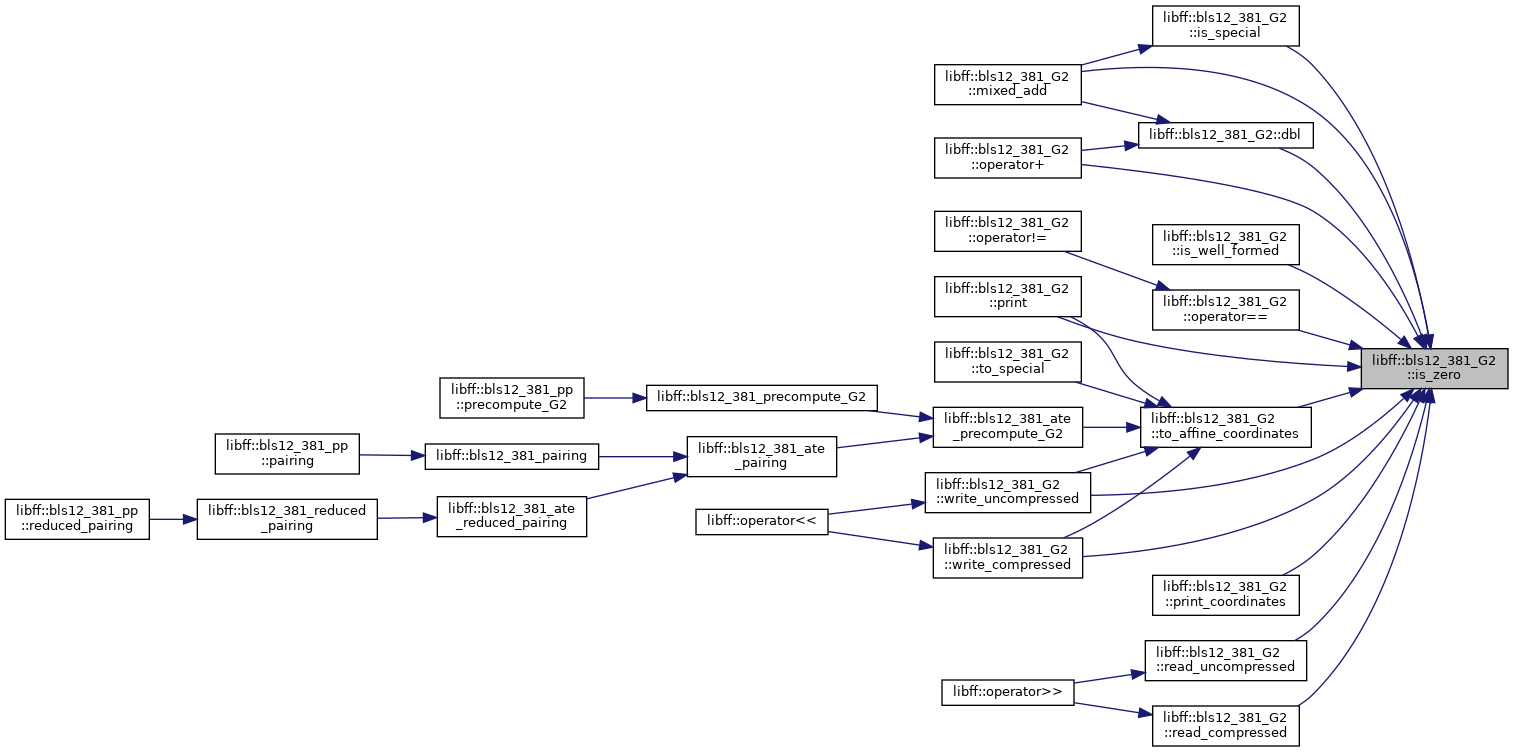
◆ is_zero()
| bool libff::bls12_381_G2::is_zero |
( |
| ) |
const |
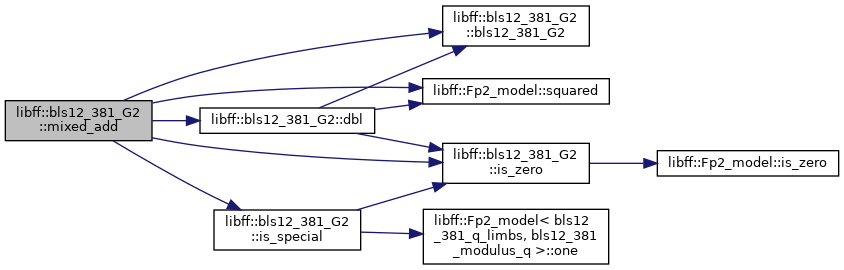
◆ mixed_add()
Definition at line 214 of file bls12_381_g2.cpp.
217 assert(other.is_special());
225 if (other.is_zero()) {
247 if (this->
X == U2 && this->
Y == S2) {
252 #ifdef PROFILE_OP_COUNTS
276 Y3 = r * (V - X3) - Y3 - Y3;
◆ mul_by_b()
◆ mul_by_cofactor()
◆ mul_by_q()
◆ one()
◆ operator!=()
| bool libff::bls12_381_G2::operator!= |
( |
const bls12_381_G2 & |
other | ) |
const |
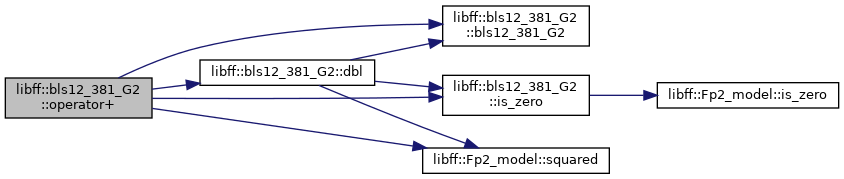
◆ operator+()
Definition at line 136 of file bls12_381_g2.cpp.
143 if (other.is_zero()) {
171 if (U1 == U2 && S1 == S2) {
194 bls12_381_Fq2 Z3 = ((this->
Z + other.Z).squared() - Z1Z1 - Z2Z2) * H;
◆ operator-() [1/2]
◆ operator-() [2/2]
◆ operator==()
| bool libff::bls12_381_G2::operator== |
( |
const bls12_381_G2 & |
other | ) |
const |
Definition at line 100 of file bls12_381_g2.cpp.
103 return other.is_zero();
106 if (other.is_zero()) {
123 if (((this->
X * Z2_squared) != (other.X * Z1_squared)) ||
124 ((this->
Y * Z2_cubed) != (other.Y * Z1_cubed))) {
◆ order()
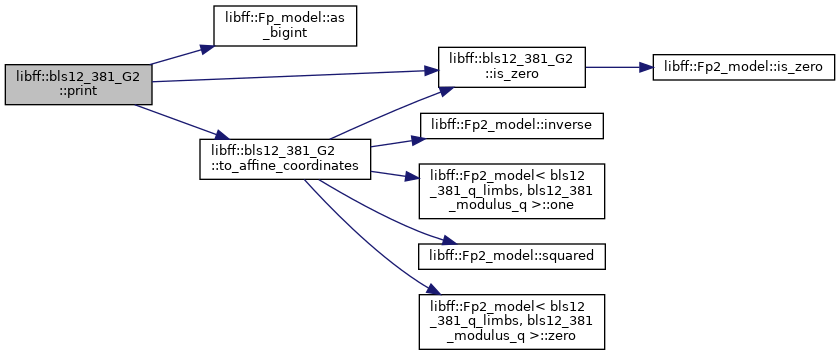
◆ print()
| void libff::bls12_381_G2::print |
( |
| ) |
const |
Definition at line 33 of file bls12_381_g2.cpp.
39 copy.to_affine_coordinates();
41 "(%Nd*z + %Nd , %Nd*z + %Nd)\n",
42 copy.X.coeffs[1].as_bigint().data,
44 copy.X.coeffs[0].as_bigint().data,
46 copy.Y.coeffs[1].as_bigint().data,
48 copy.Y.coeffs[0].as_bigint().data,
◆ print_coordinates()
| void libff::bls12_381_G2::print_coordinates |
( |
| ) |
const |
Definition at line 53 of file bls12_381_g2.cpp.
59 "(%Nd*z + %Nd : %Nd*z + %Nd : %Nd*z + %Nd)\n",
62 this->X.coeffs[0].as_bigint().data,
64 this->Y.coeffs[1].as_bigint().data,
66 this->Y.coeffs[0].as_bigint().data,
68 this->Z.coeffs[1].as_bigint().data,
70 this->Z.coeffs[0].as_bigint().data,
◆ random_element()
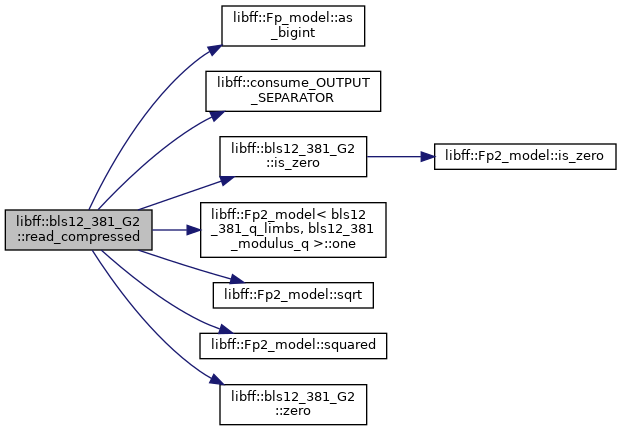
◆ read_compressed()
| void libff::bls12_381_G2::read_compressed |
( |
std::istream & |
in, |
|
|
bls12_381_G2 & |
g |
|
) |
| |
|
static |
Definition at line 410 of file bls12_381_g2.cpp.
422 in.read((
char *)&Y_lsb, 1);
431 if ((tY.coeffs[0].as_bigint().data[0] & 1) != Y_lsb) {
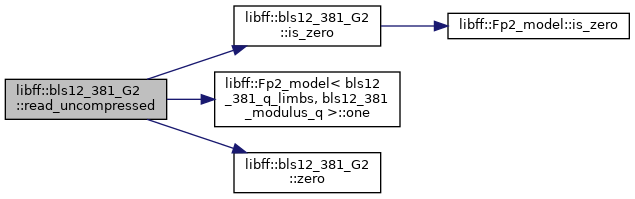
◆ read_uncompressed()
| void libff::bls12_381_G2::read_uncompressed |
( |
std::istream & |
in, |
|
|
bls12_381_G2 & |
g |
|
) |
| |
|
static |
◆ size_in_bits()
| static std::size_t libff::bls12_381_G2::size_in_bits |
( |
| ) |
|
|
inlinestatic |
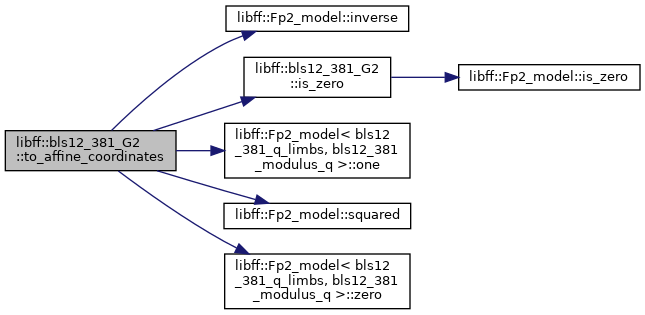
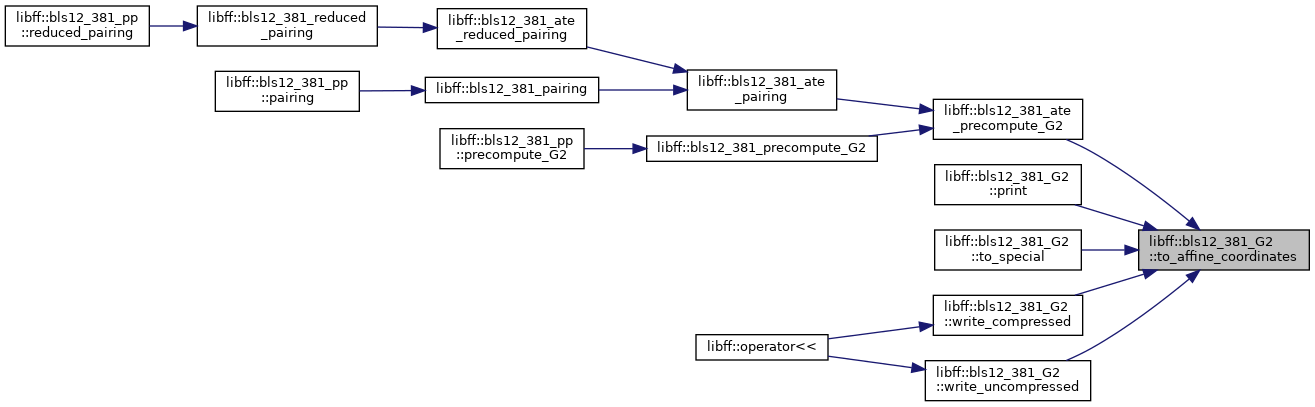
◆ to_affine_coordinates()
| void libff::bls12_381_G2::to_affine_coordinates |
( |
| ) |
|
◆ to_special()
| void libff::bls12_381_G2::to_special |
( |
| ) |
|
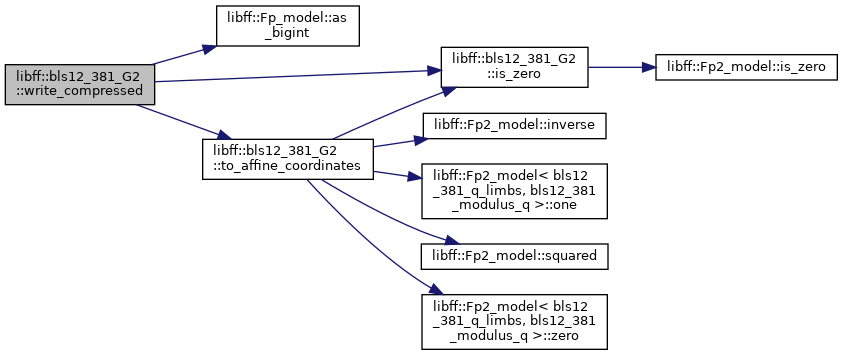
◆ write_compressed()
| void libff::bls12_381_G2::write_compressed |
( |
std::ostream & |
out | ) |
const |
Definition at line 384 of file bls12_381_g2.cpp.
387 copy.to_affine_coordinates();
391 << (copy.Y.coeffs[0].as_bigint().data[0] & 1);
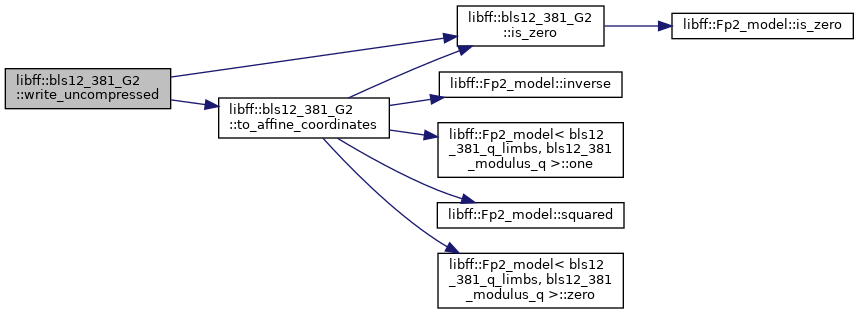
◆ write_uncompressed()
| void libff::bls12_381_G2::write_uncompressed |
( |
std::ostream & |
out | ) |
const |
◆ zero()
◆ coeff_a
◆ coeff_b
◆ fixed_base_exp_window_table
| std::vector< size_t > libff::bls12_381_G2::fixed_base_exp_window_table |
|
static |
◆ G2_one
◆ G2_zero
◆ h_bitcount
| const mp_size_t libff::bls12_381_G2::h_bitcount = 507 |
|
static |
◆ h_limbs
| const mp_size_t libff::bls12_381_G2::h_limbs |
|
static |
◆ wnaf_window_table
| std::vector< size_t > libff::bls12_381_G2::wnaf_window_table |
|
static |
The documentation for this class was generated from the following files:


















 1.8.17
1.8.17