Namespaces | |
| ffi | |
Enumerations | |
| enum | multi_exp_method { multi_exp_method_naive, multi_exp_method_naive_plain, multi_exp_method_bos_coster, multi_exp_method_BDLO12, multi_exp_method_BDLO12_signed } |
| enum | multi_exp_base_form { multi_exp_base_form_normal, multi_exp_base_form_special } |
| Form of base elements passed to multi_exp routines. More... | |
| enum | encoding_t : uint8_t { encoding_binary = 0, encoding_json = 1 } |
| Encodings for (de)serialization. More... | |
| enum | form_t : uint8_t { form_plain = 0, form_montgomery = 1 } |
| Encodings for (de)serialization. More... | |
| enum | compression_t : uint8_t { compression_off = 0, compression_on = 1 } |
| Enable / disable compression in (de)serialization. More... | |
Functions | |
| std::ostream & | operator<< (std::ostream &out, const alt_bn128_G1 &g) |
| std::istream & | operator>> (std::istream &in, alt_bn128_G1 &g) |
| template<mp_size_t m> | |
| alt_bn128_G1 | operator* (const bigint< m > &lhs, const alt_bn128_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| alt_bn128_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const alt_bn128_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const alt_bn128_G2 &g) |
| std::istream & | operator>> (std::istream &in, alt_bn128_G2 &g) |
| template<mp_size_t m> | |
| alt_bn128_G2 | operator* (const bigint< m > &lhs, const alt_bn128_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| alt_bn128_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const alt_bn128_G2 &rhs) |
| void | init_alt_bn128_params () |
| std::ostream & | operator<< (std::ostream &out, const alt_bn128_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, alt_bn128_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const alt_bn128_ate_ell_coeffs &c) |
| std::istream & | operator>> (std::istream &in, alt_bn128_ate_ell_coeffs &c) |
| std::ostream & | operator<< (std::ostream &out, const alt_bn128_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, alt_bn128_ate_G2_precomp &prec_Q) |
| alt_bn128_Fq12 | alt_bn128_final_exponentiation_first_chunk (const alt_bn128_Fq12 &elt) |
| alt_bn128_Fq12 | alt_bn128_exp_by_neg_z (const alt_bn128_Fq12 &elt) |
| alt_bn128_Fq12 | alt_bn128_final_exponentiation_last_chunk (const alt_bn128_Fq12 &elt) |
| alt_bn128_GT | alt_bn128_final_exponentiation (const alt_bn128_Fq12 &elt) |
| void | doubling_step_for_flipped_miller_loop (const alt_bn128_Fq two_inv, alt_bn128_G2 ¤t, alt_bn128_ate_ell_coeffs &c) |
| void | mixed_addition_step_for_flipped_miller_loop (const alt_bn128_G2 base, alt_bn128_G2 ¤t, alt_bn128_ate_ell_coeffs &c) |
| alt_bn128_ate_G1_precomp | alt_bn128_ate_precompute_G1 (const alt_bn128_G1 &P) |
| alt_bn128_ate_G2_precomp | alt_bn128_ate_precompute_G2 (const alt_bn128_G2 &Q) |
| alt_bn128_Fq12 | alt_bn128_ate_miller_loop (const alt_bn128_ate_G1_precomp &prec_P, const alt_bn128_ate_G2_precomp &prec_Q) |
| alt_bn128_Fq12 | alt_bn128_ate_double_miller_loop (const alt_bn128_ate_G1_precomp &prec_P1, const alt_bn128_ate_G2_precomp &prec_Q1, const alt_bn128_ate_G1_precomp &prec_P2, const alt_bn128_ate_G2_precomp &prec_Q2) |
| alt_bn128_Fq12 | alt_bn128_ate_pairing (const alt_bn128_G1 &P, const alt_bn128_G2 &Q) |
| alt_bn128_GT | alt_bn128_ate_reduced_pairing (const alt_bn128_G1 &P, const alt_bn128_G2 &Q) |
| alt_bn128_G1_precomp | alt_bn128_precompute_G1 (const alt_bn128_G1 &P) |
| alt_bn128_G2_precomp | alt_bn128_precompute_G2 (const alt_bn128_G2 &Q) |
| alt_bn128_Fq12 | alt_bn128_miller_loop (const alt_bn128_G1_precomp &prec_P, const alt_bn128_G2_precomp &prec_Q) |
| alt_bn128_Fq12 | alt_bn128_double_miller_loop (const alt_bn128_G1_precomp &prec_P1, const alt_bn128_G2_precomp &prec_Q1, const alt_bn128_G1_precomp &prec_P2, const alt_bn128_G2_precomp &prec_Q2) |
| alt_bn128_Fq12 | alt_bn128_pairing (const alt_bn128_G1 &P, const alt_bn128_G2 &Q) |
| alt_bn128_GT | alt_bn128_reduced_pairing (const alt_bn128_G1 &P, const alt_bn128_G2 &Q) |
| alt_bn128_GT | alt_bn128_affine_reduced_pairing (const alt_bn128_G1 &P, const alt_bn128_G2 &Q) |
| std::ostream & | operator<< (std::ostream &out, const bls12_377_G1 &g) |
| std::istream & | operator>> (std::istream &in, bls12_377_G1 &g) |
| template<mp_size_t m> | |
| bls12_377_G1 | operator* (const bigint< m > &lhs, const bls12_377_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bls12_377_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const bls12_377_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const bls12_377_G2 &g) |
| std::istream & | operator>> (std::istream &in, bls12_377_G2 &g) |
| template<mp_size_t m> | |
| bls12_377_G2 | operator* (const bigint< m > &lhs, const bls12_377_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bls12_377_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const bls12_377_G2 &rhs) |
| void | init_bls12_377_params () |
| std::ostream & | operator<< (std::ostream &out, const bls12_377_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, bls12_377_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const bls12_377_ate_ell_coeffs &c) |
| std::istream & | operator>> (std::istream &in, bls12_377_ate_ell_coeffs &c) |
| std::ostream & | operator<< (std::ostream &out, const bls12_377_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, bls12_377_ate_G2_precomp &prec_Q) |
| bls12_377_Fq12 | bls12_377_final_exponentiation_first_chunk (const bls12_377_Fq12 &elt) |
| bls12_377_Fq12 | bls12_377_exp_by_z (const bls12_377_Fq12 &elt) |
| bls12_377_Fq12 | bls12_377_final_exponentiation_last_chunk (const bls12_377_Fq12 &elt) |
| bls12_377_GT | bls12_377_final_exponentiation (const bls12_377_Fq12 &elt) |
| void | bls12_377_doubling_step_for_miller_loop (const bls12_377_Fq two_inv, bls12_377_G2 ¤t, bls12_377_ate_ell_coeffs &c) |
| void | bls12_377_mixed_addition_step_for_miller_loop (const bls12_377_G2 &base, bls12_377_G2 ¤t, bls12_377_ate_ell_coeffs &c) |
| bls12_377_ate_G1_precomp | bls12_377_ate_precompute_G1 (const bls12_377_G1 &P) |
| bls12_377_ate_G2_precomp | bls12_377_ate_precompute_G2 (const bls12_377_G2 &Q) |
| bls12_377_Fq12 | bls12_377_ate_miller_loop (const bls12_377_ate_G1_precomp &prec_P, const bls12_377_ate_G2_precomp &prec_Q) |
| bls12_377_Fq12 | bls12_377_ate_double_miller_loop (const bls12_377_ate_G1_precomp &prec_P1, const bls12_377_ate_G2_precomp &prec_Q1, const bls12_377_ate_G1_precomp &prec_P2, const bls12_377_ate_G2_precomp &prec_Q2) |
| bls12_377_Fq12 | bls12_377_ate_pairing (const bls12_377_G1 &P, const bls12_377_G2 &Q) |
| bls12_377_GT | bls12_377_ate_reduced_pairing (const bls12_377_G1 &P, const bls12_377_G2 &Q) |
| bls12_377_G1_precomp | bls12_377_precompute_G1 (const bls12_377_G1 &P) |
| bls12_377_G2_precomp | bls12_377_precompute_G2 (const bls12_377_G2 &Q) |
| bls12_377_Fq12 | bls12_377_miller_loop (const bls12_377_G1_precomp &prec_P, const bls12_377_G2_precomp &prec_Q) |
| bls12_377_Fq12 | bls12_377_double_miller_loop (const bls12_377_G1_precomp &prec_P1, const bls12_377_G2_precomp &prec_Q1, const bls12_377_G1_precomp &prec_P2, const bls12_377_G2_precomp &prec_Q2) |
| bls12_377_Fq12 | bls12_377_pairing (const bls12_377_G1 &P, const bls12_377_G2 &Q) |
| bls12_377_GT | bls12_377_reduced_pairing (const bls12_377_G1 &P, const bls12_377_G2 &Q) |
| bls12_377_GT | bls12_377_affine_reduced_pairing (const bls12_377_G1 &P, const bls12_377_G2 &Q) |
| std::ostream & | operator<< (std::ostream &out, const bls12_381_G1 &g) |
| std::istream & | operator>> (std::istream &in, bls12_381_G1 &g) |
| template<mp_size_t m> | |
| bls12_381_G1 | operator* (const bigint< m > &lhs, const bls12_381_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bls12_381_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const bls12_381_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const bls12_381_G2 &g) |
| std::istream & | operator>> (std::istream &in, bls12_381_G2 &g) |
| template<mp_size_t m> | |
| bls12_381_G2 | operator* (const bigint< m > &lhs, const bls12_381_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bls12_381_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const bls12_381_G2 &rhs) |
| void | init_bls12_381_params () |
| std::ostream & | operator<< (std::ostream &out, const bls12_381_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, bls12_381_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const bls12_381_ate_ell_coeffs &c) |
| std::istream & | operator>> (std::istream &in, bls12_381_ate_ell_coeffs &c) |
| std::ostream & | operator<< (std::ostream &out, const bls12_381_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, bls12_381_ate_G2_precomp &prec_Q) |
| bls12_381_Fq12 | bls12_381_final_exponentiation_first_chunk (const bls12_381_Fq12 &elt) |
| bls12_381_Fq12 | bls12_381_exp_by_z (const bls12_381_Fq12 &elt) |
| bls12_381_Fq12 | bls12_381_final_exponentiation_last_chunk (const bls12_381_Fq12 &elt) |
| bls12_381_GT | bls12_381_final_exponentiation (const bls12_381_Fq12 &elt) |
| void | bls12_381_doubling_step_for_miller_loop (const bls12_381_Fq two_inv, bls12_381_G2 ¤t, bls12_381_ate_ell_coeffs &c) |
| void | bls12_381_mixed_addition_step_for_miller_loop (const bls12_381_G2 base, bls12_381_G2 ¤t, bls12_381_ate_ell_coeffs &c) |
| bls12_381_ate_G1_precomp | bls12_381_ate_precompute_G1 (const bls12_381_G1 &P) |
| bls12_381_ate_G2_precomp | bls12_381_ate_precompute_G2 (const bls12_381_G2 &Q) |
| bls12_381_Fq12 | bls12_381_ate_miller_loop (const bls12_381_ate_G1_precomp &prec_P, const bls12_381_ate_G2_precomp &prec_Q) |
| bls12_381_Fq12 | bls12_381_ate_double_miller_loop (const bls12_381_ate_G1_precomp &prec_P1, const bls12_381_ate_G2_precomp &prec_Q1, const bls12_381_ate_G1_precomp &prec_P2, const bls12_381_ate_G2_precomp &prec_Q2) |
| bls12_381_Fq12 | bls12_381_ate_pairing (const bls12_381_G1 &P, const bls12_381_G2 &Q) |
| bls12_381_GT | bls12_381_ate_reduced_pairing (const bls12_381_G1 &P, const bls12_381_G2 &Q) |
| bls12_381_G1_precomp | bls12_381_precompute_G1 (const bls12_381_G1 &P) |
| bls12_381_G2_precomp | bls12_381_precompute_G2 (const bls12_381_G2 &Q) |
| bls12_381_Fq12 | bls12_381_miller_loop (const bls12_381_G1_precomp &prec_P, const bls12_381_G2_precomp &prec_Q) |
| bls12_381_Fq12 | bls12_381_double_miller_loop (const bls12_381_G1_precomp &prec_P1, const bls12_381_G2_precomp &prec_Q1, const bls12_381_G1_precomp &prec_P2, const bls12_381_G2_precomp &prec_Q2) |
| bls12_381_Fq12 | bls12_381_pairing (const bls12_381_G1 &P, const bls12_381_G2 &Q) |
| bls12_381_GT | bls12_381_reduced_pairing (const bls12_381_G1 &P, const bls12_381_G2 &Q) |
| bls12_381_GT | bls12_381_affine_reduced_pairing (const bls12_381_G1 &P, const bls12_381_G2 &Q) |
| std::ostream & | operator<< (std::ostream &out, const bn128_G1 &g) |
| std::istream & | operator>> (std::istream &in, bn128_G1 &g) |
| template<mp_size_t m> | |
| bn128_G1 | operator* (const bigint< m > &lhs, const bn128_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bn128_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const bn128_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const bn128_G2 &g) |
| std::istream & | operator>> (std::istream &in, bn128_G2 &g) |
| template<mp_size_t m> | |
| bn128_G2 | operator* (const bigint< m > &lhs, const bn128_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bn128_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const bn128_G2 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const bn128_GT &g) |
| std::istream & | operator>> (std::istream &in, bn128_GT &g) |
| template<mp_size_t m> | |
| bn128_GT | operator^ (const bn128_GT &rhs, const bigint< m > &lhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bn128_GT | operator^ (const bn128_GT &rhs, const Fp_model< m, modulus_p > &lhs) |
| void | init_bn128_params () |
| std::ostream & | operator<< (std::ostream &out, const bn128_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, bn128_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const bn128_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, bn128_ate_G2_precomp &prec_Q) |
| bn128_ate_G1_precomp | bn128_ate_precompute_G1 (const bn128_G1 &P) |
| bn128_ate_G2_precomp | bn128_ate_precompute_G2 (const bn128_G2 &Q) |
| bn128_Fq12 | bn128_ate_miller_loop (const bn128_ate_G1_precomp &prec_P, const bn128_ate_G2_precomp &prec_Q) |
| bn128_Fq12 | bn128_double_ate_miller_loop (const bn128_ate_G1_precomp &prec_P1, const bn128_ate_G2_precomp &prec_Q1, const bn128_ate_G1_precomp &prec_P2, const bn128_ate_G2_precomp &prec_Q2) |
| bn128_GT | bn128_final_exponentiation (const bn128_Fq12 &elt) |
| template<typename FieldT > | |
| void | bn_batch_invert (std::vector< FieldT > &vec) |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_G1 &g) |
| std::istream & | operator>> (std::istream &in, bw6_761_G1 &g) |
| template<mp_size_t m> | |
| bw6_761_G1 | operator* (const bigint< m > &lhs, const bw6_761_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bw6_761_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const bw6_761_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_G2 &g) |
| std::istream & | operator>> (std::istream &in, bw6_761_G2 &g) |
| template<mp_size_t m> | |
| bw6_761_G2 | operator* (const bigint< m > &lhs, const bw6_761_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| bw6_761_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const bw6_761_G2 &rhs) |
| void | init_bw6_761_params () |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, bw6_761_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_ate_ell_coeffs &c) |
| std::istream & | operator>> (std::istream &in, bw6_761_ate_ell_coeffs &c) |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_ate_G2_precomp_iteration &prec_Q) |
| std::istream & | operator>> (std::istream &in, bw6_761_ate_G2_precomp_iteration &prec_Q) |
| std::ostream & | operator<< (std::ostream &out, const bw6_761_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, bw6_761_ate_G2_precomp &prec_Q) |
| bw6_761_Fq6 | bw6_761_final_exponentiation_first_chunk (const bw6_761_Fq6 &elt) |
| bw6_761_Fq6 | bw6_761_exp_by_z (const bw6_761_Fq6 &elt) |
| bw6_761_Fq6 | bw6_761_final_exponentiation_last_chunk (const bw6_761_Fq6 &elt) |
| bw6_761_GT | bw6_761_final_exponentiation (const bw6_761_Fq6 &elt) |
| void | doubling_step_for_miller_loop (bw6_761_G2 ¤t, bw6_761_ate_ell_coeffs &c) |
| void | mixed_addition_step_for_miller_loop (const bw6_761_G2 base, bw6_761_G2 ¤t, bw6_761_ate_ell_coeffs &c) |
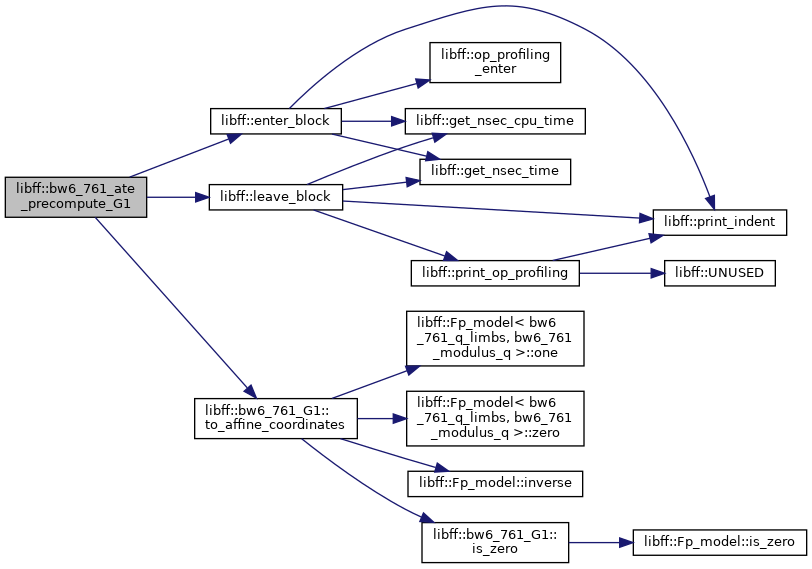
| bw6_761_ate_G1_precomp | bw6_761_ate_precompute_G1 (const bw6_761_G1 &P) |
| bw6_761_ate_G2_precomp | bw6_761_ate_precompute_G2 (const bw6_761_G2 &Q) |
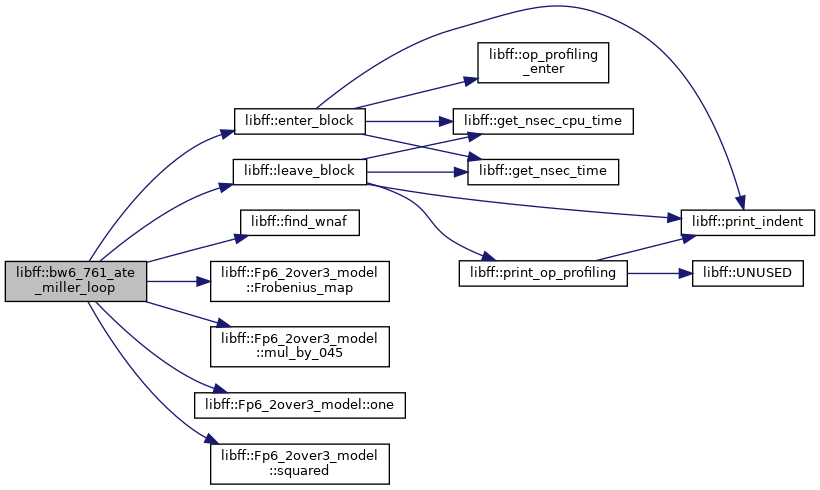
| bw6_761_Fq6 | bw6_761_ate_miller_loop (const bw6_761_ate_G1_precomp &prec_P, const bw6_761_ate_G2_precomp &prec_Q) |
| bw6_761_Fq6 | bw6_761_ate_double_miller_loop (const bw6_761_ate_G1_precomp &prec_P1, const bw6_761_ate_G2_precomp &prec_Q1, const bw6_761_ate_G1_precomp &prec_P2, const bw6_761_ate_G2_precomp &prec_Q2) |
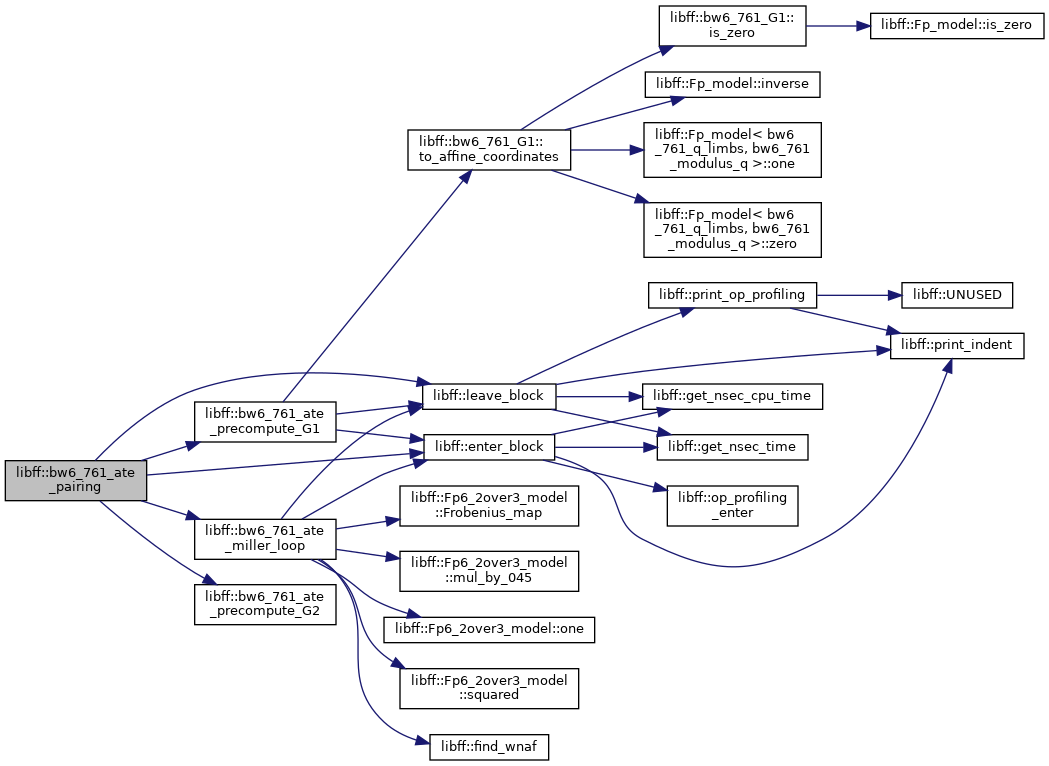
| bw6_761_Fq6 | bw6_761_ate_pairing (const bw6_761_G1 &P, const bw6_761_G2 &Q) |
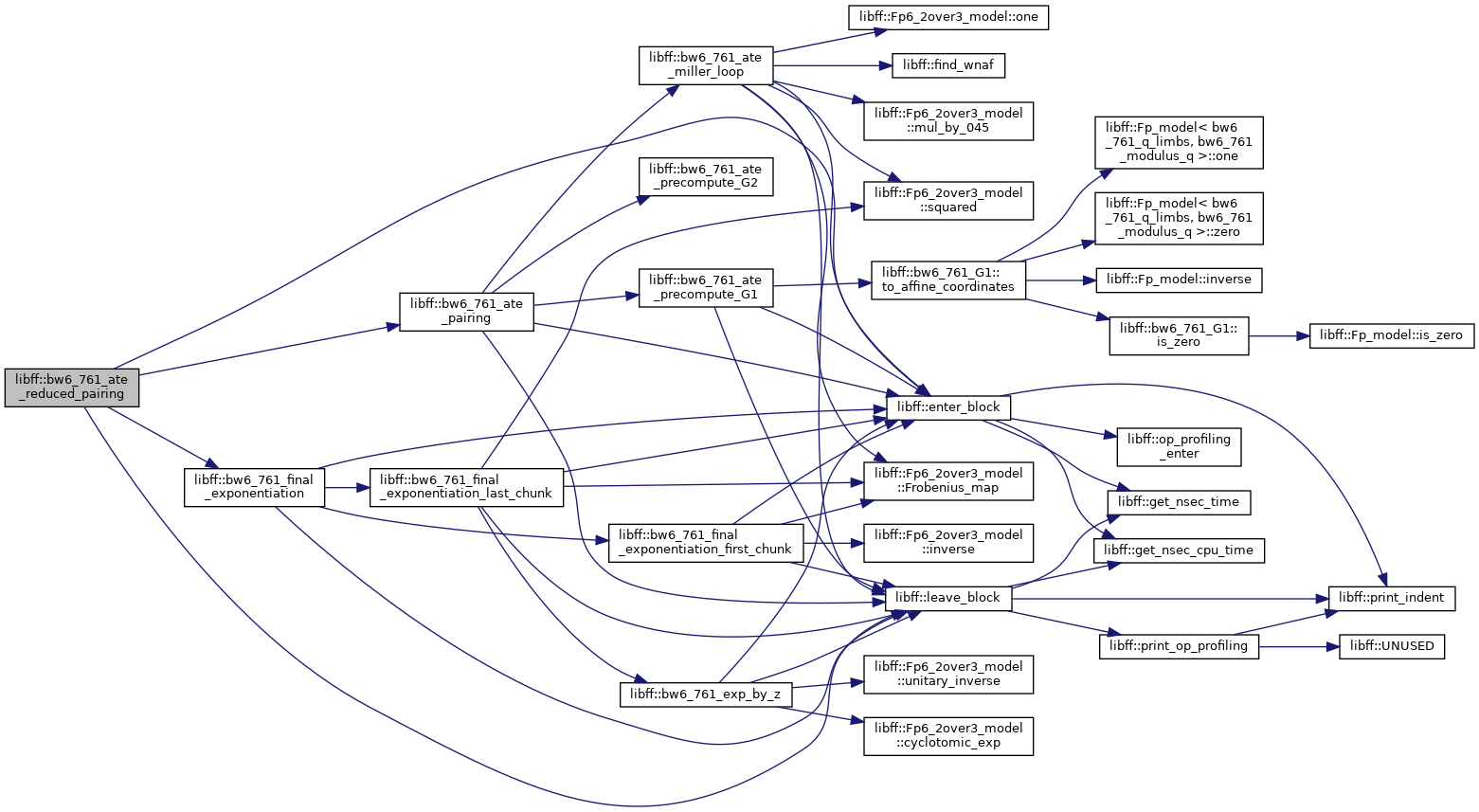
| bw6_761_GT | bw6_761_ate_reduced_pairing (const bw6_761_G1 &P, const bw6_761_G2 &Q) |
| bw6_761_G1_precomp | bw6_761_precompute_G1 (const bw6_761_G1 &P) |
| bw6_761_G2_precomp | bw6_761_precompute_G2 (const bw6_761_G2 &Q) |
| bw6_761_Fq6 | bw6_761_miller_loop (const bw6_761_G1_precomp &prec_P, const bw6_761_G2_precomp &prec_Q) |
| bw6_761_Fq6 | bw6_761_double_miller_loop (const bw6_761_ate_G1_precomp &prec_P1, const bw6_761_ate_G2_precomp &prec_Q1, const bw6_761_ate_G1_precomp &prec_P2, const bw6_761_ate_G2_precomp &prec_Q2) |
| bw6_761_Fq6 | bw6_761_pairing (const bw6_761_G1 &P, const bw6_761_G2 &Q) |
| bw6_761_GT | bw6_761_reduced_pairing (const bw6_761_G1 &P, const bw6_761_G2 &Q) |
| template<encoding_t Enc, form_t Form, compression_t Comp, typename GroupT > | |
| void | group_read (GroupT &v, std::istream &in_s) |
| template<encoding_t Enc, form_t Form, compression_t Comp, typename GroupT > | |
| void | group_write (const GroupT &v, std::ostream &out_s) |
| template<typename GroupT , mp_size_t m> | |
| GroupT | scalar_mul (const GroupT &base, const bigint< m > &scalar) |
| template<typename GroupT > | |
| GroupT | g1_curve_point_at_x (const typename GroupT::base_field &x) |
| template<typename GroupT > | |
| GroupT | g2_curve_point_at_x (const typename GroupT::twist_field &x) |
| std::ostream & | operator<< (std::ostream &out, const edwards_G1 &g) |
| std::istream & | operator>> (std::istream &in, edwards_G1 &g) |
| template<mp_size_t m> | |
| edwards_G1 | operator* (const bigint< m > &lhs, const edwards_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| edwards_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const edwards_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const edwards_G2 &g) |
| std::istream & | operator>> (std::istream &in, edwards_G2 &g) |
| template<mp_size_t m> | |
| edwards_G2 | operator* (const bigint< m > &lhs, const edwards_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| edwards_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const edwards_G2 &rhs) |
| void | init_edwards_params () |
| std::ostream & | operator<< (std::ostream &out, const edwards_Fq_conic_coefficients &cc) |
| std::istream & | operator>> (std::istream &in, edwards_Fq_conic_coefficients &cc) |
| std::ostream & | operator<< (std::ostream &out, const edwards_tate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, edwards_tate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const edwards_tate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, edwards_tate_G2_precomp &prec_Q) |
| std::ostream & | operator<< (std::ostream &out, const edwards_Fq3_conic_coefficients &cc) |
| std::istream & | operator>> (std::istream &in, edwards_Fq3_conic_coefficients &cc) |
| std::ostream & | operator<< (std::ostream &out, const edwards_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, edwards_ate_G2_precomp &prec_Q) |
| std::ostream & | operator<< (std::ostream &out, const edwards_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, edwards_ate_G1_precomp &prec_P) |
| edwards_Fq6 | edwards_final_exponentiation_last_chunk (const edwards_Fq6 &elt, const edwards_Fq6 &elt_inv) |
| edwards_Fq6 | edwards_final_exponentiation_first_chunk (const edwards_Fq6 &elt, const edwards_Fq6 &elt_inv) |
| edwards_GT | edwards_final_exponentiation (const edwards_Fq6 &elt) |
| edwards_tate_G2_precomp | edwards_tate_precompute_G2 (const edwards_G2 &Q) |
| void | doubling_step_for_miller_loop (extended_edwards_G1_projective ¤t, edwards_Fq_conic_coefficients &cc) |
| void | full_addition_step_for_miller_loop (const extended_edwards_G1_projective &base, extended_edwards_G1_projective ¤t, edwards_Fq_conic_coefficients &cc) |
| void | mixed_addition_step_for_miller_loop (const extended_edwards_G1_projective &base, extended_edwards_G1_projective ¤t, edwards_Fq_conic_coefficients &cc) |
| edwards_tate_G1_precomp | edwards_tate_precompute_G1 (const edwards_G1 &P) |
| edwards_Fq6 | edwards_tate_miller_loop (const edwards_tate_G1_precomp &prec_P, const edwards_tate_G2_precomp &prec_Q) |
| edwards_Fq6 | edwards_tate_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| edwards_GT | edwards_tate_reduced_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| void | doubling_step_for_flipped_miller_loop (extended_edwards_G2_projective ¤t, edwards_Fq3_conic_coefficients &cc) |
| void | full_addition_step_for_flipped_miller_loop (const extended_edwards_G2_projective &base, extended_edwards_G2_projective ¤t, edwards_Fq3_conic_coefficients &cc) |
| void | mixed_addition_step_for_flipped_miller_loop (const extended_edwards_G2_projective &base, extended_edwards_G2_projective ¤t, edwards_Fq3_conic_coefficients &cc) |
| edwards_ate_G1_precomp | edwards_ate_precompute_G1 (const edwards_G1 &P) |
| edwards_ate_G2_precomp | edwards_ate_precompute_G2 (const edwards_G2 &Q) |
| edwards_Fq6 | edwards_ate_miller_loop (const edwards_ate_G1_precomp &prec_P, const edwards_ate_G2_precomp &prec_Q) |
| edwards_Fq6 | edwards_ate_double_miller_loop (const edwards_ate_G1_precomp &prec_P1, const edwards_ate_G2_precomp &prec_Q1, const edwards_ate_G1_precomp &prec_P2, const edwards_ate_G2_precomp &prec_Q2) |
| edwards_Fq6 | edwards_ate_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| edwards_GT | edwards_ate_reduced_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| edwards_G1_precomp | edwards_precompute_G1 (const edwards_G1 &P) |
| edwards_G2_precomp | edwards_precompute_G2 (const edwards_G2 &Q) |
| edwards_Fq6 | edwards_miller_loop (const edwards_G1_precomp &prec_P, const edwards_G2_precomp &prec_Q) |
| edwards_Fq6 | edwards_double_miller_loop (const edwards_G1_precomp &prec_P1, const edwards_G2_precomp &prec_Q1, const edwards_G1_precomp &prec_P2, const edwards_G2_precomp &prec_Q2) |
| edwards_Fq6 | edwards_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| edwards_GT | edwards_reduced_pairing (const edwards_G1 &P, const edwards_G2 &Q) |
| std::ostream & | operator<< (std::ostream &out, const mnt4_G1 &g) |
| std::istream & | operator>> (std::istream &in, mnt4_G1 &g) |
| template<mp_size_t m> | |
| mnt4_G1 | operator* (const bigint< m > &lhs, const mnt4_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| mnt4_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const mnt4_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const mnt4_G2 &g) |
| std::istream & | operator>> (std::istream &in, mnt4_G2 &g) |
| template<mp_size_t m> | |
| mnt4_G2 | operator* (const bigint< m > &lhs, const mnt4_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| mnt4_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const mnt4_G2 &rhs) |
| void | init_mnt4_params () |
| std::ostream & | operator<< (std::ostream &out, const mnt4_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, mnt4_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const mnt4_ate_dbl_coeffs &dc) |
| std::istream & | operator>> (std::istream &in, mnt4_ate_dbl_coeffs &dc) |
| std::ostream & | operator<< (std::ostream &out, const mnt4_ate_add_coeffs &ac) |
| std::istream & | operator>> (std::istream &in, mnt4_ate_add_coeffs &ac) |
| std::ostream & | operator<< (std::ostream &out, const mnt4_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, mnt4_ate_G2_precomp &prec_Q) |
| mnt4_Fq4 | mnt4_final_exponentiation_last_chunk (const mnt4_Fq4 &elt, const mnt4_Fq4 &elt_inv) |
| mnt4_Fq4 | mnt4_final_exponentiation_first_chunk (const mnt4_Fq4 &elt, const mnt4_Fq4 &elt_inv) |
| mnt4_GT | mnt4_final_exponentiation (const mnt4_Fq4 &elt) |
| mnt4_affine_ate_G1_precomputation | mnt4_affine_ate_precompute_G1 (const mnt4_G1 &P) |
| mnt4_affine_ate_G2_precomputation | mnt4_affine_ate_precompute_G2 (const mnt4_G2 &Q) |
| mnt4_Fq4 | mnt4_affine_ate_miller_loop (const mnt4_affine_ate_G1_precomputation &prec_P, const mnt4_affine_ate_G2_precomputation &prec_Q) |
| void | doubling_step_for_flipped_miller_loop (extended_mnt4_G2_projective ¤t, mnt4_ate_dbl_coeffs &dc) |
| void | mixed_addition_step_for_flipped_miller_loop (const mnt4_Fq2 base_X, const mnt4_Fq2 base_Y, const mnt4_Fq2 base_Y_squared, extended_mnt4_G2_projective ¤t, mnt4_ate_add_coeffs &ac) |
| mnt4_ate_G1_precomp | mnt4_ate_precompute_G1 (const mnt4_G1 &P) |
| mnt4_ate_G2_precomp | mnt4_ate_precompute_G2 (const mnt4_G2 &Q) |
| mnt4_Fq4 | mnt4_ate_miller_loop (const mnt4_ate_G1_precomp &prec_P, const mnt4_ate_G2_precomp &prec_Q) |
| mnt4_Fq4 | mnt4_ate_double_miller_loop (const mnt4_ate_G1_precomp &prec_P1, const mnt4_ate_G2_precomp &prec_Q1, const mnt4_ate_G1_precomp &prec_P2, const mnt4_ate_G2_precomp &prec_Q2) |
| mnt4_Fq4 | mnt4_ate_pairing (const mnt4_G1 &P, const mnt4_G2 &Q) |
| mnt4_GT | mnt4_ate_reduced_pairing (const mnt4_G1 &P, const mnt4_G2 &Q) |
| mnt4_G1_precomp | mnt4_precompute_G1 (const mnt4_G1 &P) |
| mnt4_G2_precomp | mnt4_precompute_G2 (const mnt4_G2 &Q) |
| mnt4_Fq4 | mnt4_miller_loop (const mnt4_G1_precomp &prec_P, const mnt4_G2_precomp &prec_Q) |
| mnt4_Fq4 | mnt4_double_miller_loop (const mnt4_G1_precomp &prec_P1, const mnt4_G2_precomp &prec_Q1, const mnt4_G1_precomp &prec_P2, const mnt4_G2_precomp &prec_Q2) |
| mnt4_Fq4 | mnt4_pairing (const mnt4_G1 &P, const mnt4_G2 &Q) |
| mnt4_GT | mnt4_reduced_pairing (const mnt4_G1 &P, const mnt4_G2 &Q) |
| mnt4_GT | mnt4_affine_reduced_pairing (const mnt4_G1 &P, const mnt4_G2 &Q) |
| std::ostream & | operator<< (std::ostream &out, const mnt6_G1 &g) |
| std::istream & | operator>> (std::istream &in, mnt6_G1 &g) |
| template<mp_size_t m> | |
| mnt6_G1 | operator* (const bigint< m > &lhs, const mnt6_G1 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| mnt6_G1 | operator* (const Fp_model< m, modulus_p > &lhs, const mnt6_G1 &rhs) |
| std::ostream & | operator<< (std::ostream &out, const mnt6_G2 &g) |
| std::istream & | operator>> (std::istream &in, mnt6_G2 &g) |
| template<mp_size_t m> | |
| mnt6_G2 | operator* (const bigint< m > &lhs, const mnt6_G2 &rhs) |
| template<mp_size_t m, const bigint< m > & modulus_p> | |
| mnt6_G2 | operator* (const Fp_model< m, modulus_p > &lhs, const mnt6_G2 &rhs) |
| void | init_mnt6_params () |
| std::ostream & | operator<< (std::ostream &out, const mnt6_ate_G1_precomp &prec_P) |
| std::istream & | operator>> (std::istream &in, mnt6_ate_G1_precomp &prec_P) |
| std::ostream & | operator<< (std::ostream &out, const mnt6_ate_dbl_coeffs &dc) |
| std::istream & | operator>> (std::istream &in, mnt6_ate_dbl_coeffs &dc) |
| std::ostream & | operator<< (std::ostream &out, const mnt6_ate_add_coeffs &ac) |
| std::istream & | operator>> (std::istream &in, mnt6_ate_add_coeffs &ac) |
| std::ostream & | operator<< (std::ostream &out, const mnt6_ate_G2_precomp &prec_Q) |
| std::istream & | operator>> (std::istream &in, mnt6_ate_G2_precomp &prec_Q) |
| mnt6_Fq6 | mnt6_final_exponentiation_last_chunk (const mnt6_Fq6 &elt, const mnt6_Fq6 &elt_inv) |
| mnt6_Fq6 | mnt6_final_exponentiation_first_chunk (const mnt6_Fq6 &elt, const mnt6_Fq6 &elt_inv) |
| mnt6_GT | mnt6_final_exponentiation (const mnt6_Fq6 &elt) |
| mnt6_affine_ate_G1_precomputation | mnt6_affine_ate_precompute_G1 (const mnt6_G1 &P) |
| mnt6_affine_ate_G2_precomputation | mnt6_affine_ate_precompute_G2 (const mnt6_G2 &Q) |
| mnt6_Fq6 | mnt6_affine_ate_miller_loop (const mnt6_affine_ate_G1_precomputation &prec_P, const mnt6_affine_ate_G2_precomputation &prec_Q) |
| void | doubling_step_for_flipped_miller_loop (extended_mnt6_G2_projective ¤t, mnt6_ate_dbl_coeffs &dc) |
| void | mixed_addition_step_for_flipped_miller_loop (const mnt6_Fq3 base_X, const mnt6_Fq3 base_Y, const mnt6_Fq3 base_Y_squared, extended_mnt6_G2_projective ¤t, mnt6_ate_add_coeffs &ac) |
| mnt6_ate_G1_precomp | mnt6_ate_precompute_G1 (const mnt6_G1 &P) |
| mnt6_ate_G2_precomp | mnt6_ate_precompute_G2 (const mnt6_G2 &Q) |
| mnt6_Fq6 | mnt6_ate_miller_loop (const mnt6_ate_G1_precomp &prec_P, const mnt6_ate_G2_precomp &prec_Q) |
| mnt6_Fq6 | mnt6_ate_double_miller_loop (const mnt6_ate_G1_precomp &prec_P1, const mnt6_ate_G2_precomp &prec_Q1, const mnt6_ate_G1_precomp &prec_P2, const mnt6_ate_G2_precomp &prec_Q2) |
| mnt6_Fq6 | mnt6_ate_pairing (const mnt6_G1 &P, const mnt6_G2 &Q) |
| mnt6_GT | mnt6_ate_reduced_pairing (const mnt6_G1 &P, const mnt6_G2 &Q) |
| mnt6_G1_precomp | mnt6_precompute_G1 (const mnt6_G1 &P) |
| mnt6_G2_precomp | mnt6_precompute_G2 (const mnt6_G2 &Q) |
| mnt6_Fq6 | mnt6_miller_loop (const mnt6_G1_precomp &prec_P, const mnt6_G2_precomp &prec_Q) |
| mnt6_Fq6 | mnt6_double_miller_loop (const mnt6_G1_precomp &prec_P1, const mnt6_G2_precomp &prec_Q1, const mnt6_G1_precomp &prec_P2, const mnt6_G2_precomp &prec_Q2) |
| mnt6_Fq6 | mnt6_pairing (const mnt6_G1 &P, const mnt6_G2 &Q) |
| mnt6_GT | mnt6_reduced_pairing (const mnt6_G1 &P, const mnt6_G2 &Q) |
| mnt6_GT | mnt6_affine_reduced_pairing (const mnt6_G1 &P, const mnt6_G2 &Q) |
| template<typename FieldT , mp_size_t m> | |
| FieldT | power (const FieldT &base, const bigint< m > &exponent) |
| template<typename FieldT > | |
| FieldT | power (const FieldT &base, const unsigned long exponent) |
| template<mp_size_t n> | |
| std::ostream & | operator<< (std::ostream &, const bigint< n > &) |
| template<mp_size_t n> | |
| std::istream & | operator>> (std::istream &, bigint< n > &) |
| template<typename BigIntT > | |
| void | bigint_from_hex (BigIntT &v, const std::string &hex) |
| template<typename BigIntT > | |
| std::string | bigint_to_hex (const BigIntT &v, bool prefix=false) |
| template<encoding_t Enc = encoding_binary, form_t Form = form_plain, typename FieldT > | |
| void | field_read (FieldT &v, std::istream &in_s) |
| template<encoding_t Enc = encoding_binary, form_t Form = form_plain, typename FieldT > | |
| void | field_write (const FieldT &v, std::ostream &out_s) |
| template<typename FieldT > | |
| std::enable_if< std::is_same< FieldT, Double >::value, bool >::type | has_root_of_unity (const size_t n) |
| template<typename FieldT > | |
| std::enable_if<!std::is_same< FieldT, Double >::value, bool >::type | has_root_of_unity (const size_t n) |
| template<typename FieldT > | |
| std::enable_if< std::is_same< FieldT, Double >::value, FieldT >::type | get_root_of_unity (const size_t n) |
| template<typename FieldT > | |
| std::enable_if<!std::is_same< FieldT, Double >::value, FieldT >::type | get_root_of_unity (const size_t n) |
| template<mp_size_t n> | |
| size_t | field_get_digit (const bigint< n > &v, const size_t digit_size, const size_t digit_index) |
| Decompose v into fixed-size digits of digit_size bits each. More... | |
| template<mp_size_t n> | |
| ssize_t | field_get_signed_digit (const bigint< n > &v, const size_t digit_size, const size_t digit_index) |
| Decompose v into fixed-size signed digits of digit_size bits each. More... | |
| template<typename FieldT > | |
| void | field_get_signed_digits (std::vector< ssize_t > &digits, const FieldT &v, const size_t digit_size, const size_t num_digits) |
| template<typename FieldT > | |
| std::vector< FieldT > | pack_int_vector_into_field_element_vector (const std::vector< size_t > &v, const size_t w) |
| template<typename FieldT > | |
| std::vector< FieldT > | pack_bit_vector_into_field_element_vector (const bit_vector &v, const size_t chunk_bits) |
| template<typename FieldT > | |
| std::vector< FieldT > | pack_bit_vector_into_field_element_vector (const bit_vector &v) |
| template<typename FieldT > | |
| std::vector< FieldT > | convert_bit_vector_to_field_element_vector (const bit_vector &v) |
| template<typename FieldT > | |
| bit_vector | convert_field_element_vector_to_bit_vector (const std::vector< FieldT > &v) |
| template<typename FieldT > | |
| bit_vector | convert_field_element_to_bit_vector (const FieldT &el) |
| template<typename FieldT > | |
| bit_vector | convert_field_element_to_bit_vector (const FieldT &el, const size_t bitcount) |
| template<typename FieldT > | |
| FieldT | convert_bit_vector_to_field_element (const bit_vector &v) |
| template<typename FieldT > | |
| void | batch_invert (std::vector< FieldT > &vec) |
| template<typename FieldT > | |
| const FieldT::my_Fp & | field_get_component_0 (const FieldT &v) |
| template<mp_size_t wn, const bigint< wn > & wmodulus, mp_size_t nn, const bigint< nn > & nmodulus> | |
| void | fp_from_fp (Fp_model< wn, wmodulus > &wfp, const Fp_model< nn, nmodulus > &nfp) |
| template<typename FieldT > | |
| void | print_vector (const std::vector< FieldT > &v) |
| print the elements of a vector More... | |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp12_2over3over2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp12_2over3over2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< Fp12_2over3over2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &in, std::vector< Fp12_2over3over2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp12_2over3over2_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp12_2over3over2_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp12_2over3over2_model< n, modulus > | operator* (const Fp2_model< n, modulus > &lhs, const Fp12_2over3over2_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp12_2over3over2_model< n, modulus > | operator* (const Fp6_3over2_model< n, modulus > &lhs, const Fp12_2over3over2_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m> | |
| Fp12_2over3over2_model< n, modulus > | operator^ (const Fp12_2over3over2_model< n, modulus > &self, const bigint< m > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m, const bigint< m > & exp_modulus> | |
| Fp12_2over3over2_model< n, modulus > | operator^ (const Fp12_2over3over2_model< n, modulus > &self, const Fp_model< m, exp_modulus > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< Fp2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &in, std::vector< Fp2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp2_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp2_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp3_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp3_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< Fp3_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &in, std::vector< Fp3_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp3_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp3_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp4_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp4_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp4_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp4_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp4_model< n, modulus > | operator* (const Fp2_model< n, modulus > &lhs, const Fp4_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m> | |
| Fp4_model< n, modulus > | operator^ (const Fp4_model< n, modulus > &self, const bigint< m > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m, const bigint< m > & modulus_p> | |
| Fp4_model< n, modulus > | operator^ (const Fp4_model< n, modulus > &self, const Fp_model< m, modulus_p > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp6_2over3_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp6_2over3_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< Fp6_2over3_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &in, std::vector< Fp6_2over3_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp6_2over3_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp6_2over3_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m> | |
| Fp6_2over3_model< n, modulus > | operator^ (const Fp6_2over3_model< n, modulus > &self, const bigint< m > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus, mp_size_t m, const bigint< m > & exp_modulus> | |
| Fp6_2over3_model< n, modulus > | operator^ (const Fp6_2over3_model< n, modulus > &self, const Fp_model< m, exp_modulus > &exponent) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &, const Fp6_3over2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &, Fp6_3over2_model< n, modulus > &) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< Fp6_3over2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| std::istream & | operator>> (std::istream &in, std::vector< Fp6_3over2_model< n, modulus >> &v) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp6_3over2_model< n, modulus > | operator* (const Fp_model< n, modulus > &lhs, const Fp6_3over2_model< n, modulus > &rhs) |
| template<mp_size_t n, const bigint< n > & modulus> | |
| Fp6_3over2_model< n, modulus > | operator* (const Fp2_model< n, modulus > &lhs, const Fp6_3over2_model< n, modulus > &rhs) |
| template<typename T , typename FieldT , multi_exp_method Method, multi_exp_base_form BaseForm = multi_exp_base_form_normal> | |
| T | multi_exp (typename std::vector< T >::const_iterator vec_start, typename std::vector< T >::const_iterator vec_end, typename std::vector< FieldT >::const_iterator scalar_start, typename std::vector< FieldT >::const_iterator scalar_end, const size_t chunks) |
| template<typename T , typename FieldT , multi_exp_method Method, multi_exp_base_form BaseForm = multi_exp_base_form_normal> | |
| T | multi_exp_filter_one_zero (typename std::vector< T >::const_iterator vec_start, typename std::vector< T >::const_iterator vec_end, typename std::vector< FieldT >::const_iterator scalar_start, typename std::vector< FieldT >::const_iterator scalar_end, const size_t chunks) |
| template<typename T > | |
| T | inner_product (typename std::vector< T >::const_iterator a_start, typename std::vector< T >::const_iterator a_end, typename std::vector< T >::const_iterator b_start, typename std::vector< T >::const_iterator b_end) |
| template<typename T > | |
| size_t | get_exp_window_size (const size_t num_scalars) |
| Compute window size for the given number of scalars. More... | |
| template<typename T > | |
| window_table< T > | get_window_table (const size_t scalar_size, const size_t window, const T &g) |
| Compute table of window sizes. More... | |
| template<typename T , typename FieldT > | |
| T | windowed_exp (const size_t scalar_size, const size_t window, const window_table< T > &powers_of_g, const FieldT &pow) |
| template<typename T , typename FieldT > | |
| std::vector< T > | batch_exp (const size_t scalar_size, const size_t window, const window_table< T > &table, const std::vector< FieldT > &v) |
| template<typename T , typename FieldT > | |
| std::vector< T > | batch_exp (const size_t scalar_size, const size_t window, const window_table< T > &table, const std::vector< FieldT > &v, size_t num_entries) |
| template<typename T , typename FieldT > | |
| std::vector< T > | batch_exp_with_coeff (const size_t scalar_size, const size_t window, const window_table< T > &table, const FieldT &coeff, const std::vector< FieldT > &v) |
| template<typename T > | |
| void | batch_to_special (std::vector< T > &vec) |
| template<form_t Form, compression_t Comp, typename GroupT , typename FieldT > | |
| GroupT | multi_exp_stream (std::istream &base_elements_in, const std::vector< FieldT > &exponents) |
| template<form_t Form, compression_t Comp, typename GroupT , typename FieldT > | |
| GroupT | multi_exp_stream_with_precompute (std::istream &precomputed_elements_in, const std::vector< FieldT > &exponents, const size_t precompute_c) |
| template<mp_size_t n> | |
| void | update_wnaf (std::vector< long > &naf, const size_t window_size, const bigint< n > &scalar) |
| template<mp_size_t n> | |
| std::vector< long > | find_wnaf (const size_t window_size, const bigint< n > &scalar) |
| template<typename T > | |
| size_t | wnaf_opt_window_size (const size_t scalar_bits) |
| Compute optimal window size. More... | |
| template<typename T > | |
| T | fixed_window_wnaf_exp (const size_t window_size, const T &base, const std::vector< long > &naf) |
| template<typename T , mp_size_t n> | |
| T | fixed_window_wnaf_exp (const size_t window_size, const T &base, const bigint< n > &scalar) |
| template<typename T , mp_size_t n> | |
| T | opt_window_wnaf_exp (const T &base, const bigint< n > &scalar, const size_t scalar_bits) |
| uint8_t | char_to_nibble (const char c) |
| void | hex_to_bytes_reversed (const std::string &hex, void *dest, size_t bytes) |
| std::string | bytes_to_hex_reversed (const void *bytes, size_t num_bytes, bool prefix=false) |
| "prefix" here refers to "0x" More... | |
| long long | get_nsec_time () |
| long long | get_nsec_cpu_time () |
| void | start_profiling () |
| void | clear_profiling_counters () |
| void | print_cumulative_time_entry (const std::string &key, const long long factor) |
| void | print_cumulative_times (const long long factor) |
| void | print_cumulative_op_counts (const bool only_fq) |
| void | print_op_profiling (const std::string &msg) |
| void | print_time (const char *msg) |
| void | print_header (const char *msg) |
| void | print_indent () |
| void | op_profiling_enter (const std::string &msg) |
| void | enter_block (const std::string &msg, const bool indent) |
| void | leave_block (const std::string &msg, const bool indent) |
| void | print_mem (const std::string &s) |
| void | print_compilation_info () |
| template<typename FieldT > | |
| FieldT | SHA512_rng (const uint64_t idx) |
| void | consume_newline (std::istream &in) |
| void | consume_OUTPUT_NEWLINE (std::istream &in) |
| void | consume_OUTPUT_SEPARATOR (std::istream &in) |
| void | output_bool (std::ostream &out, const bool b) |
| void | input_bool (std::istream &in, bool &b) |
| void | output_bool_vector (std::ostream &out, const std::vector< bool > &v) |
| void | input_bool_vector (std::istream &in, std::vector< bool > &v) |
| template<typename T > | |
| T | reserialize (const T &obj) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const std::vector< T > &v) |
| template<typename T > | |
| std::istream & | operator>> (std::ostream &out, std::vector< T > &v) |
| template<typename T1 , typename T2 > | |
| std::ostream & | operator<< (std::ostream &out, const std::map< T1, T2 > &m) |
| template<typename T1 , typename T2 > | |
| std::istream & | operator>> (std::istream &in, std::map< T1, T2 > &m) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const std::set< T > &s) |
| template<typename T > | |
| std::istream & | operator>> (std::istream &in, std::set< T > &s) |
| size_t | get_power_of_two (size_t n) |
| size_t | log2 (size_t n) |
| size_t | to_twos_complement (int i, size_t w) |
| int | from_twos_complement (size_t i, size_t w) |
| size_t | bitreverse (size_t n, const size_t l) |
| bit_vector | int_list_to_bits (const std::initializer_list< unsigned long > &l, const size_t wordsize) |
| long long | div_ceil (long long x, long long y) |
| bool | is_little_endian () |
| std::string | FORMAT (const std::string &prefix, const char *format,...) |
| void | serialize_bit_vector (std::ostream &out, const bit_vector &v) |
| void | deserialize_bit_vector (std::istream &in, bit_vector &v) |
| size_t | exp2 (size_t k) |
| template<typename... Types> | |
| void | UNUSED (Types &&...) |
| A variadic template to suppress unused argument warnings. More... | |
| template<typename T > | |
| size_t | size_in_bits (const std::vector< T > &v) |
Typedef Documentation
◆ affine_ate_G1_precomp
| using libff::affine_ate_G1_precomp = typedef typename EC_ppT::affine_ate_G1_precomp_type |
Definition at line 81 of file public_params.hpp.
◆ affine_ate_G2_precomp
| using libff::affine_ate_G2_precomp = typedef typename EC_ppT::affine_ate_G2_precomp_type |
Definition at line 83 of file public_params.hpp.
◆ alt_bn128_Fq
Definition at line 31 of file alt_bn128_init.hpp.
◆ alt_bn128_Fq12
Definition at line 35 of file alt_bn128_init.hpp.
◆ alt_bn128_Fq2
Definition at line 32 of file alt_bn128_init.hpp.
◆ alt_bn128_Fq6
Definition at line 33 of file alt_bn128_init.hpp.
◆ alt_bn128_Fr
Definition at line 30 of file alt_bn128_init.hpp.
◆ alt_bn128_G1_precomp
Definition at line 76 of file alt_bn128_pairing.hpp.
◆ alt_bn128_G2_precomp
Definition at line 77 of file alt_bn128_pairing.hpp.
◆ alt_bn128_GT
| typedef alt_bn128_Fq12 libff::alt_bn128_GT |
Definition at line 36 of file alt_bn128_init.hpp.
◆ bit_vector
| typedef std::vector<bool> libff::bit_vector |
◆ bls12_377_Fq
Definition at line 48 of file bls12_377_init.hpp.
◆ bls12_377_Fq12
Definition at line 52 of file bls12_377_init.hpp.
◆ bls12_377_Fq2
Definition at line 49 of file bls12_377_init.hpp.
◆ bls12_377_Fq6
Definition at line 50 of file bls12_377_init.hpp.
◆ bls12_377_Fr
Definition at line 47 of file bls12_377_init.hpp.
◆ bls12_377_G1_precomp
Definition at line 91 of file bls12_377_pairing.hpp.
◆ bls12_377_G2_precomp
Definition at line 92 of file bls12_377_pairing.hpp.
◆ bls12_377_GT
| typedef bls12_377_Fq12 libff::bls12_377_GT |
Definition at line 53 of file bls12_377_init.hpp.
◆ bls12_381_Fq
Definition at line 31 of file bls12_381_init.hpp.
◆ bls12_381_Fq12
Definition at line 35 of file bls12_381_init.hpp.
◆ bls12_381_Fq2
Definition at line 32 of file bls12_381_init.hpp.
◆ bls12_381_Fq6
Definition at line 33 of file bls12_381_init.hpp.
◆ bls12_381_Fr
Definition at line 30 of file bls12_381_init.hpp.
◆ bls12_381_G1_precomp
Definition at line 91 of file bls12_381_pairing.hpp.
◆ bls12_381_G2_precomp
Definition at line 92 of file bls12_381_pairing.hpp.
◆ bls12_381_GT
| typedef bls12_381_Fq12 libff::bls12_381_GT |
Definition at line 36 of file bls12_381_init.hpp.
◆ bn128_ate_ell_coeffs
| typedef bn::Fp6 libff::bn128_ate_ell_coeffs |
Definition at line 32 of file bn128_pairing.hpp.
◆ bn128_Fq
| typedef Fp_model<bn128_q_limbs, bn128_modulus_q> libff::bn128_Fq |
Definition at line 40 of file bn128_init.hpp.
◆ bn128_Fq12
| typedef bn128_GT libff::bn128_Fq12 |
Definition at line 46 of file bn128_init.hpp.
◆ bn128_Fr
| typedef Fp_model<bn128_r_limbs, bn128_modulus_r> libff::bn128_Fr |
Definition at line 39 of file bn128_init.hpp.
◆ bw6_761_Fq
Definition at line 24 of file bw6_761_init.hpp.
◆ bw6_761_Fq3
Definition at line 25 of file bw6_761_init.hpp.
◆ bw6_761_Fq6
Definition at line 26 of file bw6_761_init.hpp.
◆ bw6_761_Fr
Definition at line 23 of file bw6_761_init.hpp.
◆ bw6_761_G1_precomp
Definition at line 80 of file bw6_761_pairing.hpp.
◆ bw6_761_G2_precomp
Definition at line 81 of file bw6_761_pairing.hpp.
◆ bw6_761_GT
| typedef bw6_761_Fq6 libff::bw6_761_GT |
Definition at line 27 of file bw6_761_init.hpp.
◆ edwards_ate_G2_precomp
| typedef std::vector<edwards_Fq3_conic_coefficients> libff::edwards_ate_G2_precomp |
Definition at line 77 of file edwards_pairing.hpp.
◆ edwards_Fq
Definition at line 30 of file edwards_init.hpp.
◆ edwards_Fq3
Definition at line 31 of file edwards_init.hpp.
◆ edwards_Fq6
Definition at line 32 of file edwards_init.hpp.
◆ edwards_Fr
Definition at line 29 of file edwards_init.hpp.
◆ edwards_G1_precomp
Definition at line 112 of file edwards_pairing.hpp.
◆ edwards_G2_precomp
Definition at line 113 of file edwards_pairing.hpp.
◆ edwards_GT
| typedef edwards_Fq6 libff::edwards_GT |
Definition at line 33 of file edwards_init.hpp.
◆ edwards_tate_G1_precomp
| typedef std::vector<edwards_Fq_conic_coefficients> libff::edwards_tate_G1_precomp |
Definition at line 37 of file edwards_pairing.hpp.
◆ Fq
| using libff::Fq = typedef typename EC_ppT::Fq_type |
Definition at line 84 of file public_params.hpp.
◆ Fqe
| using libff::Fqe = typedef typename EC_ppT::Fqe_type |
Definition at line 85 of file public_params.hpp.
◆ Fqk
| using libff::Fqk = typedef typename EC_ppT::Fqk_type |
Definition at line 86 of file public_params.hpp.
◆ Fr
| using libff::Fr = typedef typename EC_ppT::Fp_type |
For every curve the user should define corresponding public_params with the following typedefs:
Fp_type G1_type G2_type G1_precomp_type G2_precomp_type affine_ate_G1_precomp_type affine_ate_G2_precomp_type Fq_type Fqe_type Fqk_type GT_type
one should also define the following static elements and methods:
const std::string name;
void init_public_params();
GT<EC_ppT> final_exponentiation(const Fqk<EC_ppT> &elt);
G1_precomp<EC_ppT> precompute_G1(const G1<EC_ppT> &P); G2_precomp<EC_ppT> precompute_G2(const G2<EC_ppT> &Q);
Fqk<EC_ppT> miller_loop( const G1_precomp<EC_ppT> &prec_P, const G2_precomp<EC_ppT> &prec_Q);
affine_ate_G1_precomp<EC_ppT> affine_ate_precompute_G1(const G1<EC_ppT> &P); affine_ate_G2_precomp<EC_ppT> affine_ate_precompute_G2(const G2<EC_ppT> &Q);
Fqk<EC_ppT> affine_ate_miller_loop( const affine_ate_G1_precomp<EC_ppT> &prec_P, const affine_ate_G2_precomp<EC_ppT> &prec_Q); Fqk<EC_ppT> affine_ate_e_over_e_miller_loop( const affine_ate_G1_precomp<EC_ppT> &prec_P1, const affine_ate_G2_precomp<EC_ppT> &prec_Q1, const affine_ate_G1_precomp<EC_ppT> &prec_P2, const affine_ate_G2_precomp<EC_ppT> &prec_Q2); Fqk<EC_ppT> affine_ate_e_times_e_over_e_miller_loop( const affine_ate_G1_precomp<EC_ppT> &prec_P1, const affine_ate_G2_precomp<EC_ppT> &prec_Q1, const affine_ate_G1_precomp<EC_ppT> &prec_P2, const affine_ate_G2_precomp<EC_ppT> &prec_Q2, const affine_ate_G1_precomp<EC_ppT> &prec_P3, const affine_ate_G2_precomp<EC_ppT> &prec_Q3); Fqk<EC_ppT> double_miller_loop( const G1_precomp<EC_ppT> &prec_P1, const G2_precomp<EC_ppT> &prec_Q1, const G1_precomp<EC_ppT> &prec_P2, const G2_precomp<EC_ppT> &prec_Q2);
Fqk<EC_ppT> pairing(const G1<EC_ppT> &P, const G2<EC_ppT> &Q); GT<EC_ppT> reduced_pairing(const G1<EC_ppT> &P, const G2<EC_ppT> &Q); GT<EC_ppT> affine_reduced_pairing(const G1<EC_ppT> &P, const G2<EC_ppT> &Q);
Definition at line 75 of file public_params.hpp.
◆ Fr_vector
| using libff::Fr_vector = typedef std::vector<Fr<EC_ppT> > |
Definition at line 89 of file public_params.hpp.
◆ G1
| using libff::G1 = typedef typename EC_ppT::G1_type |
Definition at line 76 of file public_params.hpp.
◆ G1_precomp
| using libff::G1_precomp = typedef typename EC_ppT::G1_precomp_type |
Definition at line 78 of file public_params.hpp.
◆ G1_vector
| using libff::G1_vector = typedef std::vector<G1<EC_ppT> > |
Definition at line 90 of file public_params.hpp.
◆ G2
| using libff::G2 = typedef typename EC_ppT::G2_type |
Definition at line 77 of file public_params.hpp.
◆ G2_precomp
| using libff::G2_precomp = typedef typename EC_ppT::G2_precomp_type |
Definition at line 79 of file public_params.hpp.
◆ G2_vector
| using libff::G2_vector = typedef std::vector<G2<EC_ppT> > |
Definition at line 91 of file public_params.hpp.
◆ GT
| using libff::GT = typedef typename EC_ppT::GT_type |
Definition at line 87 of file public_params.hpp.
◆ mnt4_Fq
| typedef Fp_model<mnt4_q_limbs, mnt4_modulus_q> libff::mnt4_Fq |
Definition at line 37 of file mnt4_init.hpp.
◆ mnt4_Fq2
| typedef Fp2_model<mnt4_q_limbs, mnt4_modulus_q> libff::mnt4_Fq2 |
Definition at line 38 of file mnt4_init.hpp.
◆ mnt4_Fq4
| typedef Fp4_model<mnt4_q_limbs, mnt4_modulus_q> libff::mnt4_Fq4 |
Definition at line 39 of file mnt4_init.hpp.
◆ mnt4_Fr
| typedef Fp_model<mnt4_r_limbs, mnt4_modulus_r> libff::mnt4_Fr |
Definition at line 36 of file mnt4_init.hpp.
◆ mnt4_G1_precomp
Definition at line 130 of file mnt4_pairing.hpp.
◆ mnt4_G2_precomp
Definition at line 131 of file mnt4_pairing.hpp.
◆ mnt4_GT
| typedef mnt4_Fq4 libff::mnt4_GT |
Definition at line 40 of file mnt4_init.hpp.
◆ mnt6_Fq
| typedef Fp_model<mnt6_q_limbs, mnt6_modulus_q> libff::mnt6_Fq |
Definition at line 37 of file mnt6_init.hpp.
◆ mnt6_Fq3
| typedef Fp3_model<mnt6_q_limbs, mnt6_modulus_q> libff::mnt6_Fq3 |
Definition at line 38 of file mnt6_init.hpp.
◆ mnt6_Fq6
Definition at line 39 of file mnt6_init.hpp.
◆ mnt6_Fr
| typedef Fp_model<mnt6_r_limbs, mnt6_modulus_r> libff::mnt6_Fr |
Definition at line 36 of file mnt6_init.hpp.
◆ mnt6_G1_precomp
Definition at line 130 of file mnt6_pairing.hpp.
◆ mnt6_G2_precomp
Definition at line 131 of file mnt6_pairing.hpp.
◆ mnt6_GT
| typedef mnt6_Fq6 libff::mnt6_GT |
Definition at line 40 of file mnt6_init.hpp.
◆ window_table
| using libff::window_table = typedef std::vector<std::vector<T> > |
A window table stores window sizes for different instance sizes for fixed-base multi-scalar multiplications.
Definition at line 101 of file multiexp.hpp.
Enumeration Type Documentation
◆ compression_t
| enum libff::compression_t : uint8_t |
Enable / disable compression in (de)serialization.
| Enumerator | |
|---|---|
| compression_off | |
| compression_on | |
Definition at line 31 of file serialization.hpp.
◆ encoding_t
| enum libff::encoding_t : uint8_t |
Encodings for (de)serialization.
| Enumerator | |
|---|---|
| encoding_binary | |
| encoding_json | |
Definition at line 19 of file serialization.hpp.
◆ form_t
| enum libff::form_t : uint8_t |
Encodings for (de)serialization.
| Enumerator | |
|---|---|
| form_plain | |
| form_montgomery | |
Definition at line 25 of file serialization.hpp.
◆ multi_exp_base_form
Form of base elements passed to multi_exp routines.
Definition at line 45 of file multiexp.hpp.
◆ multi_exp_method
| Enumerator | |
|---|---|
| multi_exp_method_naive | Naive multi-exponentiation individually multiplies each base by the corresponding scalar and adds up the results. multi_exp_method_naive uses opt_window_wnaf_exp for exponentiation. |
| multi_exp_method_naive_plain | As multi_exp_method_naive, but uses operator * rather than opt_window_wnaf_exp. |
| multi_exp_method_bos_coster | A variant of the Bos-Coster algorithm [1], with implementation suggestions from [2]. [1] = Bos and Coster, "Addition chain heuristics", CRYPTO '89 [2] = Bernstein, Duif, Lange, Schwabe, and Yang, "High-speed high-security signatures", CHES '11 |
| multi_exp_method_BDLO12 | A special case of Pippenger's algorithm from Page 15 of Bernstein, Doumen, Lange, Oosterwijk, "Faster batch forgery identification", INDOCRYPT 2012 (https://eprint.iacr.org/2012/549.pdf) Requires that T implements .dbl() |
| multi_exp_method_BDLO12_signed | Similar to multi_exp_method_BDLO12, but using signed digits. |
Definition at line 21 of file multiexp.hpp.
Function Documentation
◆ alt_bn128_affine_reduced_pairing()
| alt_bn128_GT libff::alt_bn128_affine_reduced_pairing | ( | const alt_bn128_G1 & | P, |
| const alt_bn128_G2 & | Q | ||
| ) |
◆ alt_bn128_ate_double_miller_loop()
| alt_bn128_Fq12 libff::alt_bn128_ate_double_miller_loop | ( | const alt_bn128_ate_G1_precomp & | prec_P1, |
| const alt_bn128_ate_G2_precomp & | prec_Q1, | ||
| const alt_bn128_ate_G1_precomp & | prec_P2, | ||
| const alt_bn128_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 453 of file alt_bn128_pairing.cpp.

◆ alt_bn128_ate_miller_loop()
| alt_bn128_Fq12 libff::alt_bn128_ate_miller_loop | ( | const alt_bn128_ate_G1_precomp & | prec_P, |
| const alt_bn128_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 401 of file alt_bn128_pairing.cpp.

◆ alt_bn128_ate_pairing()
| alt_bn128_Fq12 libff::alt_bn128_ate_pairing | ( | const alt_bn128_G1 & | P, |
| const alt_bn128_G2 & | Q | ||
| ) |
Definition at line 524 of file alt_bn128_pairing.cpp.

◆ alt_bn128_ate_precompute_G1()
| alt_bn128_ate_G1_precomp libff::alt_bn128_ate_precompute_G1 | ( | const alt_bn128_G1 & | P | ) |
Definition at line 325 of file alt_bn128_pairing.cpp.

◆ alt_bn128_ate_precompute_G2()
| alt_bn128_ate_G2_precomp libff::alt_bn128_ate_precompute_G2 | ( | const alt_bn128_G2 & | Q | ) |
Definition at line 340 of file alt_bn128_pairing.cpp.
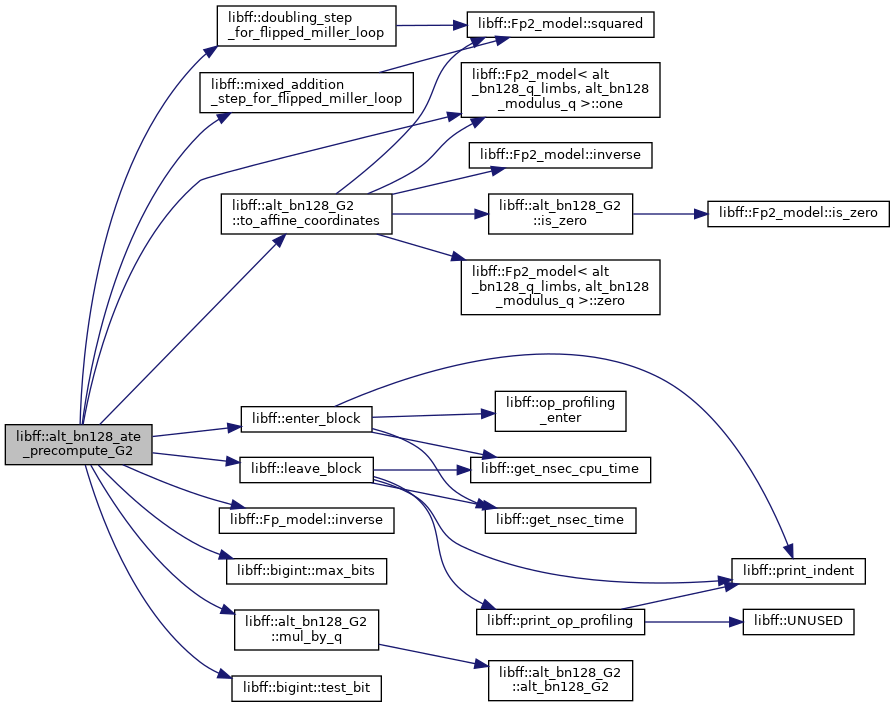

◆ alt_bn128_ate_reduced_pairing()
| alt_bn128_GT libff::alt_bn128_ate_reduced_pairing | ( | const alt_bn128_G1 & | P, |
| const alt_bn128_G2 & | Q | ||
| ) |
Definition at line 535 of file alt_bn128_pairing.cpp.
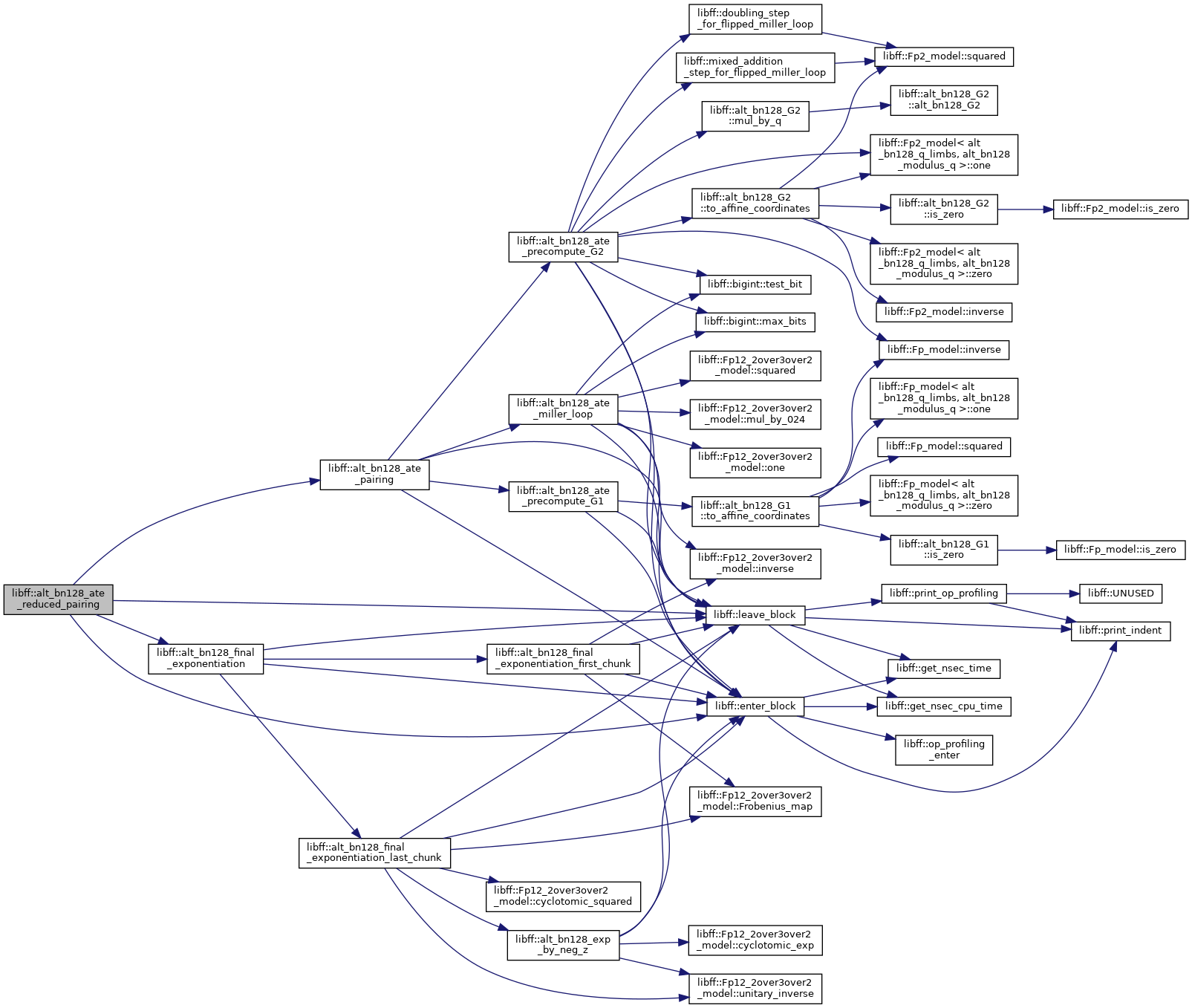

◆ alt_bn128_double_miller_loop()
| alt_bn128_Fq12 libff::alt_bn128_double_miller_loop | ( | const alt_bn128_G1_precomp & | prec_P1, |
| const alt_bn128_G2_precomp & | prec_Q1, | ||
| const alt_bn128_G1_precomp & | prec_P2, | ||
| const alt_bn128_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 563 of file alt_bn128_pairing.cpp.
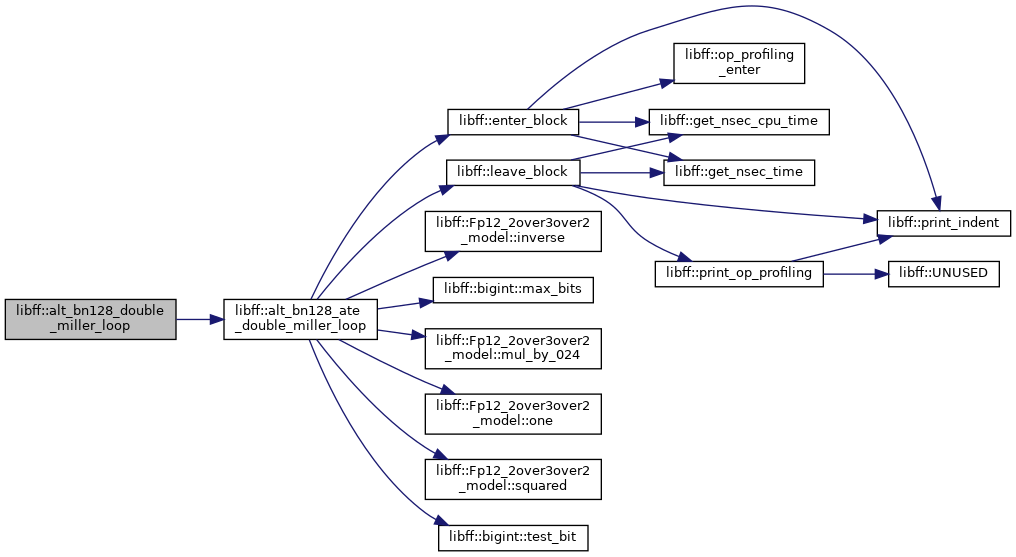

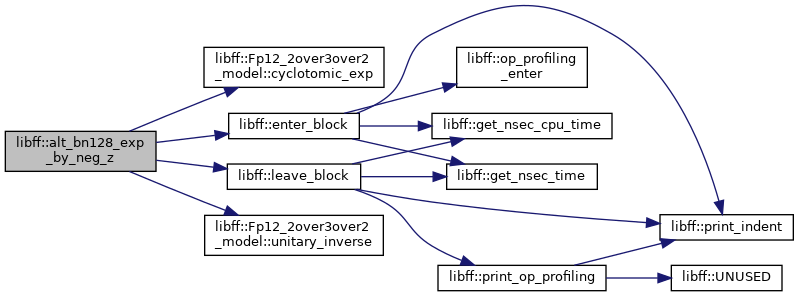
◆ alt_bn128_exp_by_neg_z()
| alt_bn128_Fq12 libff::alt_bn128_exp_by_neg_z | ( | const alt_bn128_Fq12 & | elt | ) |
Definition at line 141 of file alt_bn128_pairing.cpp.

◆ alt_bn128_final_exponentiation()
| alt_bn128_GT libff::alt_bn128_final_exponentiation | ( | const alt_bn128_Fq12 & | elt | ) |
Definition at line 231 of file alt_bn128_pairing.cpp.
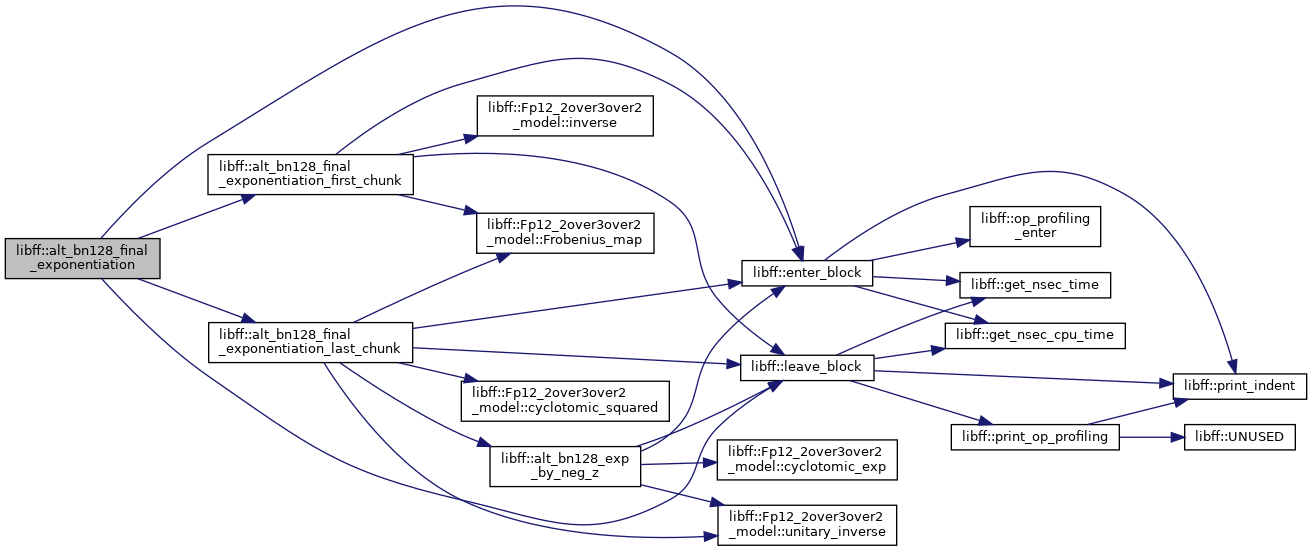

◆ alt_bn128_final_exponentiation_first_chunk()
| alt_bn128_Fq12 libff::alt_bn128_final_exponentiation_first_chunk | ( | const alt_bn128_Fq12 & | elt | ) |
Definition at line 113 of file alt_bn128_pairing.cpp.
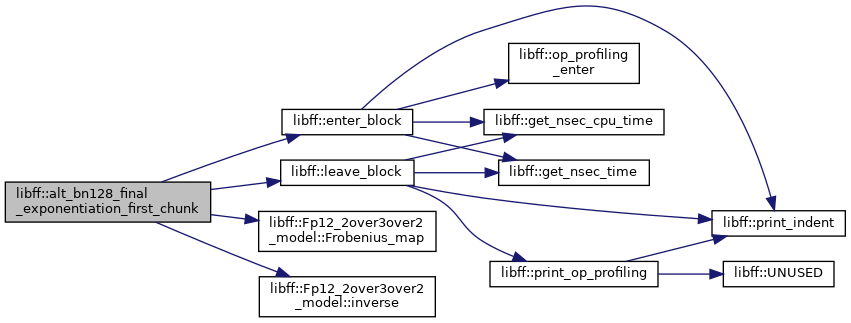

◆ alt_bn128_final_exponentiation_last_chunk()
| alt_bn128_Fq12 libff::alt_bn128_final_exponentiation_last_chunk | ( | const alt_bn128_Fq12 & | elt | ) |
Definition at line 155 of file alt_bn128_pairing.cpp.
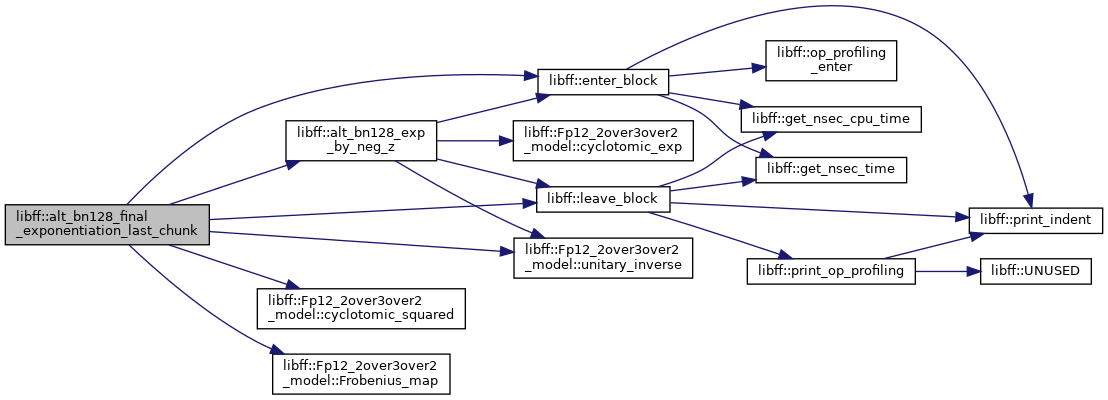

◆ alt_bn128_miller_loop()
| alt_bn128_Fq12 libff::alt_bn128_miller_loop | ( | const alt_bn128_G1_precomp & | prec_P, |
| const alt_bn128_G2_precomp & | prec_Q | ||
| ) |
Definition at line 557 of file alt_bn128_pairing.cpp.
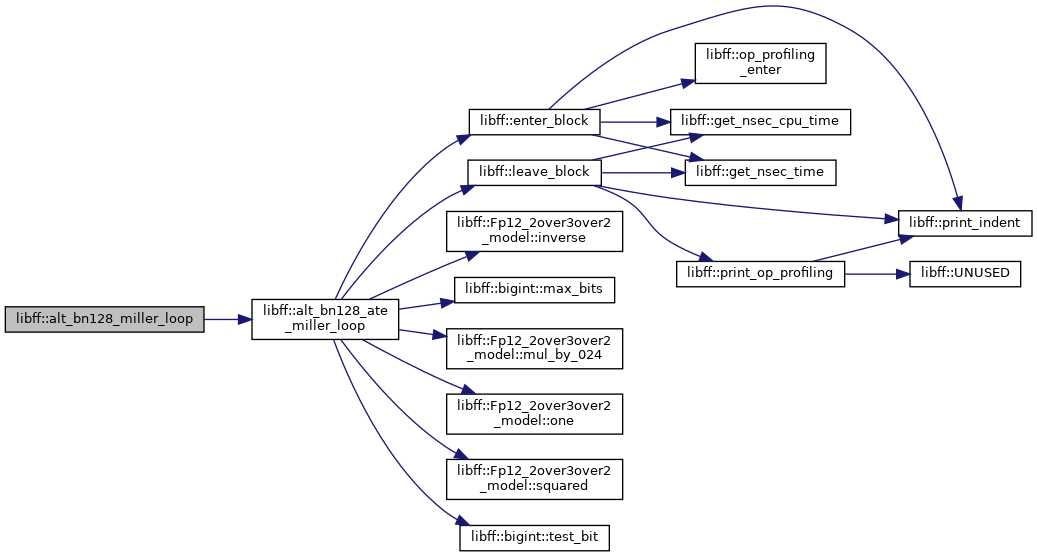

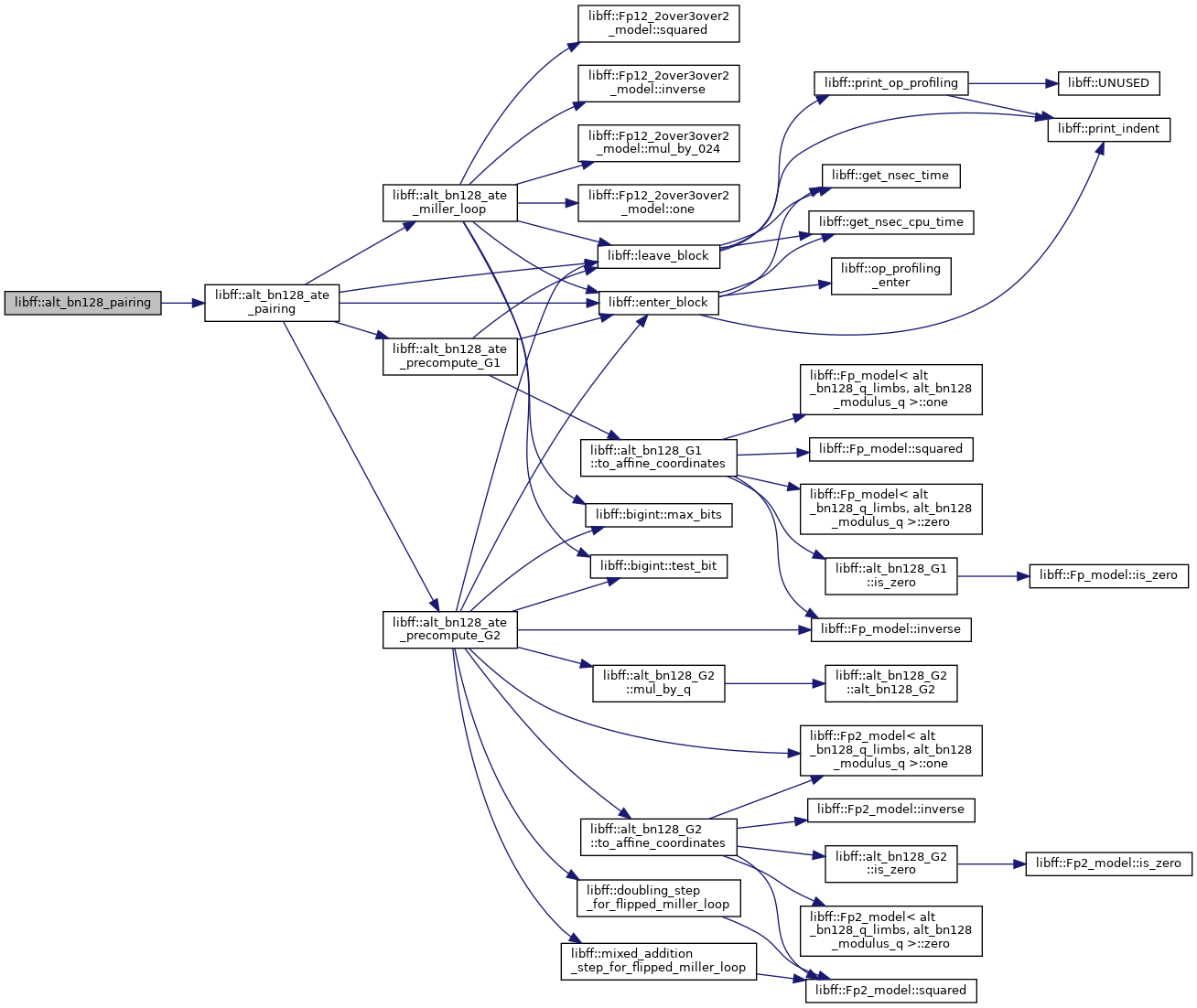
◆ alt_bn128_pairing()
| alt_bn128_Fq12 libff::alt_bn128_pairing | ( | const alt_bn128_G1 & | P, |
| const alt_bn128_G2 & | Q | ||
| ) |
Definition at line 572 of file alt_bn128_pairing.cpp.

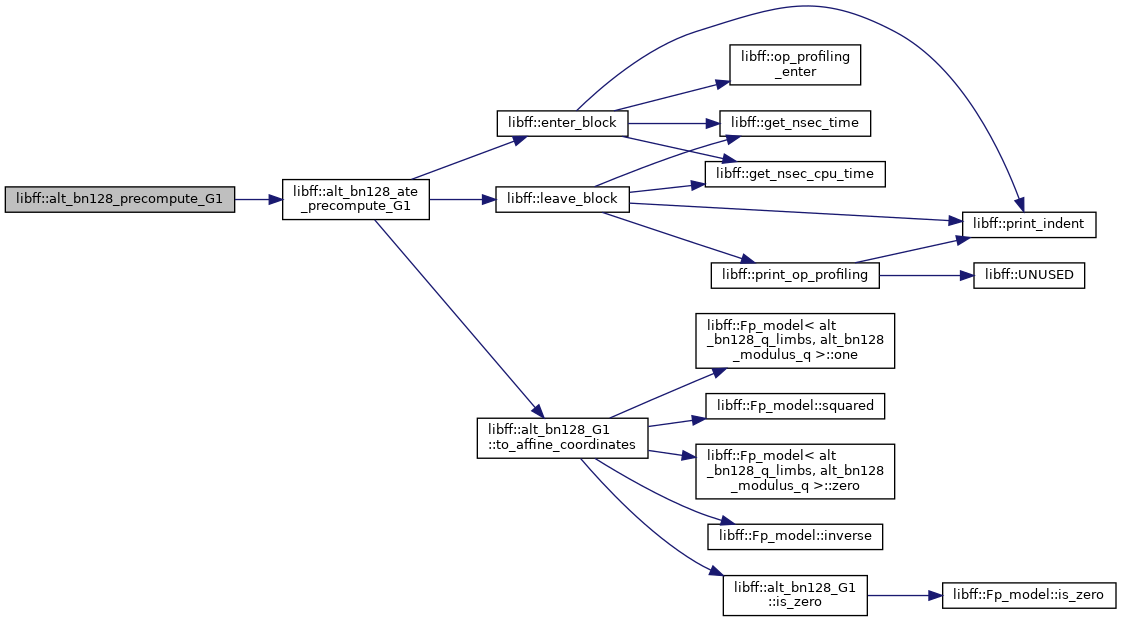
◆ alt_bn128_precompute_G1()
| alt_bn128_G1_precomp libff::alt_bn128_precompute_G1 | ( | const alt_bn128_G1 & | P | ) |
Definition at line 547 of file alt_bn128_pairing.cpp.

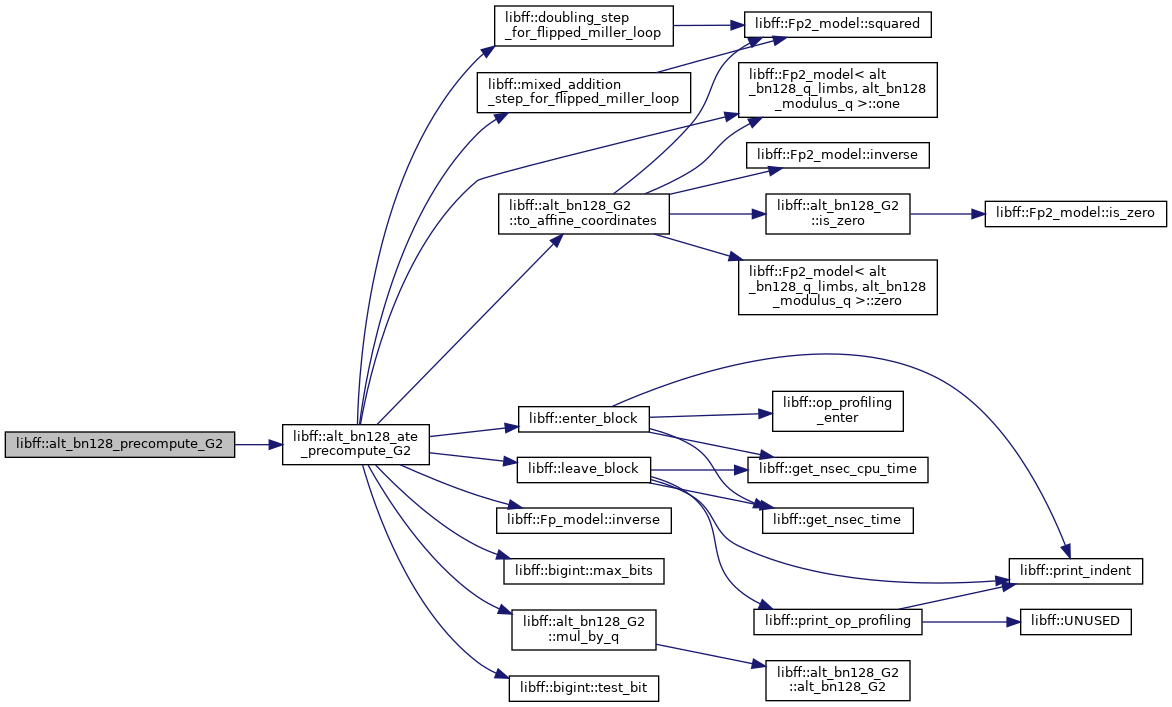
◆ alt_bn128_precompute_G2()
| alt_bn128_G2_precomp libff::alt_bn128_precompute_G2 | ( | const alt_bn128_G2 & | Q | ) |
Definition at line 552 of file alt_bn128_pairing.cpp.

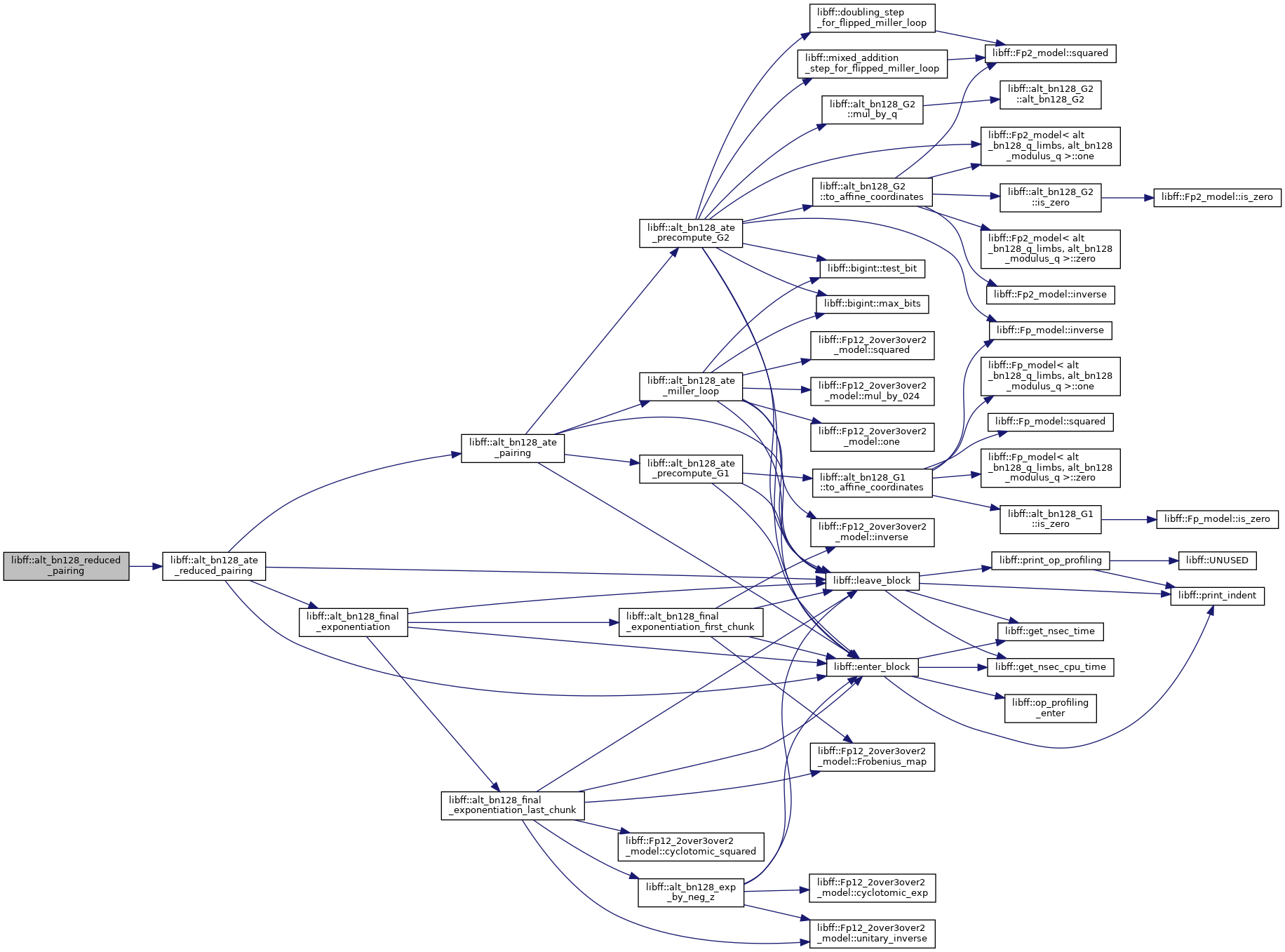
◆ alt_bn128_reduced_pairing()
| alt_bn128_GT libff::alt_bn128_reduced_pairing | ( | const alt_bn128_G1 & | P, |
| const alt_bn128_G2 & | Q | ||
| ) |
Definition at line 577 of file alt_bn128_pairing.cpp.

◆ batch_exp() [1/2]
| std::vector<T> libff::batch_exp | ( | const size_t | scalar_size, |
| const size_t | window, | ||
| const window_table< T > & | table, | ||
| const std::vector< FieldT > & | v | ||
| ) |
◆ batch_exp() [2/2]
| std::vector<T> libff::batch_exp | ( | const size_t | scalar_size, |
| const size_t | window, | ||
| const window_table< T > & | table, | ||
| const std::vector< FieldT > & | v, | ||
| size_t | num_entries | ||
| ) |
◆ batch_exp_with_coeff()
| std::vector<T> libff::batch_exp_with_coeff | ( | const size_t | scalar_size, |
| const size_t | window, | ||
| const window_table< T > & | table, | ||
| const FieldT & | coeff, | ||
| const std::vector< FieldT > & | v | ||
| ) |
◆ batch_invert()
| void libff::batch_invert | ( | std::vector< FieldT > & | vec | ) |
◆ batch_to_special()
| void libff::batch_to_special | ( | std::vector< T > & | vec | ) |
◆ bigint_from_hex()
| void libff::bigint_from_hex | ( | BigIntT & | v, |
| const std::string & | hex | ||
| ) |
◆ bigint_to_hex()
| std::string libff::bigint_to_hex | ( | const BigIntT & | v, |
| bool | prefix = false |
||
| ) |
◆ bitreverse()
| size_t libff::bitreverse | ( | size_t | n, |
| const size_t | l | ||
| ) |
◆ bls12_377_affine_reduced_pairing()
| bls12_377_GT libff::bls12_377_affine_reduced_pairing | ( | const bls12_377_G1 & | P, |
| const bls12_377_G2 & | Q | ||
| ) |
◆ bls12_377_ate_double_miller_loop()
| bls12_377_Fq12 libff::bls12_377_ate_double_miller_loop | ( | const bls12_377_ate_G1_precomp & | prec_P1, |
| const bls12_377_ate_G2_precomp & | prec_Q1, | ||
| const bls12_377_ate_G1_precomp & | prec_P2, | ||
| const bls12_377_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 465 of file bls12_377_pairing.cpp.
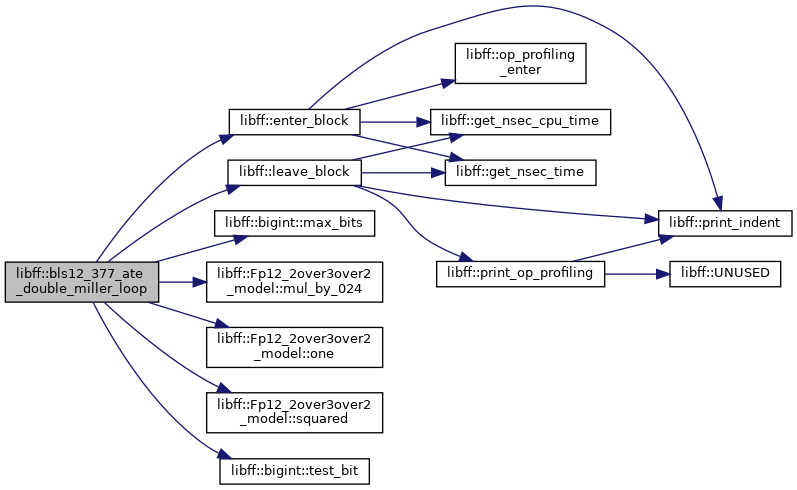

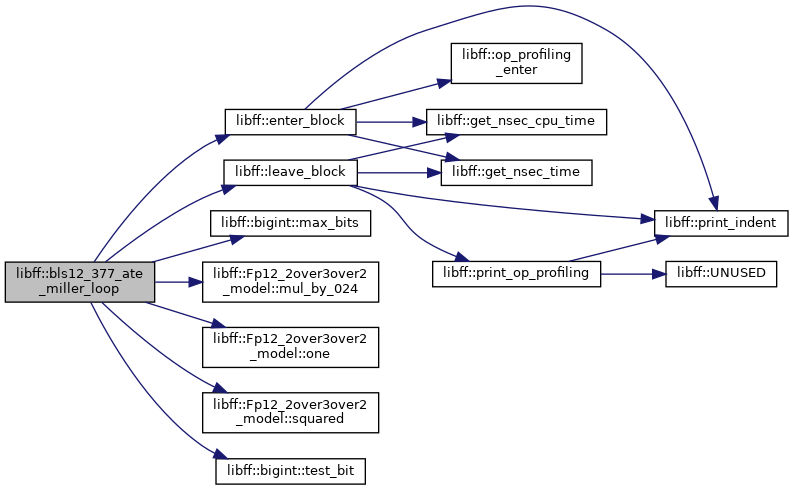
◆ bls12_377_ate_miller_loop()
| bls12_377_Fq12 libff::bls12_377_ate_miller_loop | ( | const bls12_377_ate_G1_precomp & | prec_P, |
| const bls12_377_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 408 of file bls12_377_pairing.cpp.

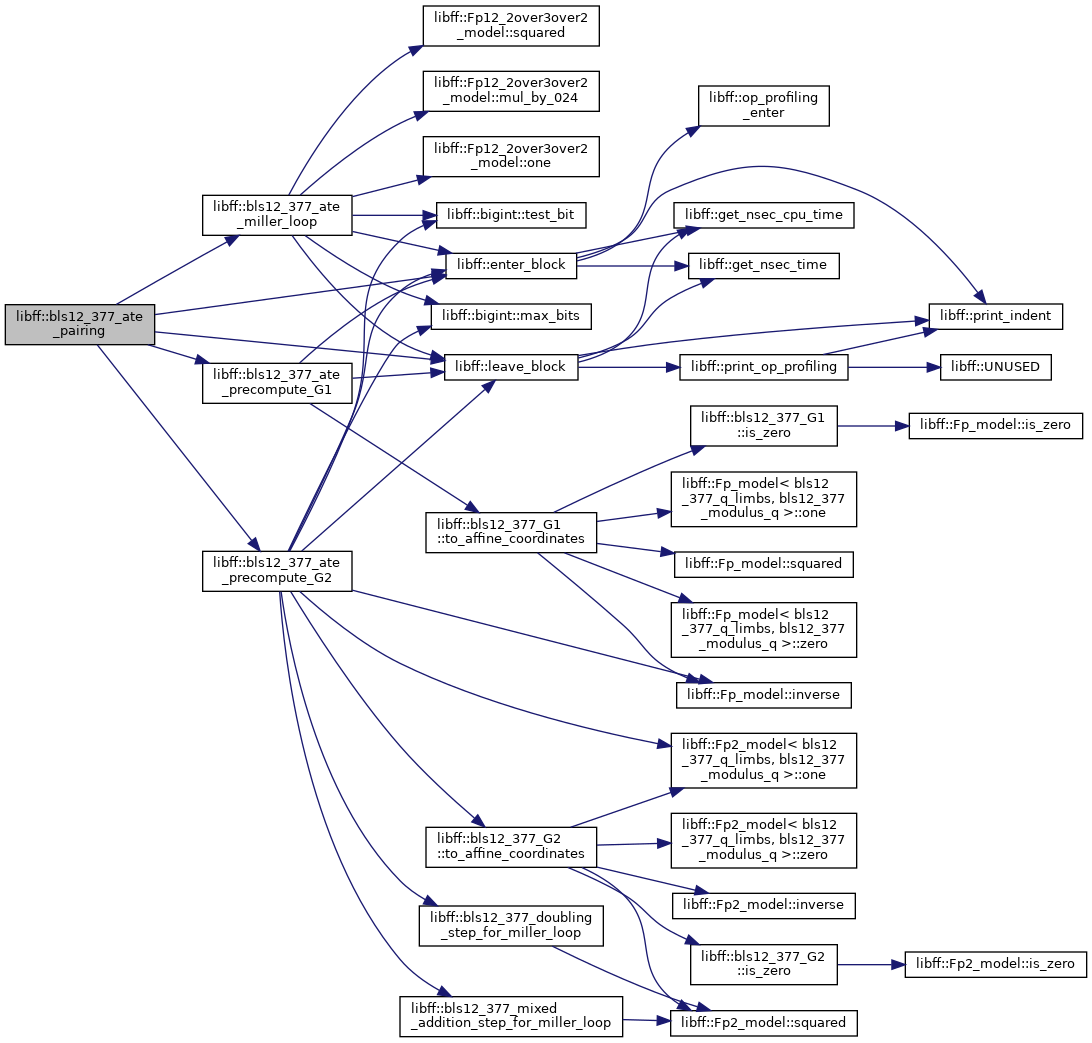
◆ bls12_377_ate_pairing()
| bls12_377_Fq12 libff::bls12_377_ate_pairing | ( | const bls12_377_G1 & | P, |
| const bls12_377_G2 & | Q | ||
| ) |
Definition at line 519 of file bls12_377_pairing.cpp.

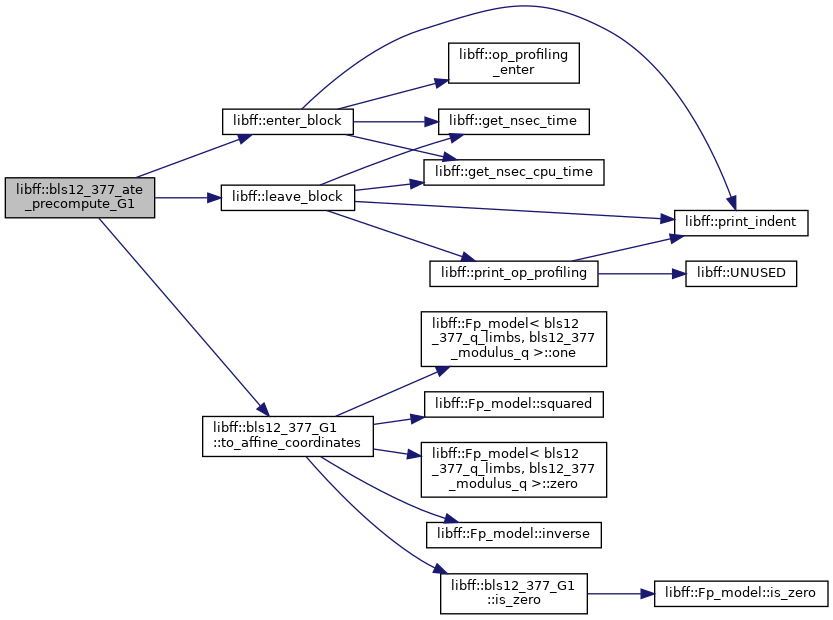
◆ bls12_377_ate_precompute_G1()
| bls12_377_ate_G1_precomp libff::bls12_377_ate_precompute_G1 | ( | const bls12_377_G1 & | P | ) |
Definition at line 333 of file bls12_377_pairing.cpp.

◆ bls12_377_ate_precompute_G2()
| bls12_377_ate_G2_precomp libff::bls12_377_ate_precompute_G2 | ( | const bls12_377_G2 & | Q | ) |
Definition at line 363 of file bls12_377_pairing.cpp.
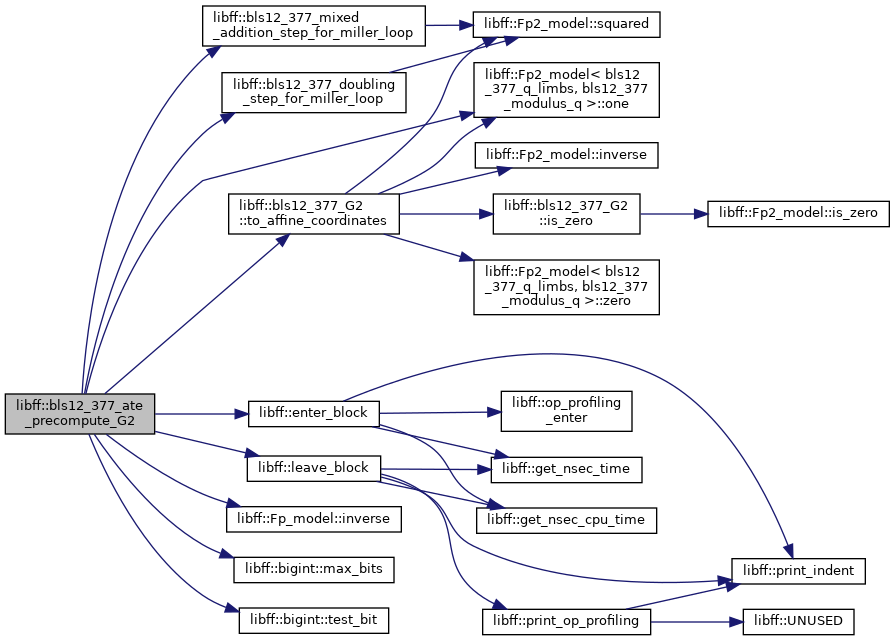

◆ bls12_377_ate_reduced_pairing()
| bls12_377_GT libff::bls12_377_ate_reduced_pairing | ( | const bls12_377_G1 & | P, |
| const bls12_377_G2 & | Q | ||
| ) |
Definition at line 530 of file bls12_377_pairing.cpp.
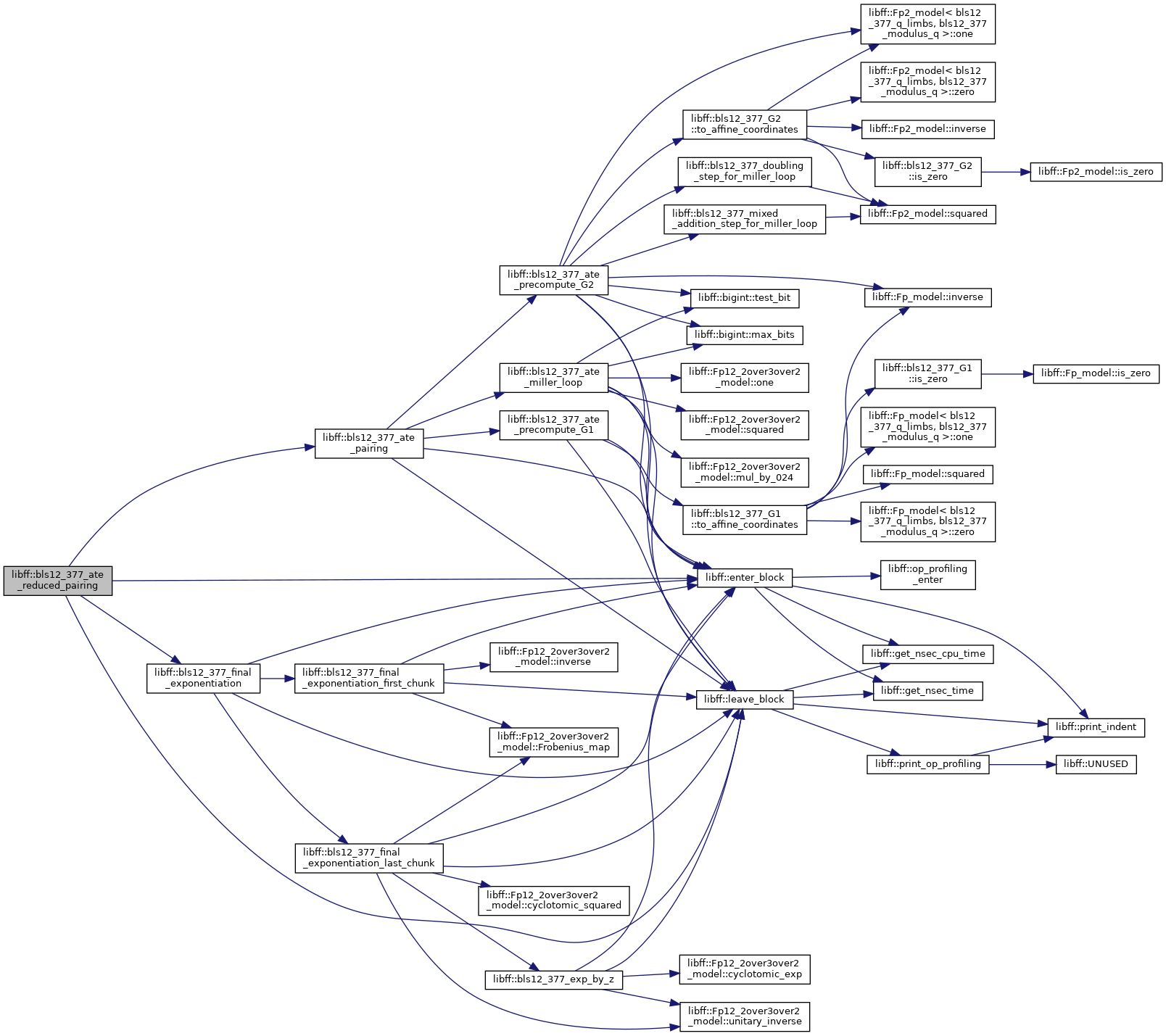

◆ bls12_377_double_miller_loop()
| bls12_377_Fq12 libff::bls12_377_double_miller_loop | ( | const bls12_377_G1_precomp & | prec_P1, |
| const bls12_377_G2_precomp & | prec_Q1, | ||
| const bls12_377_G1_precomp & | prec_P2, | ||
| const bls12_377_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 558 of file bls12_377_pairing.cpp.
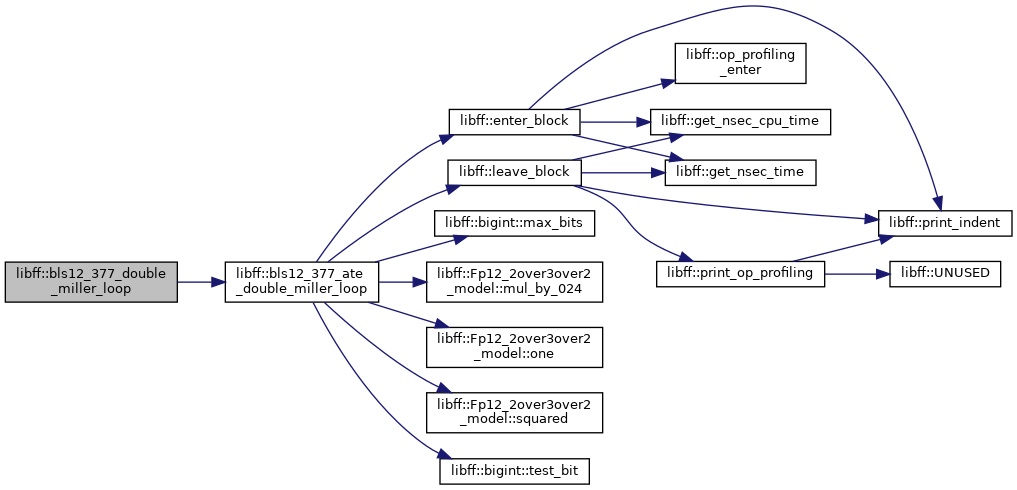

◆ bls12_377_doubling_step_for_miller_loop()
| void libff::bls12_377_doubling_step_for_miller_loop | ( | const bls12_377_Fq | two_inv, |
| bls12_377_G2 & | current, | ||
| bls12_377_ate_ell_coeffs & | c | ||
| ) |
Definition at line 239 of file bls12_377_pairing.cpp.


◆ bls12_377_exp_by_z()
| bls12_377_Fq12 libff::bls12_377_exp_by_z | ( | const bls12_377_Fq12 & | elt | ) |
Definition at line 137 of file bls12_377_pairing.cpp.
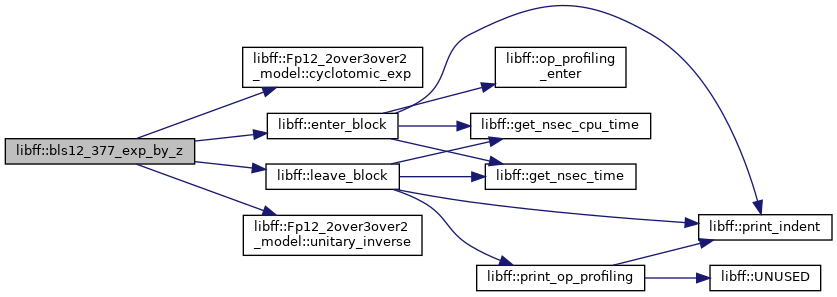

◆ bls12_377_final_exponentiation()
| bls12_377_GT libff::bls12_377_final_exponentiation | ( | const bls12_377_Fq12 & | elt | ) |
Definition at line 217 of file bls12_377_pairing.cpp.
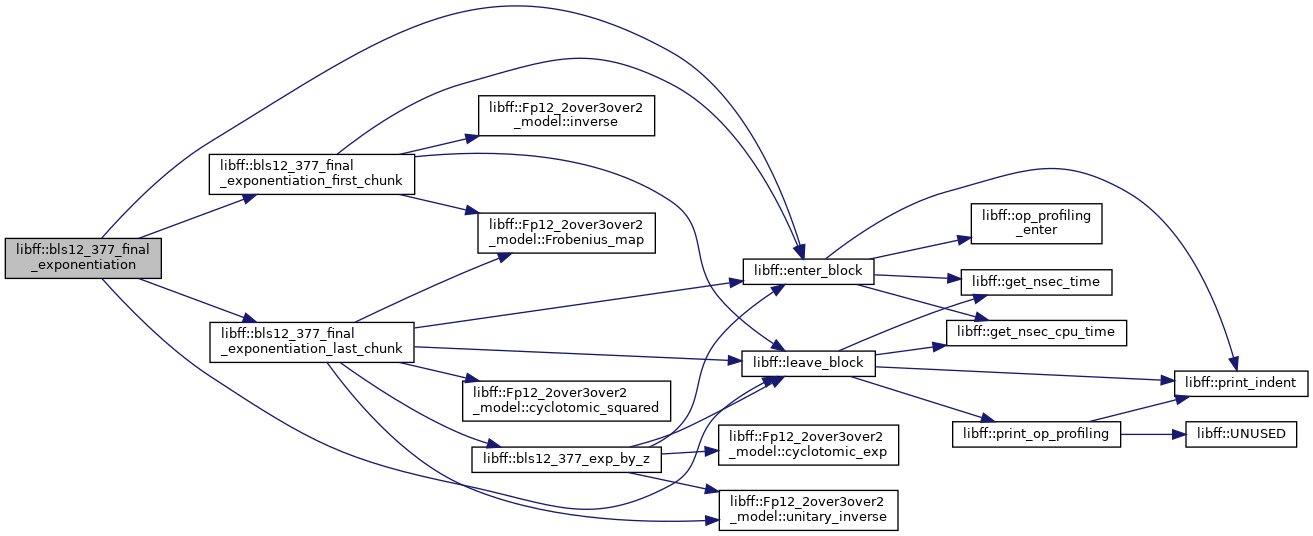

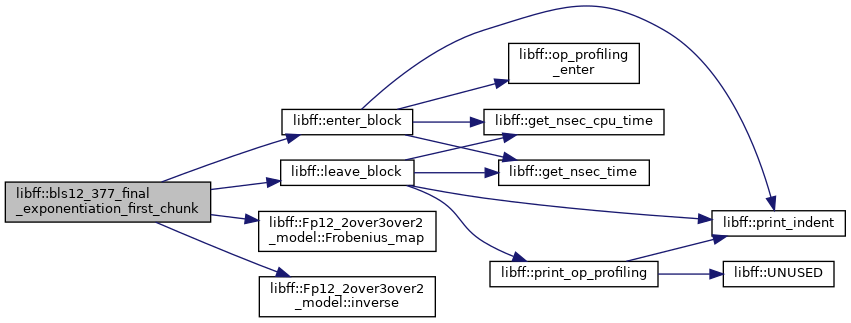
◆ bls12_377_final_exponentiation_first_chunk()
| bls12_377_Fq12 libff::bls12_377_final_exponentiation_first_chunk | ( | const bls12_377_Fq12 & | elt | ) |
Definition at line 109 of file bls12_377_pairing.cpp.

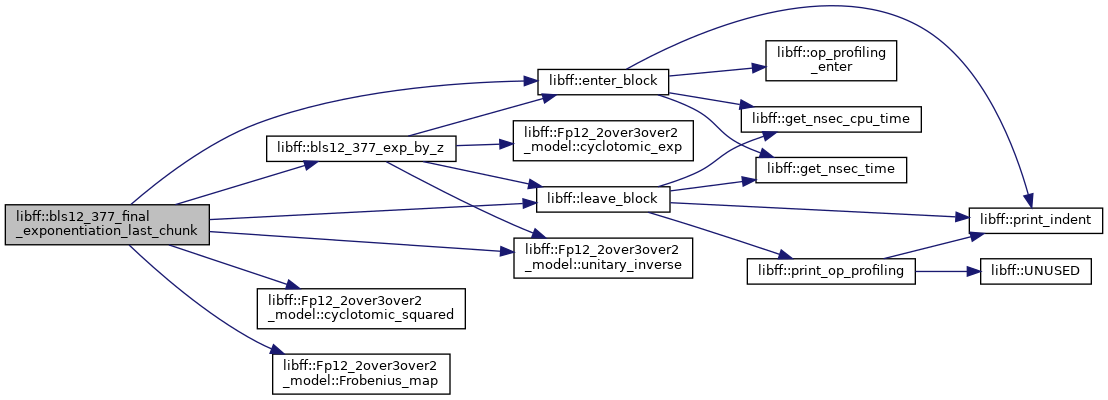
◆ bls12_377_final_exponentiation_last_chunk()
| bls12_377_Fq12 libff::bls12_377_final_exponentiation_last_chunk | ( | const bls12_377_Fq12 & | elt | ) |
Definition at line 151 of file bls12_377_pairing.cpp.

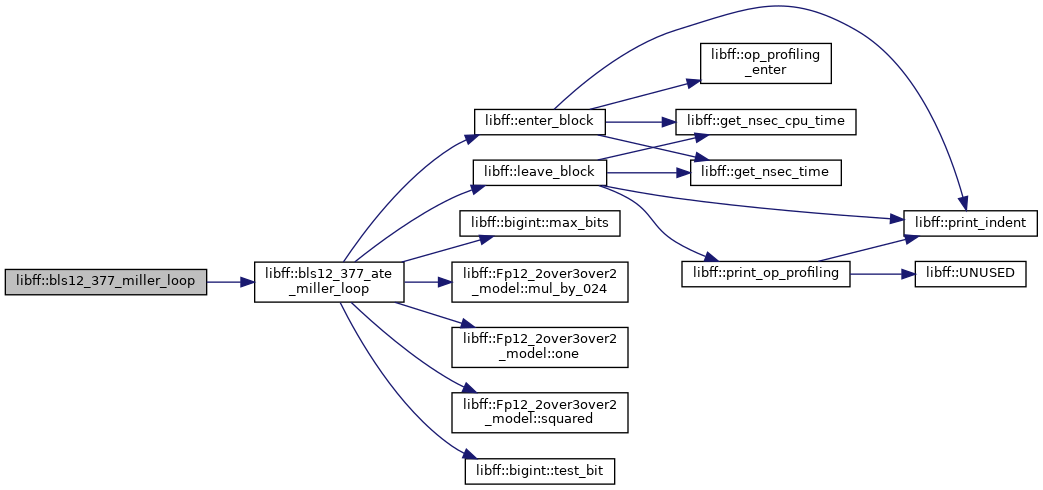
◆ bls12_377_miller_loop()
| bls12_377_Fq12 libff::bls12_377_miller_loop | ( | const bls12_377_G1_precomp & | prec_P, |
| const bls12_377_G2_precomp & | prec_Q | ||
| ) |
Definition at line 552 of file bls12_377_pairing.cpp.

◆ bls12_377_mixed_addition_step_for_miller_loop()
| void libff::bls12_377_mixed_addition_step_for_miller_loop | ( | const bls12_377_G2 & | base, |
| bls12_377_G2 & | current, | ||
| bls12_377_ate_ell_coeffs & | c | ||
| ) |
Definition at line 301 of file bls12_377_pairing.cpp.


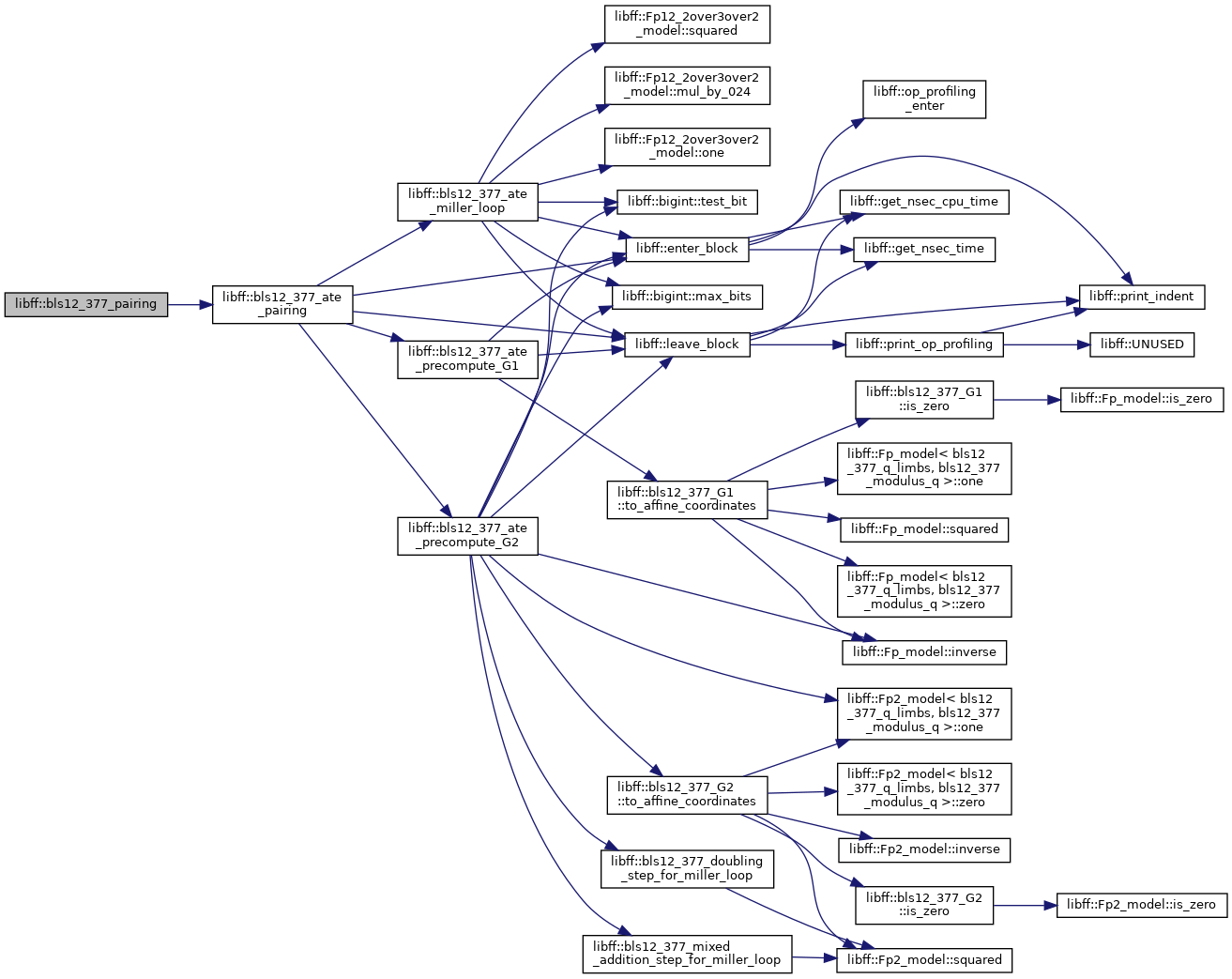
◆ bls12_377_pairing()
| bls12_377_Fq12 libff::bls12_377_pairing | ( | const bls12_377_G1 & | P, |
| const bls12_377_G2 & | Q | ||
| ) |
Definition at line 567 of file bls12_377_pairing.cpp.

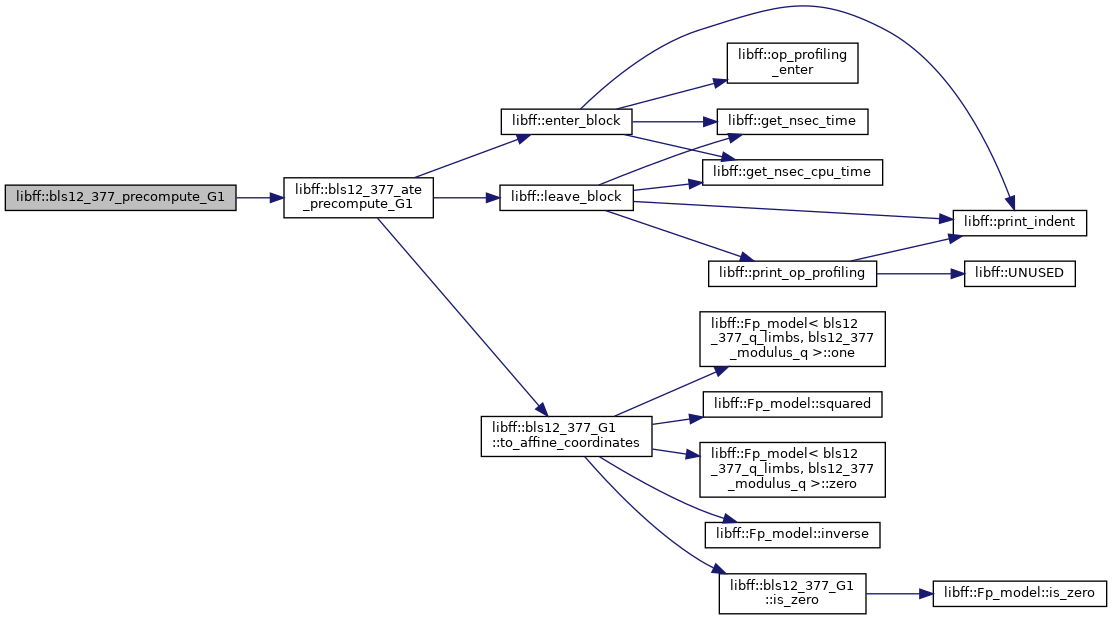
◆ bls12_377_precompute_G1()
| bls12_377_G1_precomp libff::bls12_377_precompute_G1 | ( | const bls12_377_G1 & | P | ) |
Definition at line 542 of file bls12_377_pairing.cpp.

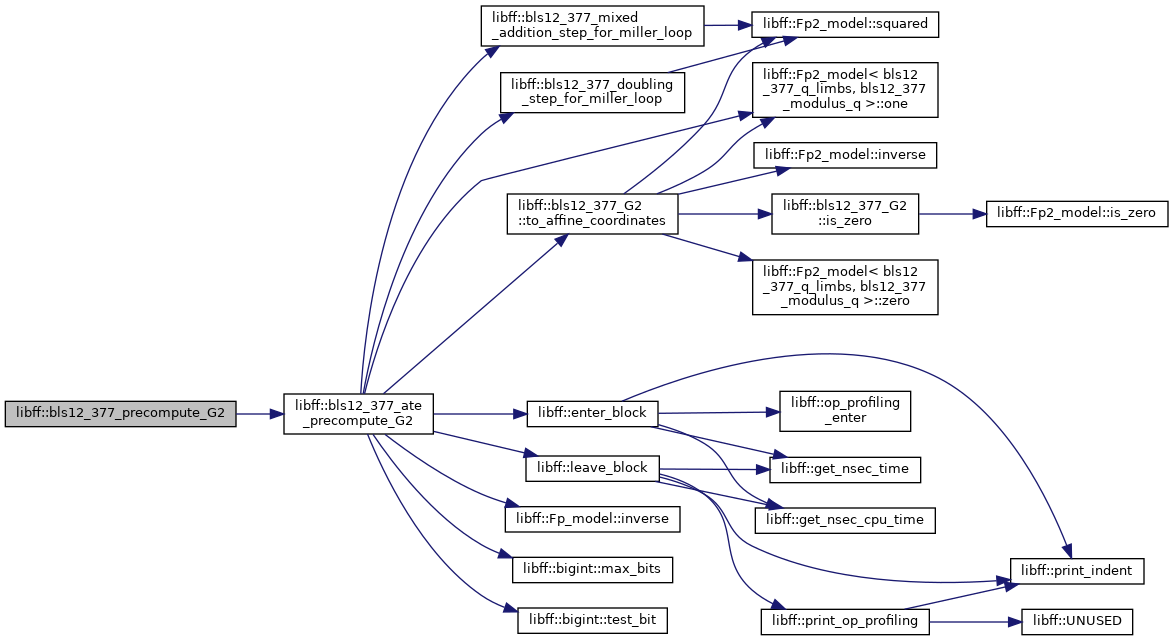
◆ bls12_377_precompute_G2()
| bls12_377_G2_precomp libff::bls12_377_precompute_G2 | ( | const bls12_377_G2 & | Q | ) |
Definition at line 547 of file bls12_377_pairing.cpp.

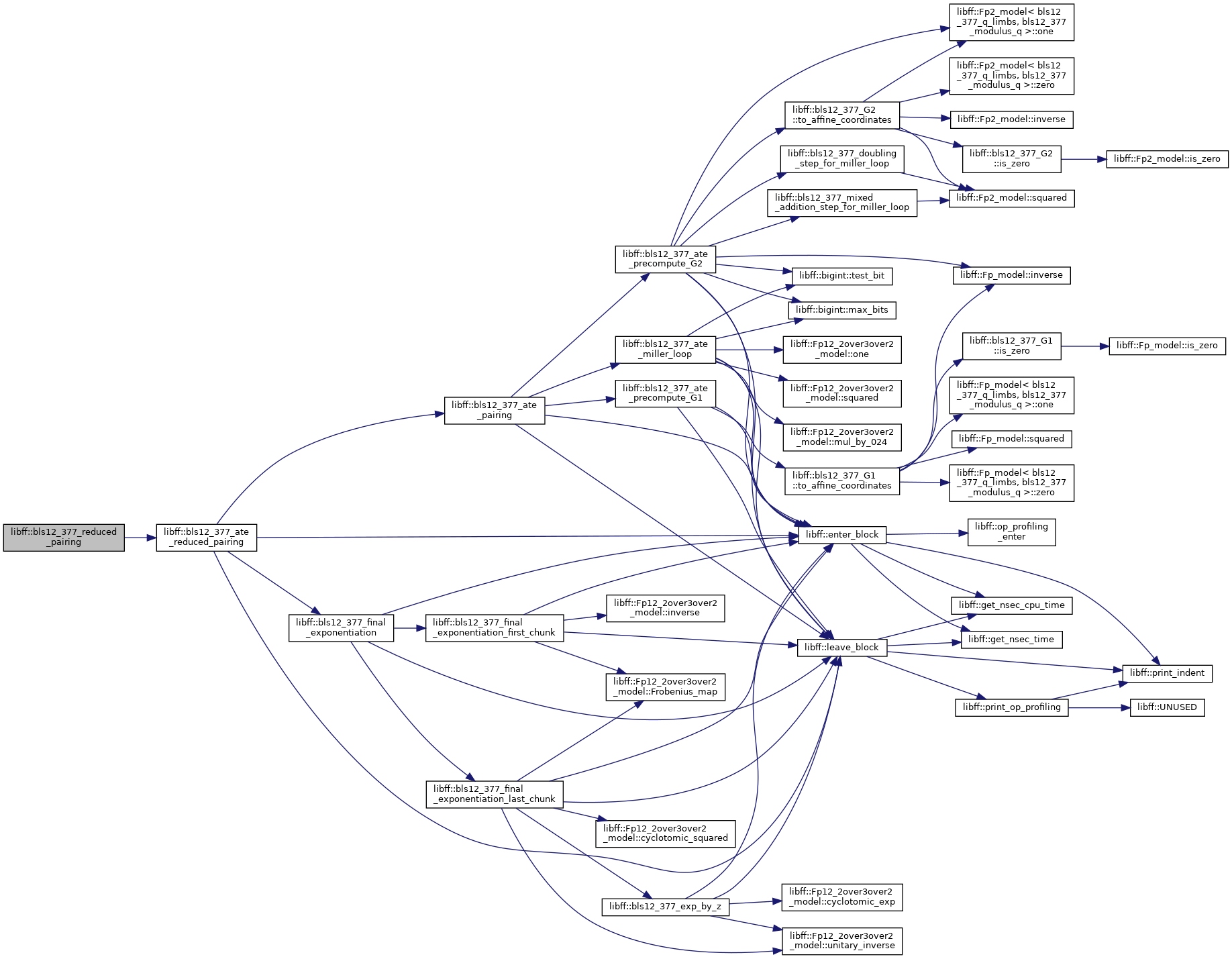
◆ bls12_377_reduced_pairing()
| bls12_377_GT libff::bls12_377_reduced_pairing | ( | const bls12_377_G1 & | P, |
| const bls12_377_G2 & | Q | ||
| ) |
Definition at line 572 of file bls12_377_pairing.cpp.

◆ bls12_381_affine_reduced_pairing()
| bls12_381_GT libff::bls12_381_affine_reduced_pairing | ( | const bls12_381_G1 & | P, |
| const bls12_381_G2 & | Q | ||
| ) |
◆ bls12_381_ate_double_miller_loop()
| bls12_381_Fq12 libff::bls12_381_ate_double_miller_loop | ( | const bls12_381_ate_G1_precomp & | prec_P1, |
| const bls12_381_ate_G2_precomp & | prec_Q1, | ||
| const bls12_381_ate_G1_precomp & | prec_P2, | ||
| const bls12_381_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 415 of file bls12_381_pairing.cpp.
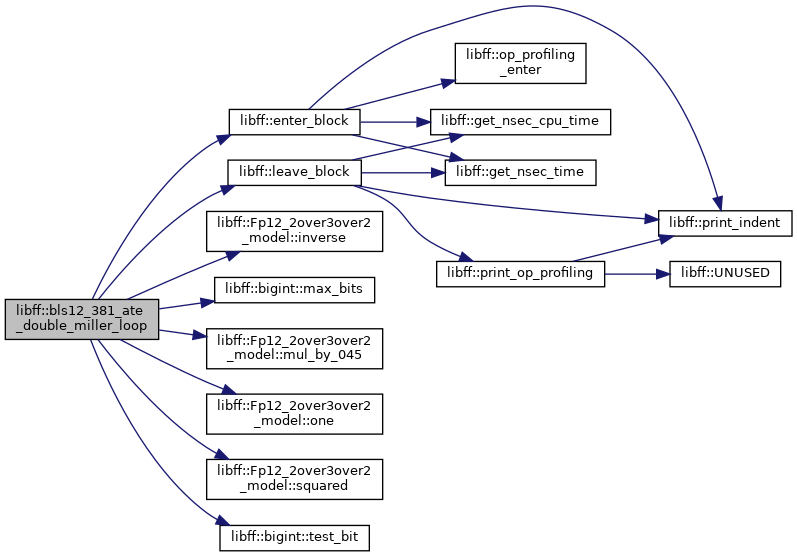

◆ bls12_381_ate_miller_loop()
| bls12_381_Fq12 libff::bls12_381_ate_miller_loop | ( | const bls12_381_ate_G1_precomp & | prec_P, |
| const bls12_381_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 369 of file bls12_381_pairing.cpp.
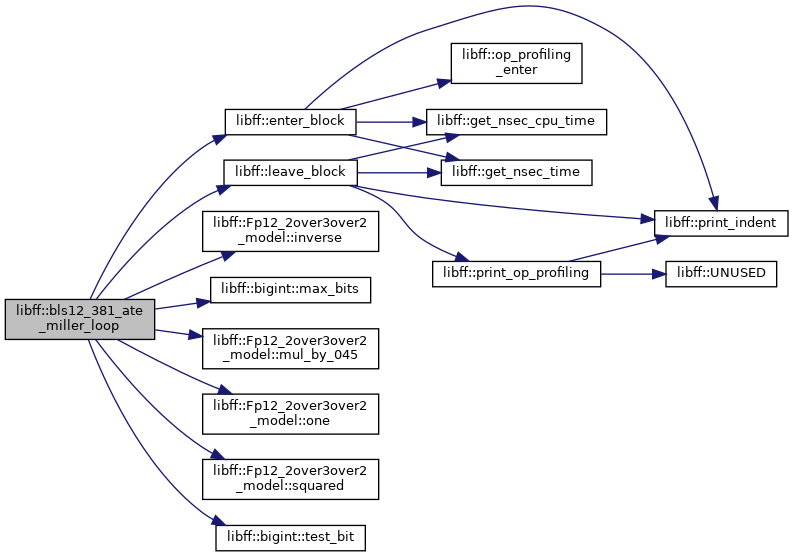

◆ bls12_381_ate_pairing()
| bls12_381_Fq12 libff::bls12_381_ate_pairing | ( | const bls12_381_G1 & | P, |
| const bls12_381_G2 & | Q | ||
| ) |
Definition at line 474 of file bls12_381_pairing.cpp.
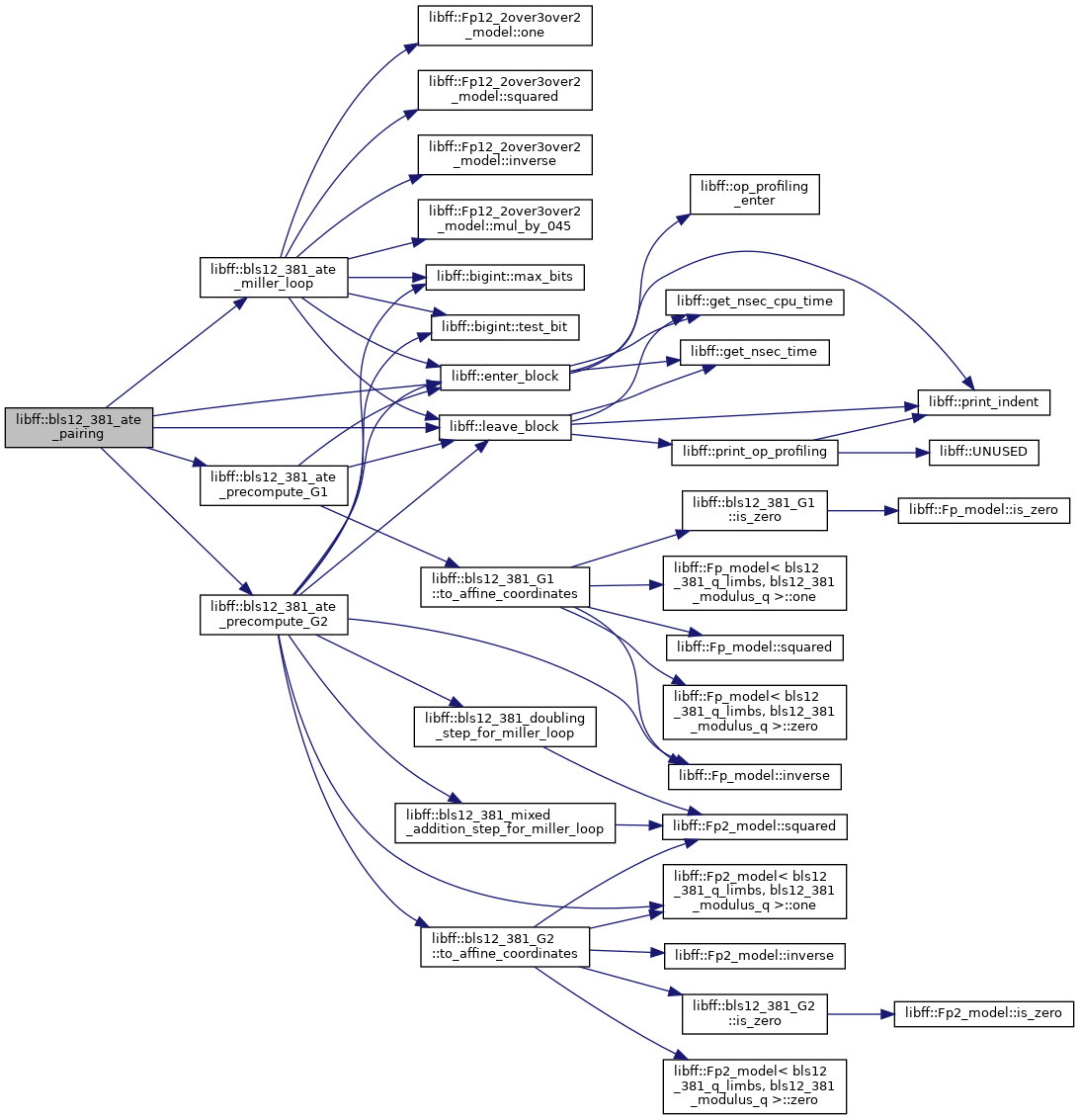

◆ bls12_381_ate_precompute_G1()
| bls12_381_ate_G1_precomp libff::bls12_381_ate_precompute_G1 | ( | const bls12_381_G1 & | P | ) |
Definition at line 309 of file bls12_381_pairing.cpp.
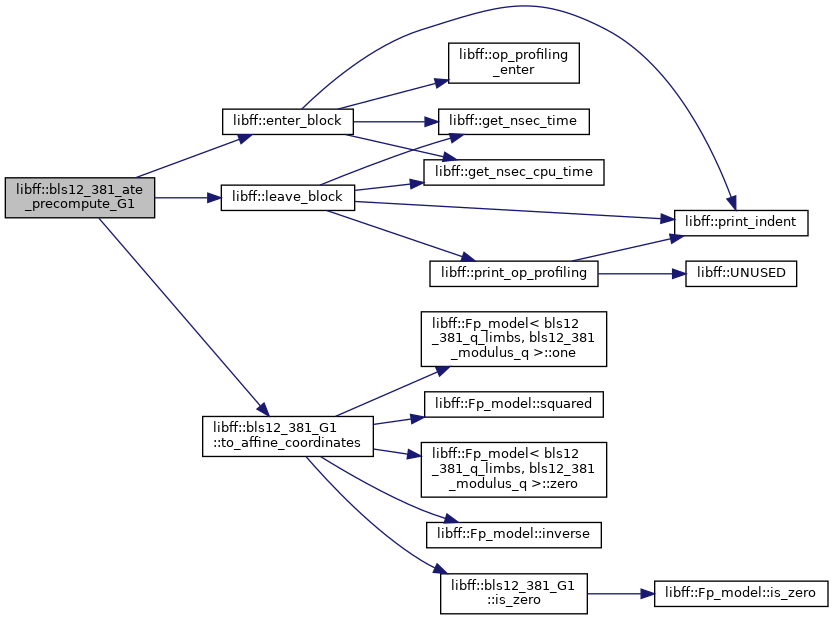

◆ bls12_381_ate_precompute_G2()
| bls12_381_ate_G2_precomp libff::bls12_381_ate_precompute_G2 | ( | const bls12_381_G2 & | Q | ) |
Definition at line 324 of file bls12_381_pairing.cpp.
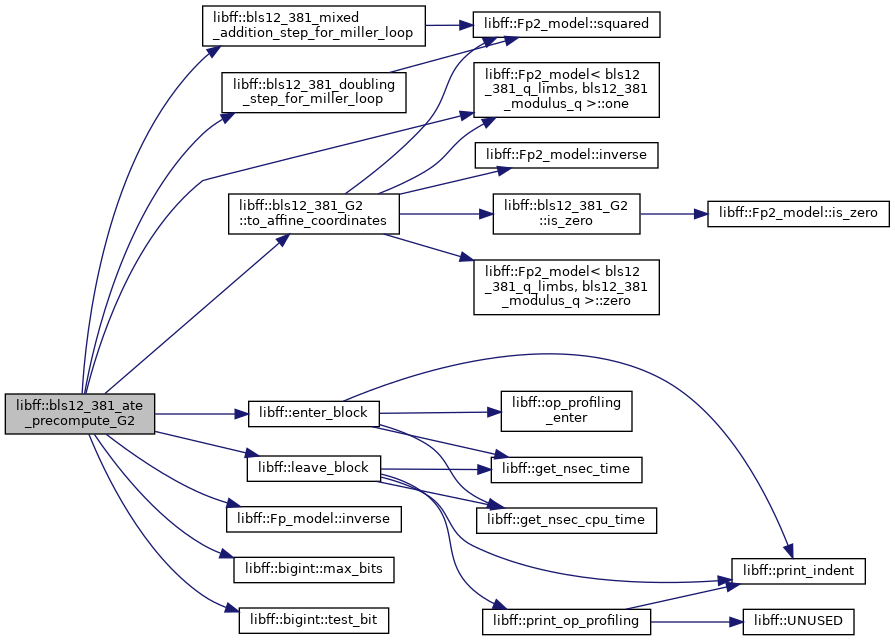

◆ bls12_381_ate_reduced_pairing()
| bls12_381_GT libff::bls12_381_ate_reduced_pairing | ( | const bls12_381_G1 & | P, |
| const bls12_381_G2 & | Q | ||
| ) |
Definition at line 485 of file bls12_381_pairing.cpp.
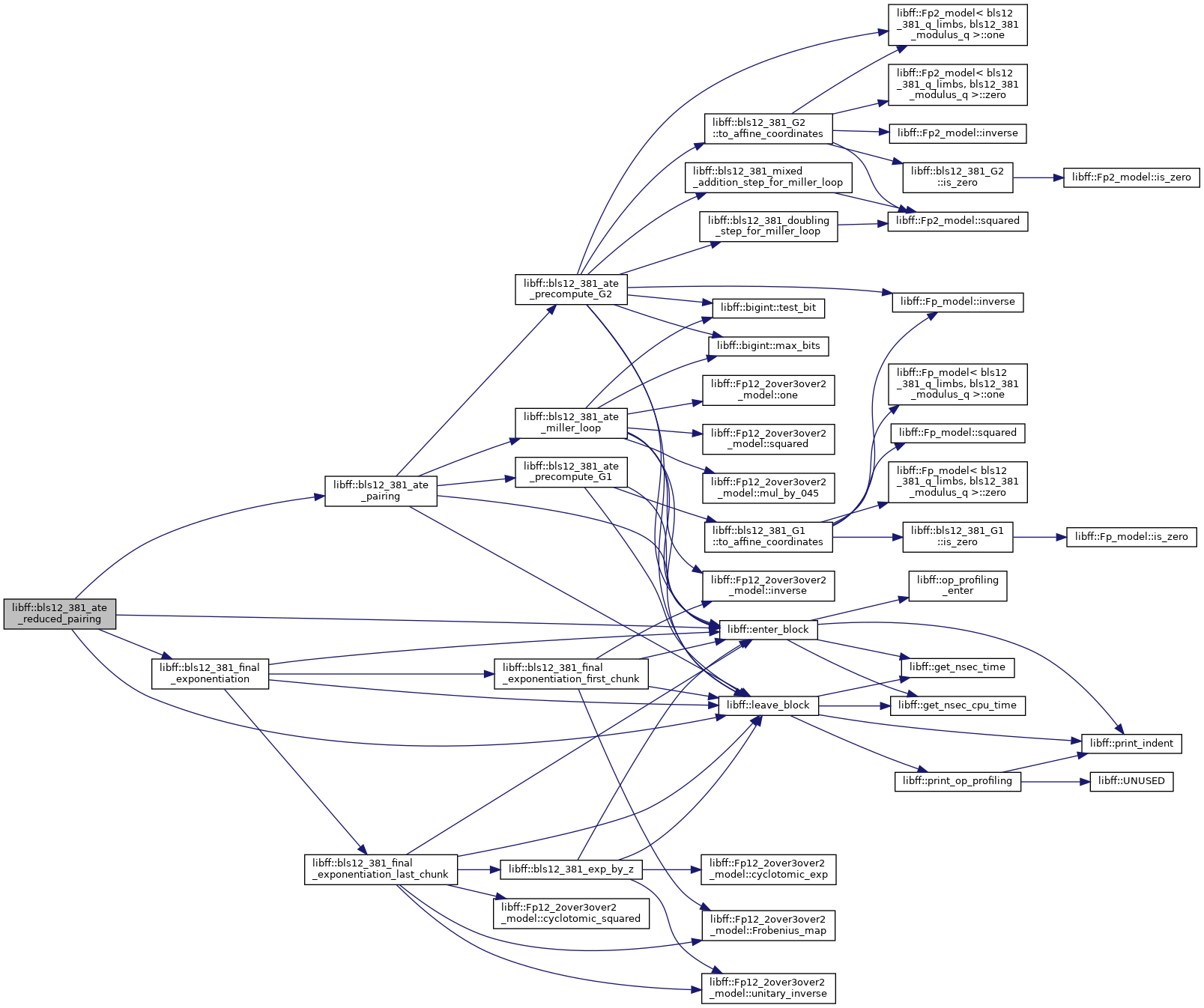

◆ bls12_381_double_miller_loop()
| bls12_381_Fq12 libff::bls12_381_double_miller_loop | ( | const bls12_381_G1_precomp & | prec_P1, |
| const bls12_381_G2_precomp & | prec_Q1, | ||
| const bls12_381_G1_precomp & | prec_P2, | ||
| const bls12_381_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 513 of file bls12_381_pairing.cpp.
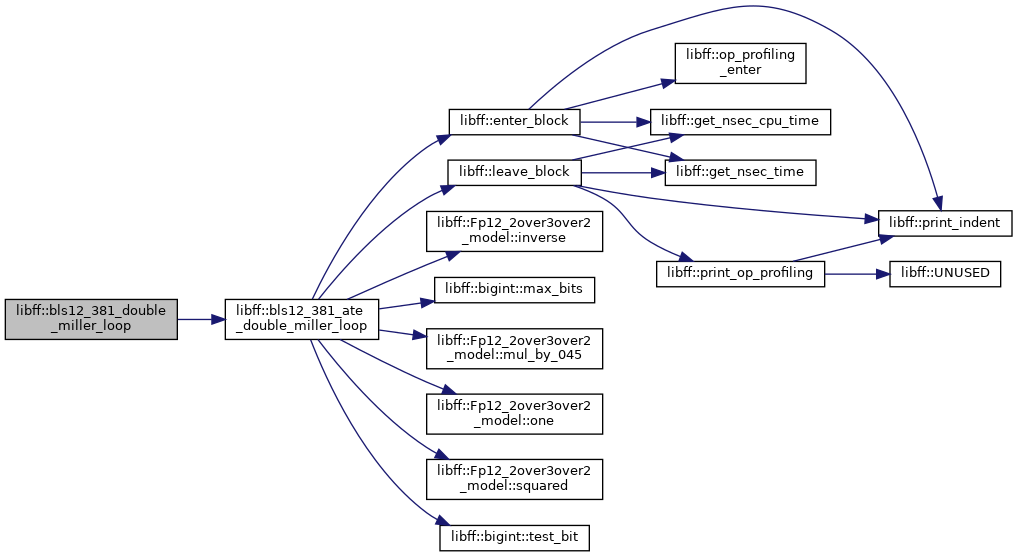

◆ bls12_381_doubling_step_for_miller_loop()
| void libff::bls12_381_doubling_step_for_miller_loop | ( | const bls12_381_Fq | two_inv, |
| bls12_381_G2 & | current, | ||
| bls12_381_ate_ell_coeffs & | c | ||
| ) |
Definition at line 230 of file bls12_381_pairing.cpp.


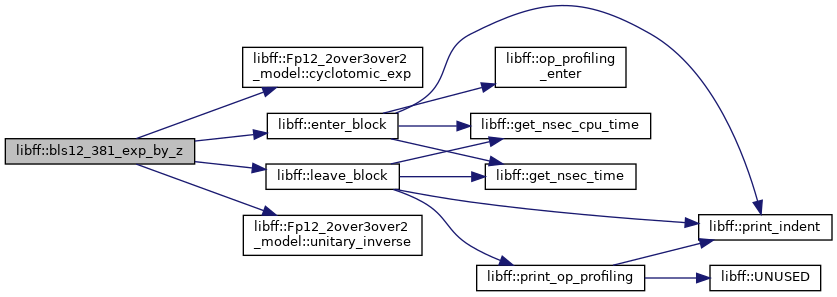
◆ bls12_381_exp_by_z()
| bls12_381_Fq12 libff::bls12_381_exp_by_z | ( | const bls12_381_Fq12 & | elt | ) |
Definition at line 142 of file bls12_381_pairing.cpp.

◆ bls12_381_final_exponentiation()
| bls12_381_GT libff::bls12_381_final_exponentiation | ( | const bls12_381_Fq12 & | elt | ) |
Definition at line 215 of file bls12_381_pairing.cpp.
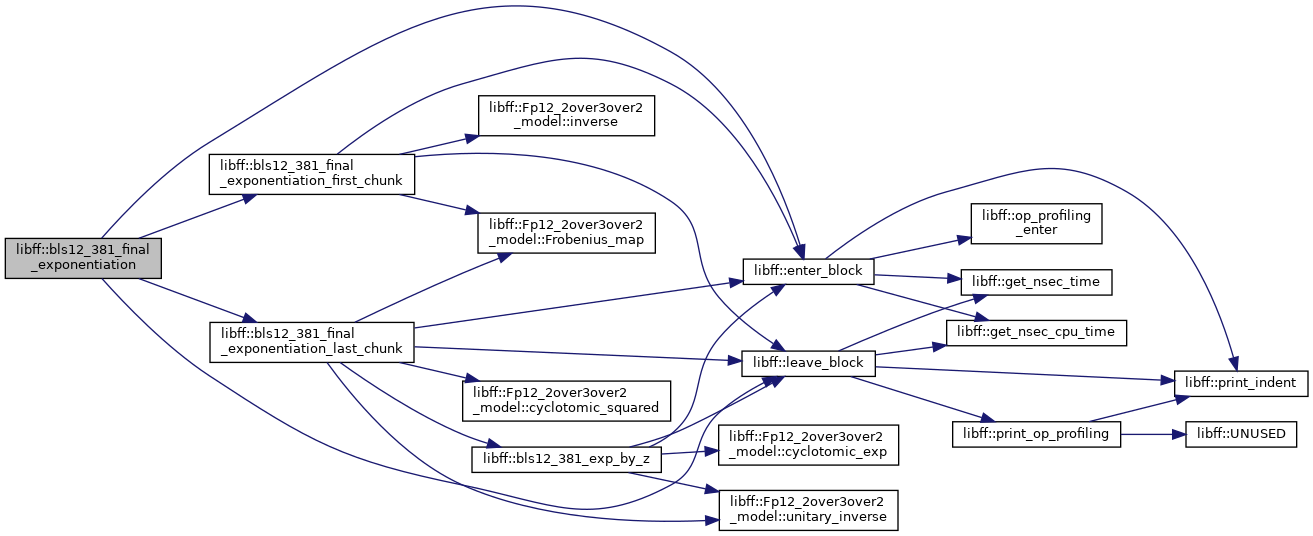

◆ bls12_381_final_exponentiation_first_chunk()
| bls12_381_Fq12 libff::bls12_381_final_exponentiation_first_chunk | ( | const bls12_381_Fq12 & | elt | ) |
Definition at line 114 of file bls12_381_pairing.cpp.
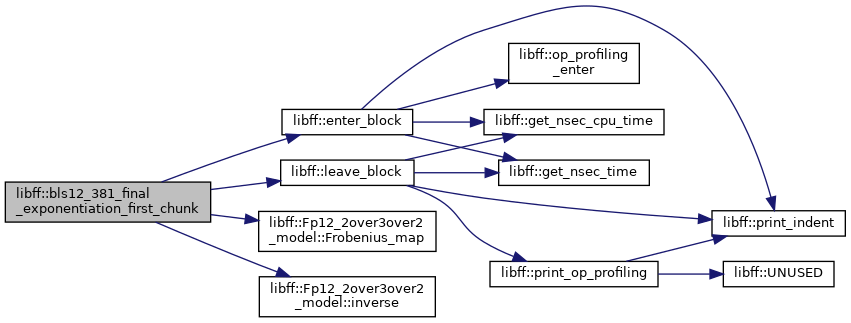

◆ bls12_381_final_exponentiation_last_chunk()
| bls12_381_Fq12 libff::bls12_381_final_exponentiation_last_chunk | ( | const bls12_381_Fq12 & | elt | ) |
Definition at line 156 of file bls12_381_pairing.cpp.
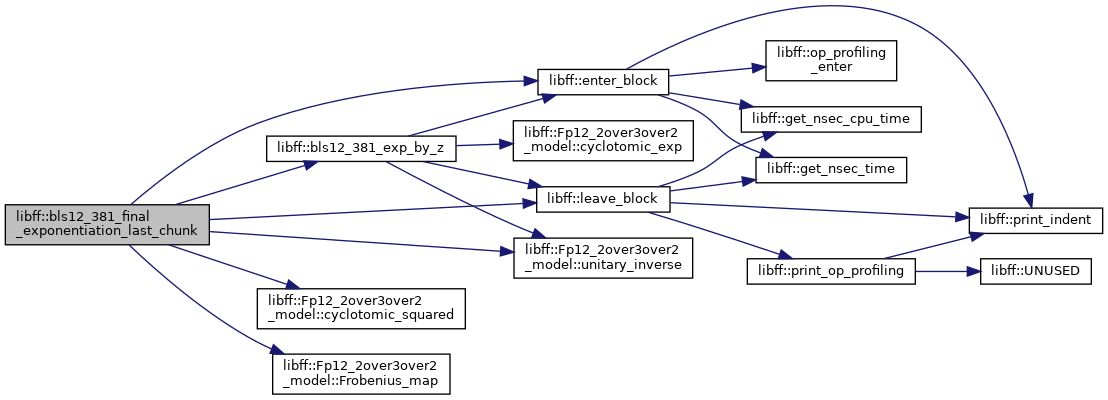

◆ bls12_381_miller_loop()
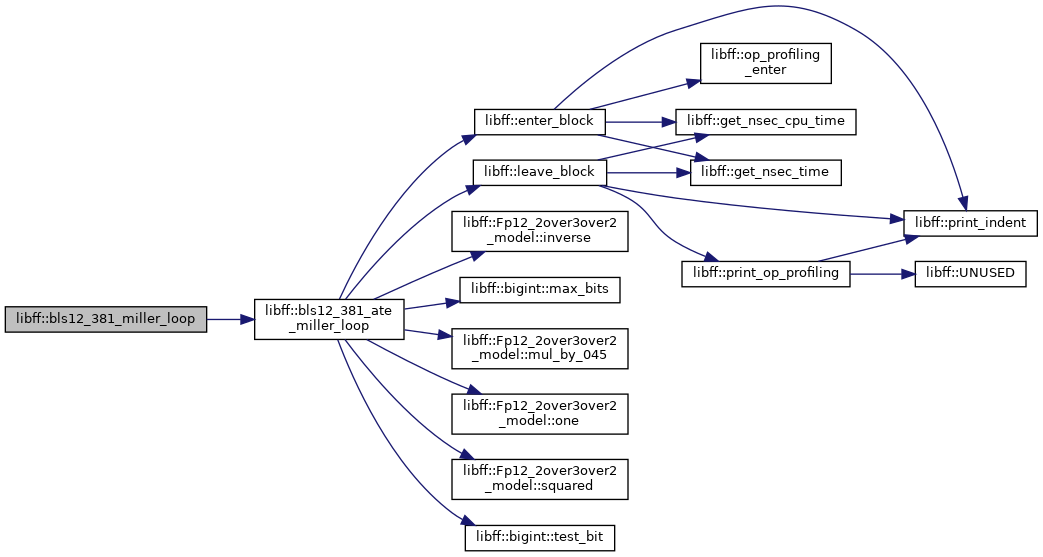
| bls12_381_Fq12 libff::bls12_381_miller_loop | ( | const bls12_381_G1_precomp & | prec_P, |
| const bls12_381_G2_precomp & | prec_Q | ||
| ) |
Definition at line 507 of file bls12_381_pairing.cpp.

◆ bls12_381_mixed_addition_step_for_miller_loop()
| void libff::bls12_381_mixed_addition_step_for_miller_loop | ( | const bls12_381_G2 | base, |
| bls12_381_G2 & | current, | ||
| bls12_381_ate_ell_coeffs & | c | ||
| ) |
Definition at line 274 of file bls12_381_pairing.cpp.


◆ bls12_381_pairing()
| bls12_381_Fq12 libff::bls12_381_pairing | ( | const bls12_381_G1 & | P, |
| const bls12_381_G2 & | Q | ||
| ) |
Definition at line 522 of file bls12_381_pairing.cpp.

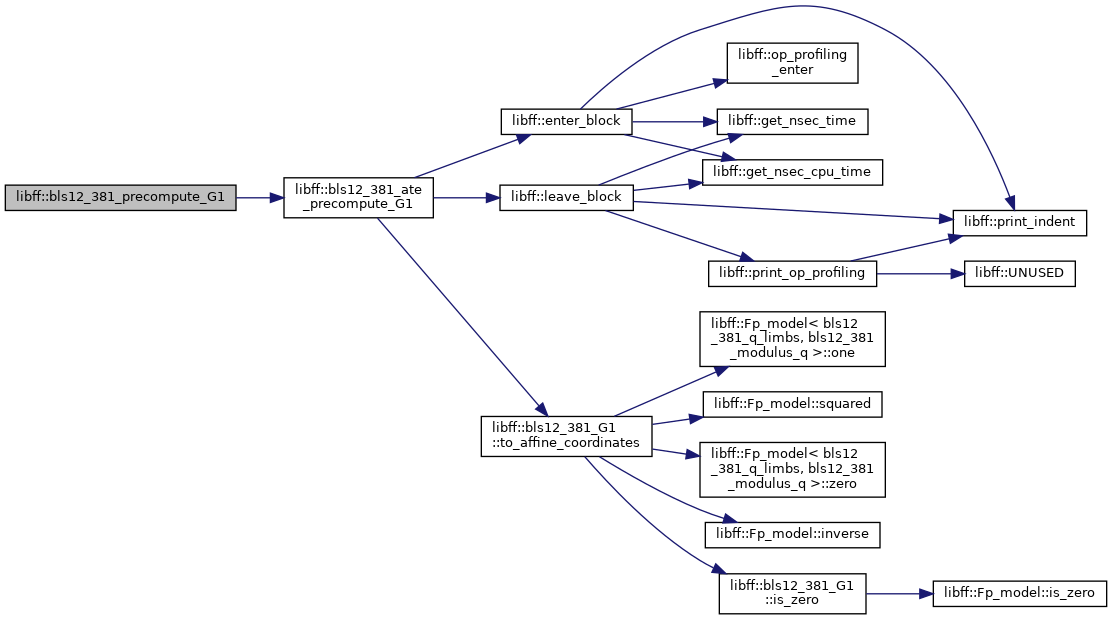
◆ bls12_381_precompute_G1()
| bls12_381_G1_precomp libff::bls12_381_precompute_G1 | ( | const bls12_381_G1 & | P | ) |
Definition at line 497 of file bls12_381_pairing.cpp.

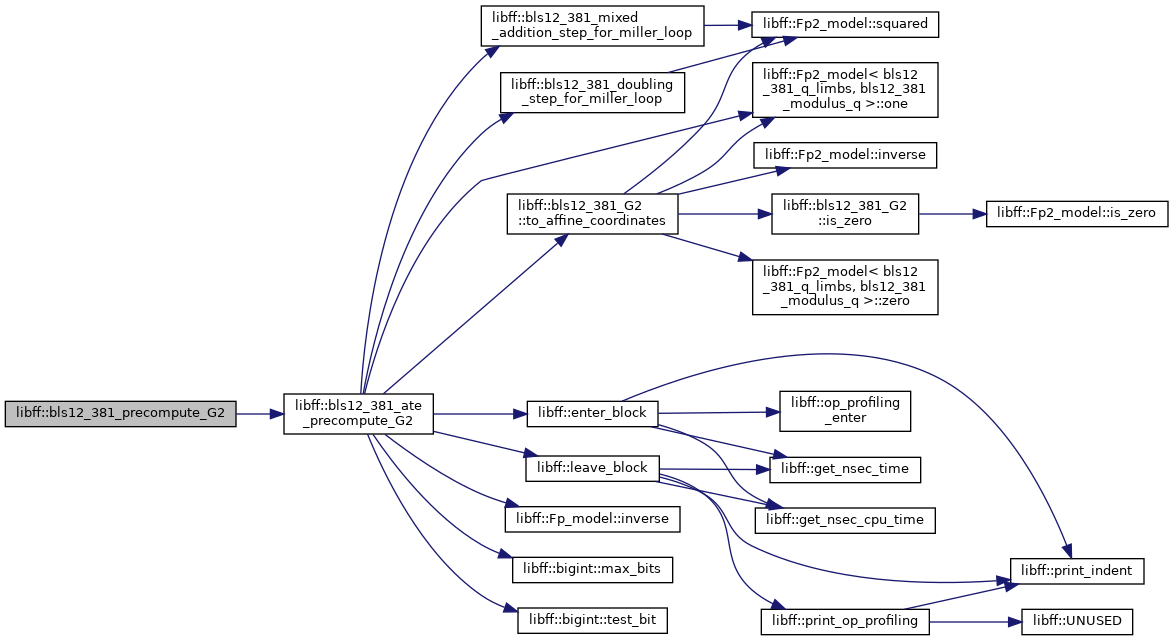
◆ bls12_381_precompute_G2()
| bls12_381_G2_precomp libff::bls12_381_precompute_G2 | ( | const bls12_381_G2 & | Q | ) |
Definition at line 502 of file bls12_381_pairing.cpp.

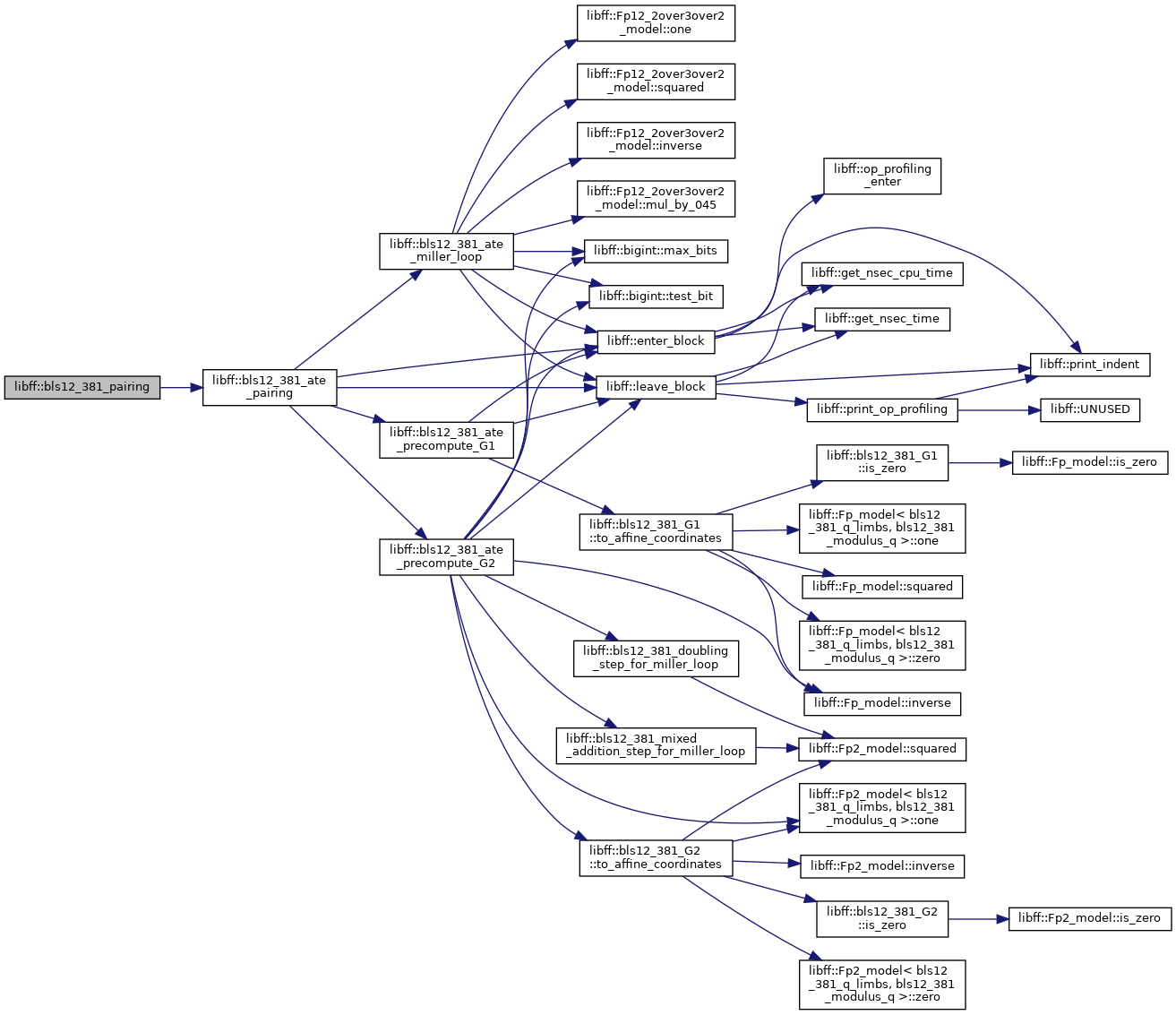
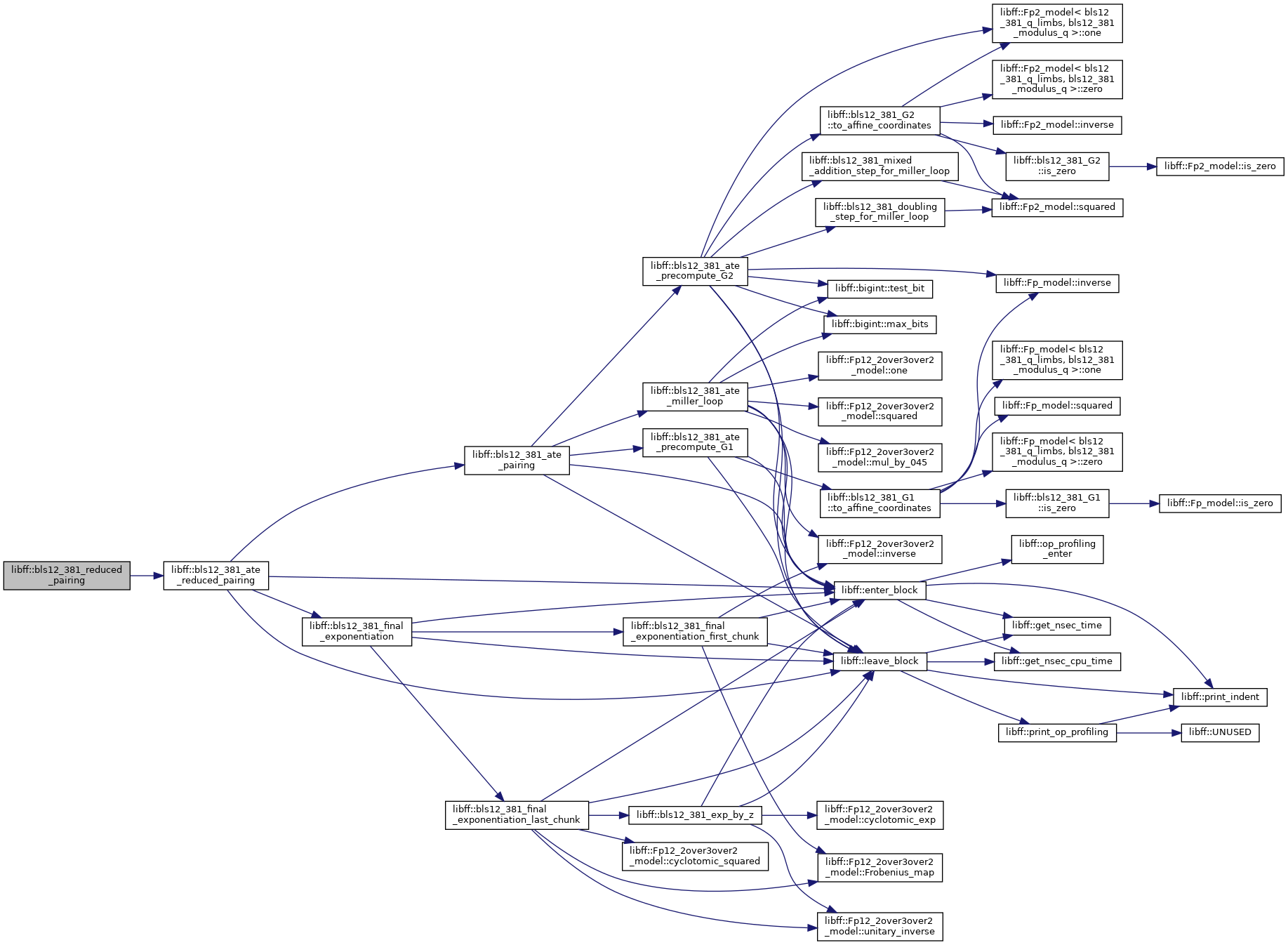
◆ bls12_381_reduced_pairing()
| bls12_381_GT libff::bls12_381_reduced_pairing | ( | const bls12_381_G1 & | P, |
| const bls12_381_G2 & | Q | ||
| ) |
Definition at line 527 of file bls12_381_pairing.cpp.

◆ bn128_ate_miller_loop()
| bn128_Fq12 libff::bn128_ate_miller_loop | ( | const bn128_ate_G1_precomp & | prec_P, |
| const bn128_ate_G2_precomp & | prec_Q | ||
| ) |
◆ bn128_ate_precompute_G1()
| bn128_ate_G1_precomp libff::bn128_ate_precompute_G1 | ( | const bn128_G1 & | P | ) |
Definition at line 166 of file bn128_pairing.cpp.
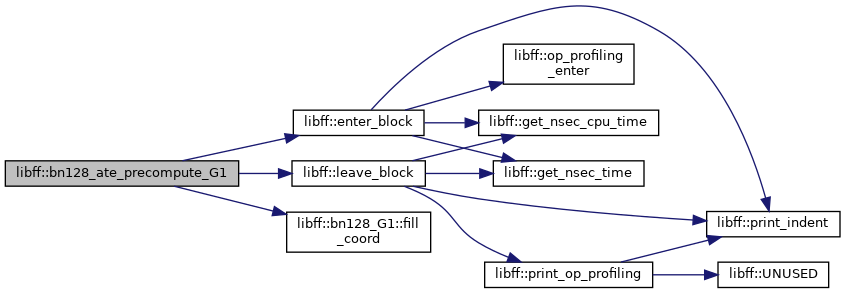

◆ bn128_ate_precompute_G2()
| bn128_ate_G2_precomp libff::bn128_ate_precompute_G2 | ( | const bn128_G2 & | Q | ) |
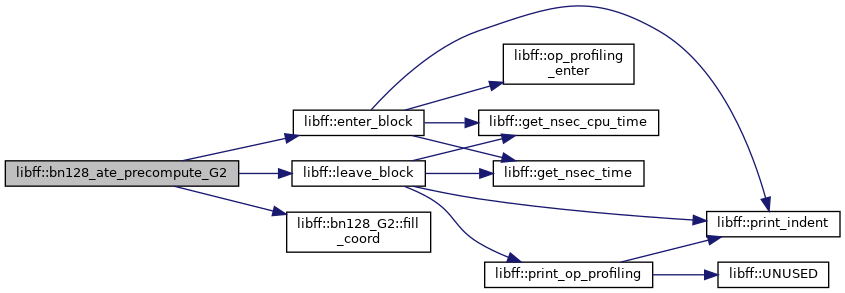
Definition at line 179 of file bn128_pairing.cpp.

◆ bn128_double_ate_miller_loop()
| bn128_Fq12 libff::bn128_double_ate_miller_loop | ( | const bn128_ate_G1_precomp & | prec_P1, |
| const bn128_ate_G2_precomp & | prec_Q1, | ||
| const bn128_ate_G1_precomp & | prec_P2, | ||
| const bn128_ate_G2_precomp & | prec_Q2 | ||
| ) |
◆ bn128_final_exponentiation()
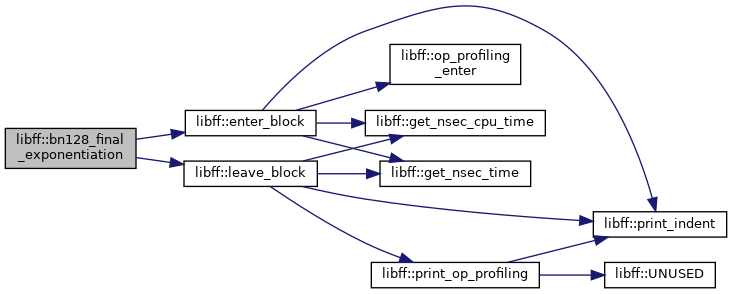
| bn128_GT libff::bn128_final_exponentiation | ( | const bn128_Fq12 & | elt | ) |
Definition at line 212 of file bn128_pairing.cpp.

◆ bn_batch_invert()
| void libff::bn_batch_invert | ( | std::vector< FieldT > & | vec | ) |
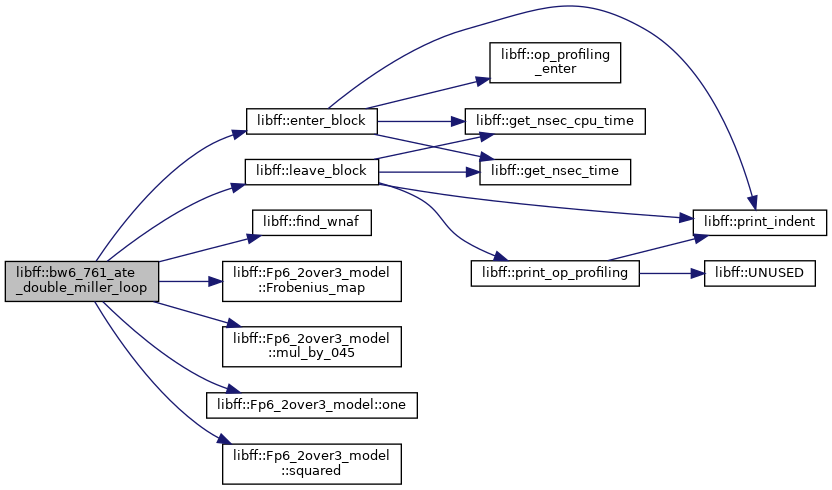
◆ bw6_761_ate_double_miller_loop()
| bw6_761_Fq6 libff::bw6_761_ate_double_miller_loop | ( | const bw6_761_ate_G1_precomp & | prec_P1, |
| const bw6_761_ate_G2_precomp & | prec_Q1, | ||
| const bw6_761_ate_G1_precomp & | prec_P2, | ||
| const bw6_761_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 508 of file bw6_761_pairing.cpp.

◆ bw6_761_ate_miller_loop()
| bw6_761_Fq6 libff::bw6_761_ate_miller_loop | ( | const bw6_761_ate_G1_precomp & | prec_P, |
| const bw6_761_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 423 of file bw6_761_pairing.cpp.

◆ bw6_761_ate_pairing()
| bw6_761_Fq6 libff::bw6_761_ate_pairing | ( | const bw6_761_G1 & | P, |
| const bw6_761_G2 & | Q | ||
| ) |
Definition at line 625 of file bw6_761_pairing.cpp.

◆ bw6_761_ate_precompute_G1()
| bw6_761_ate_G1_precomp libff::bw6_761_ate_precompute_G1 | ( | const bw6_761_G1 & | P | ) |
Definition at line 354 of file bw6_761_pairing.cpp.

◆ bw6_761_ate_precompute_G2()
| bw6_761_ate_G2_precomp libff::bw6_761_ate_precompute_G2 | ( | const bw6_761_G2 & | Q | ) |
◆ bw6_761_ate_reduced_pairing()
| bw6_761_GT libff::bw6_761_ate_reduced_pairing | ( | const bw6_761_G1 & | P, |
| const bw6_761_G2 & | Q | ||
| ) |
Definition at line 635 of file bw6_761_pairing.cpp.

◆ bw6_761_double_miller_loop()
| bw6_761_Fq6 libff::bw6_761_double_miller_loop | ( | const bw6_761_ate_G1_precomp & | prec_P1, |
| const bw6_761_ate_G2_precomp & | prec_Q1, | ||
| const bw6_761_ate_G1_precomp & | prec_P2, | ||
| const bw6_761_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 662 of file bw6_761_pairing.cpp.
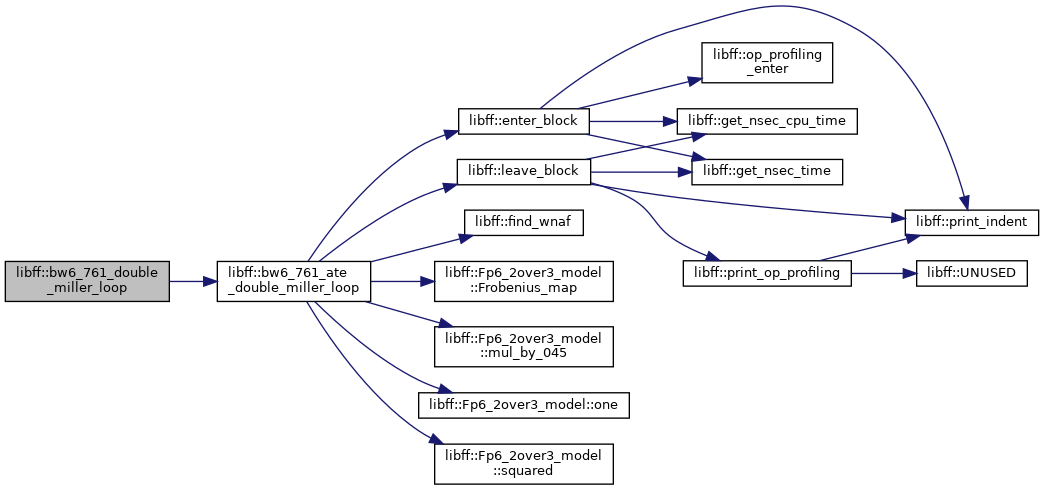

◆ bw6_761_exp_by_z()
| bw6_761_Fq6 libff::bw6_761_exp_by_z | ( | const bw6_761_Fq6 & | elt | ) |
Definition at line 150 of file bw6_761_pairing.cpp.
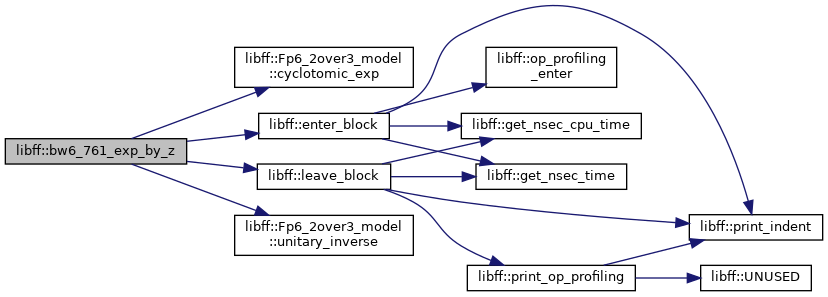

◆ bw6_761_final_exponentiation()
| bw6_761_GT libff::bw6_761_final_exponentiation | ( | const bw6_761_Fq6 & | elt | ) |
Definition at line 258 of file bw6_761_pairing.cpp.
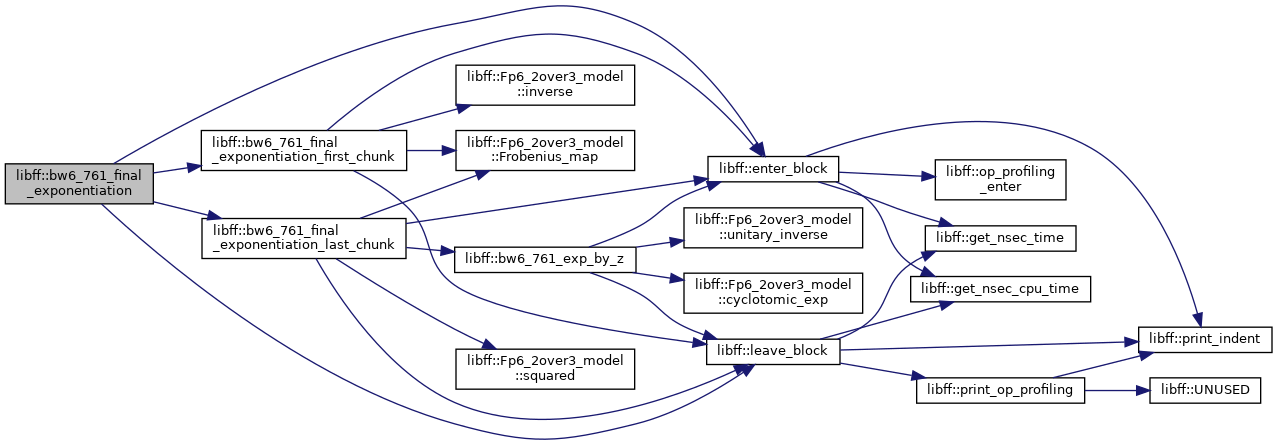

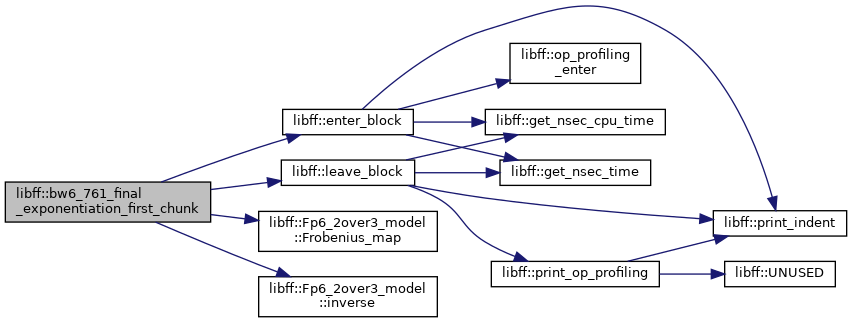
◆ bw6_761_final_exponentiation_first_chunk()
| bw6_761_Fq6 libff::bw6_761_final_exponentiation_first_chunk | ( | const bw6_761_Fq6 & | elt | ) |
Definition at line 131 of file bw6_761_pairing.cpp.

◆ bw6_761_final_exponentiation_last_chunk()
| bw6_761_Fq6 libff::bw6_761_final_exponentiation_last_chunk | ( | const bw6_761_Fq6 & | elt | ) |
Definition at line 172 of file bw6_761_pairing.cpp.
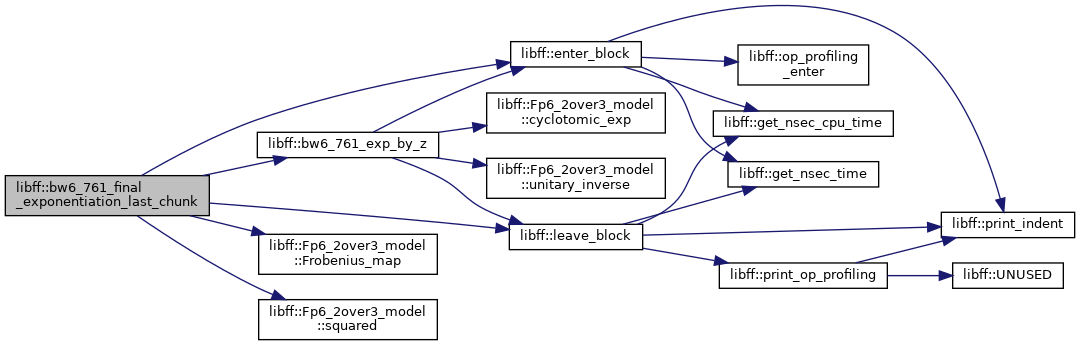

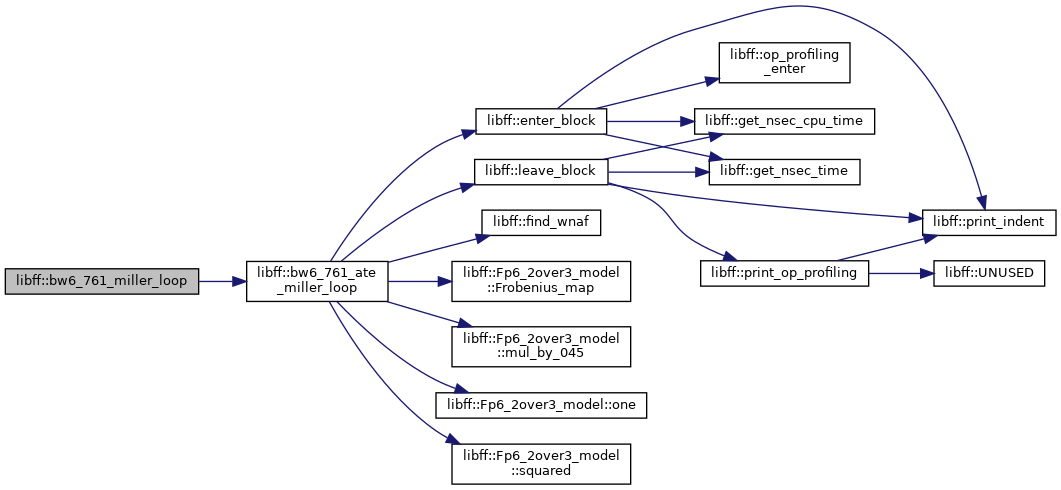
◆ bw6_761_miller_loop()
| bw6_761_Fq6 libff::bw6_761_miller_loop | ( | const bw6_761_G1_precomp & | prec_P, |
| const bw6_761_G2_precomp & | prec_Q | ||
| ) |
Definition at line 656 of file bw6_761_pairing.cpp.

◆ bw6_761_pairing()
| bw6_761_Fq6 libff::bw6_761_pairing | ( | const bw6_761_G1 & | P, |
| const bw6_761_G2 & | Q | ||
| ) |
Definition at line 671 of file bw6_761_pairing.cpp.
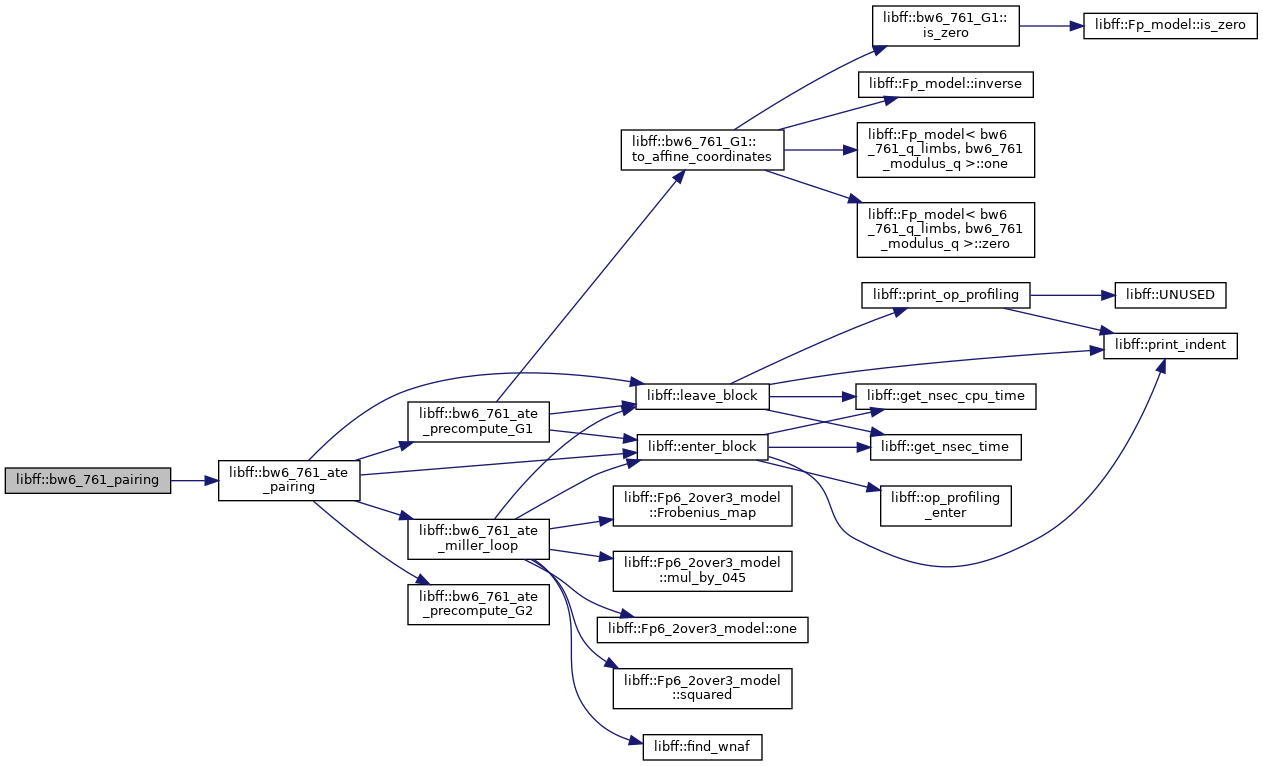

◆ bw6_761_precompute_G1()
| bw6_761_G1_precomp libff::bw6_761_precompute_G1 | ( | const bw6_761_G1 & | P | ) |
Definition at line 646 of file bw6_761_pairing.cpp.
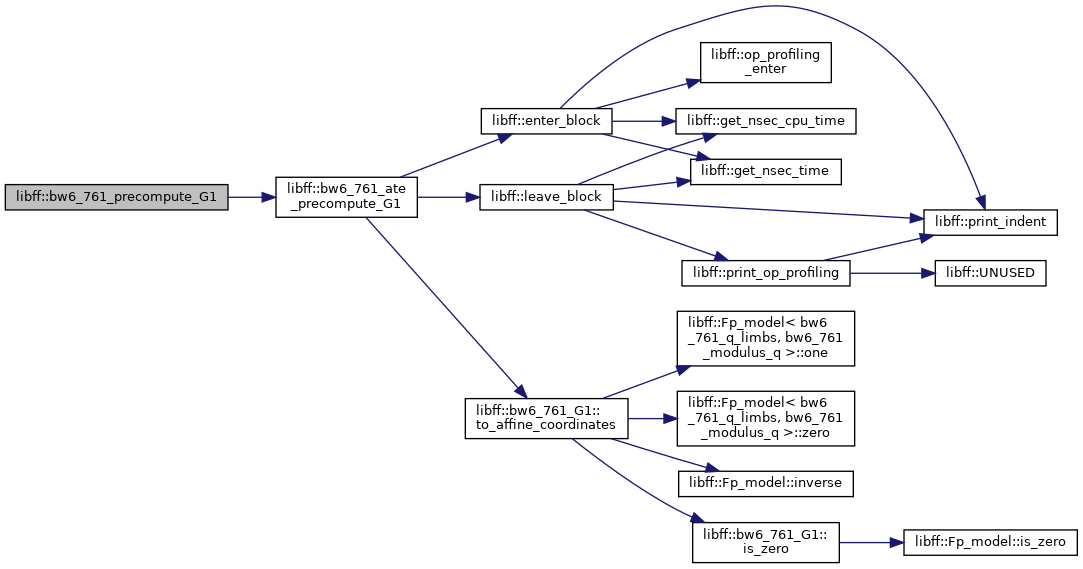

◆ bw6_761_precompute_G2()
| bw6_761_G2_precomp libff::bw6_761_precompute_G2 | ( | const bw6_761_G2 & | Q | ) |
Definition at line 651 of file bw6_761_pairing.cpp.


◆ bw6_761_reduced_pairing()
| bw6_761_GT libff::bw6_761_reduced_pairing | ( | const bw6_761_G1 & | P, |
| const bw6_761_G2 & | Q | ||
| ) |
Definition at line 676 of file bw6_761_pairing.cpp.
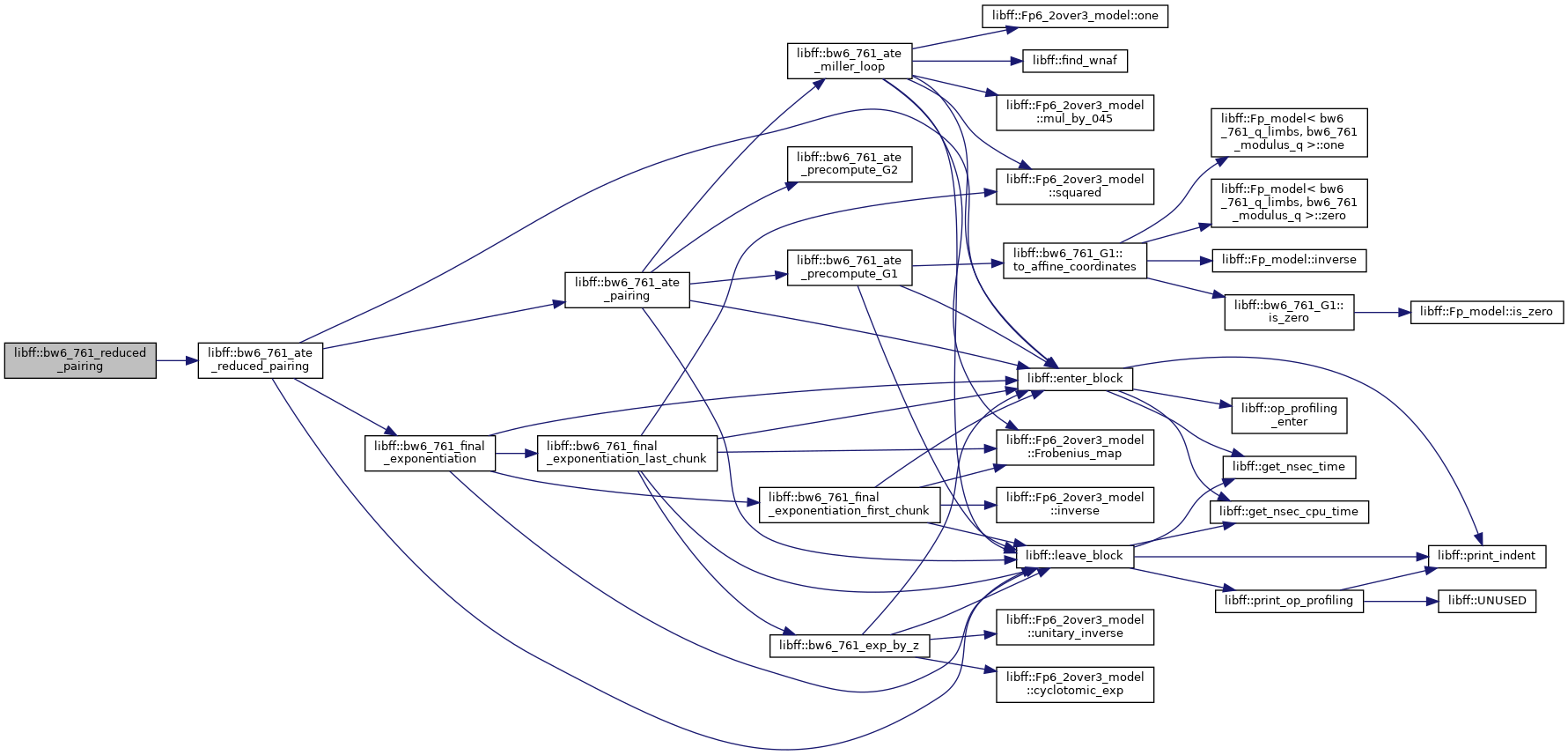

◆ bytes_to_hex_reversed()
| std::string libff::bytes_to_hex_reversed | ( | const void * | bytes, |
| size_t | num_bytes, | ||
| bool | prefix | ||
| ) |
◆ char_to_nibble()
| uint8_t libff::char_to_nibble | ( | const char | c | ) |
Definition at line 19 of file serialization.cpp.
◆ clear_profiling_counters()
| void libff::clear_profiling_counters | ( | ) |
Definition at line 110 of file profiling.cpp.
◆ consume_newline()
|
inline |

◆ consume_OUTPUT_NEWLINE()
|
inline |

◆ consume_OUTPUT_SEPARATOR()
|
inline |
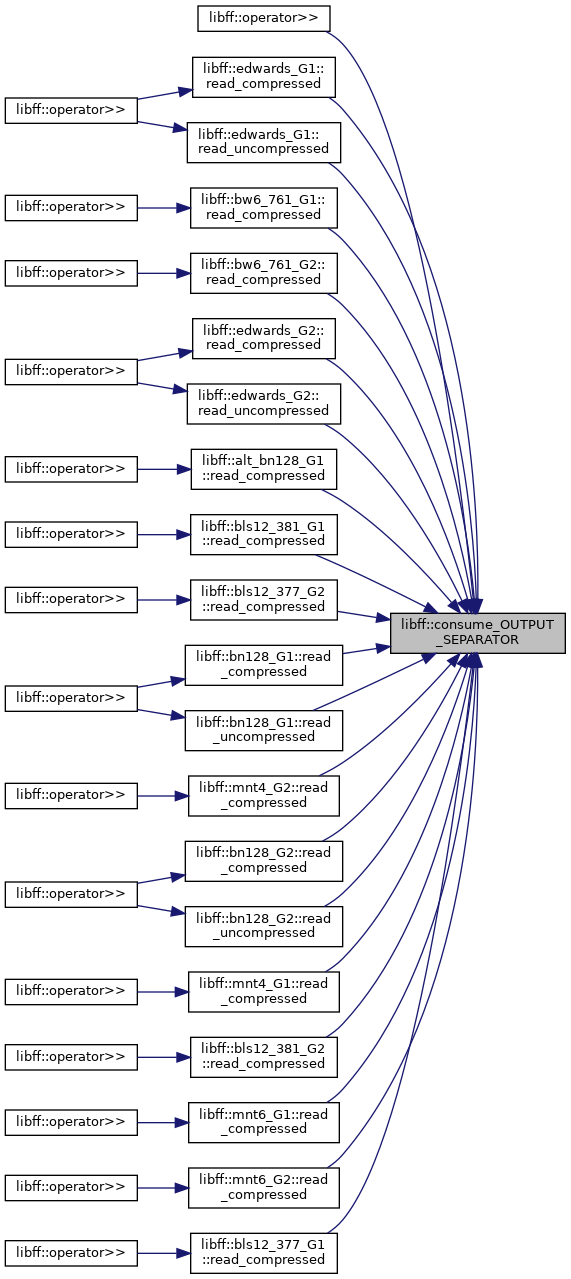
◆ convert_bit_vector_to_field_element()
| FieldT libff::convert_bit_vector_to_field_element | ( | const bit_vector & | v | ) |
◆ convert_bit_vector_to_field_element_vector()
| std::vector<FieldT> libff::convert_bit_vector_to_field_element_vector | ( | const bit_vector & | v | ) |
◆ convert_field_element_to_bit_vector() [1/2]
| bit_vector libff::convert_field_element_to_bit_vector | ( | const FieldT & | el | ) |
◆ convert_field_element_to_bit_vector() [2/2]
| bit_vector libff::convert_field_element_to_bit_vector | ( | const FieldT & | el, |
| const size_t | bitcount | ||
| ) |
◆ convert_field_element_vector_to_bit_vector()
| bit_vector libff::convert_field_element_vector_to_bit_vector | ( | const std::vector< FieldT > & | v | ) |
◆ deserialize_bit_vector()
| void libff::deserialize_bit_vector | ( | std::istream & | in, |
| bit_vector & | v | ||
| ) |
◆ div_ceil()
| long long libff::div_ceil | ( | long long | x, |
| long long | y | ||
| ) |
◆ doubling_step_for_flipped_miller_loop() [1/4]
| void libff::doubling_step_for_flipped_miller_loop | ( | const alt_bn128_Fq | two_inv, |
| alt_bn128_G2 & | current, | ||
| alt_bn128_ate_ell_coeffs & | c | ||
| ) |
Definition at line 246 of file alt_bn128_pairing.cpp.

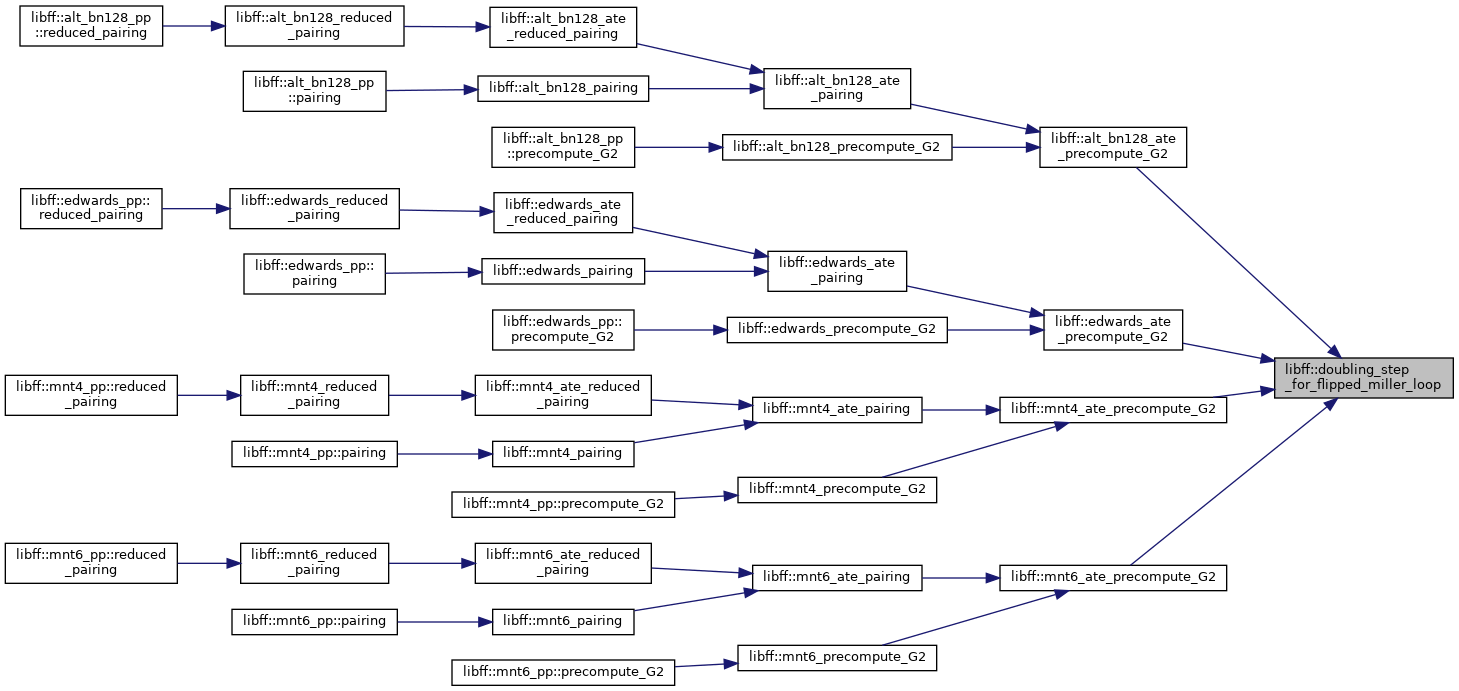
◆ doubling_step_for_flipped_miller_loop() [2/4]
| void libff::doubling_step_for_flipped_miller_loop | ( | extended_edwards_G2_projective & | current, |
| edwards_Fq3_conic_coefficients & | cc | ||
| ) |
◆ doubling_step_for_flipped_miller_loop() [3/4]
| void libff::doubling_step_for_flipped_miller_loop | ( | extended_mnt4_G2_projective & | current, |
| mnt4_ate_dbl_coeffs & | dc | ||
| ) |
◆ doubling_step_for_flipped_miller_loop() [4/4]
| void libff::doubling_step_for_flipped_miller_loop | ( | extended_mnt6_G2_projective & | current, |
| mnt6_ate_dbl_coeffs & | dc | ||
| ) |
◆ doubling_step_for_miller_loop() [1/2]
| void libff::doubling_step_for_miller_loop | ( | bw6_761_G2 & | current, |
| bw6_761_ate_ell_coeffs & | c | ||
| ) |
Definition at line 274 of file bw6_761_pairing.cpp.


◆ doubling_step_for_miller_loop() [2/2]
| void libff::doubling_step_for_miller_loop | ( | extended_edwards_G1_projective & | current, |
| edwards_Fq_conic_coefficients & | cc | ||
| ) |
◆ edwards_ate_double_miller_loop()
| edwards_Fq6 libff::edwards_ate_double_miller_loop | ( | const edwards_ate_G1_precomp & | prec_P1, |
| const edwards_ate_G2_precomp & | prec_Q1, | ||
| const edwards_ate_G1_precomp & | prec_P2, | ||
| const edwards_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 702 of file edwards_pairing.cpp.
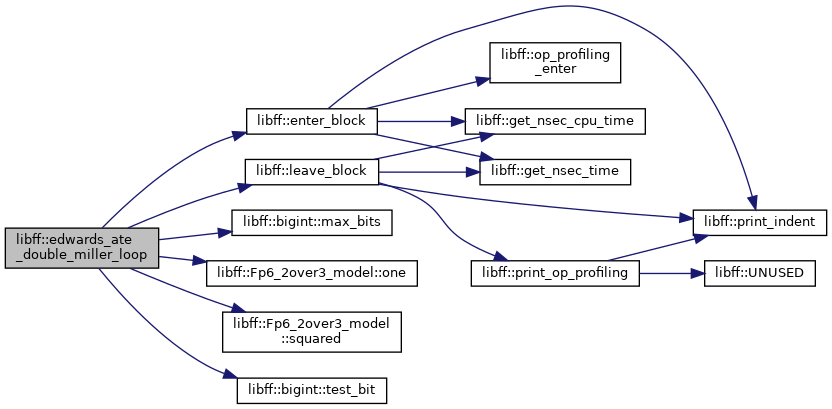

◆ edwards_ate_miller_loop()
| edwards_Fq6 libff::edwards_ate_miller_loop | ( | const edwards_ate_G1_precomp & | prec_P, |
| const edwards_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 662 of file edwards_pairing.cpp.
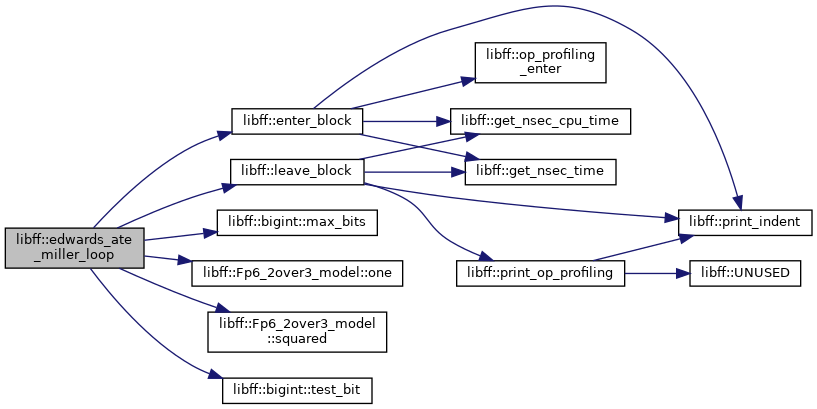

◆ edwards_ate_pairing()
| edwards_Fq6 libff::edwards_ate_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
Definition at line 757 of file edwards_pairing.cpp.
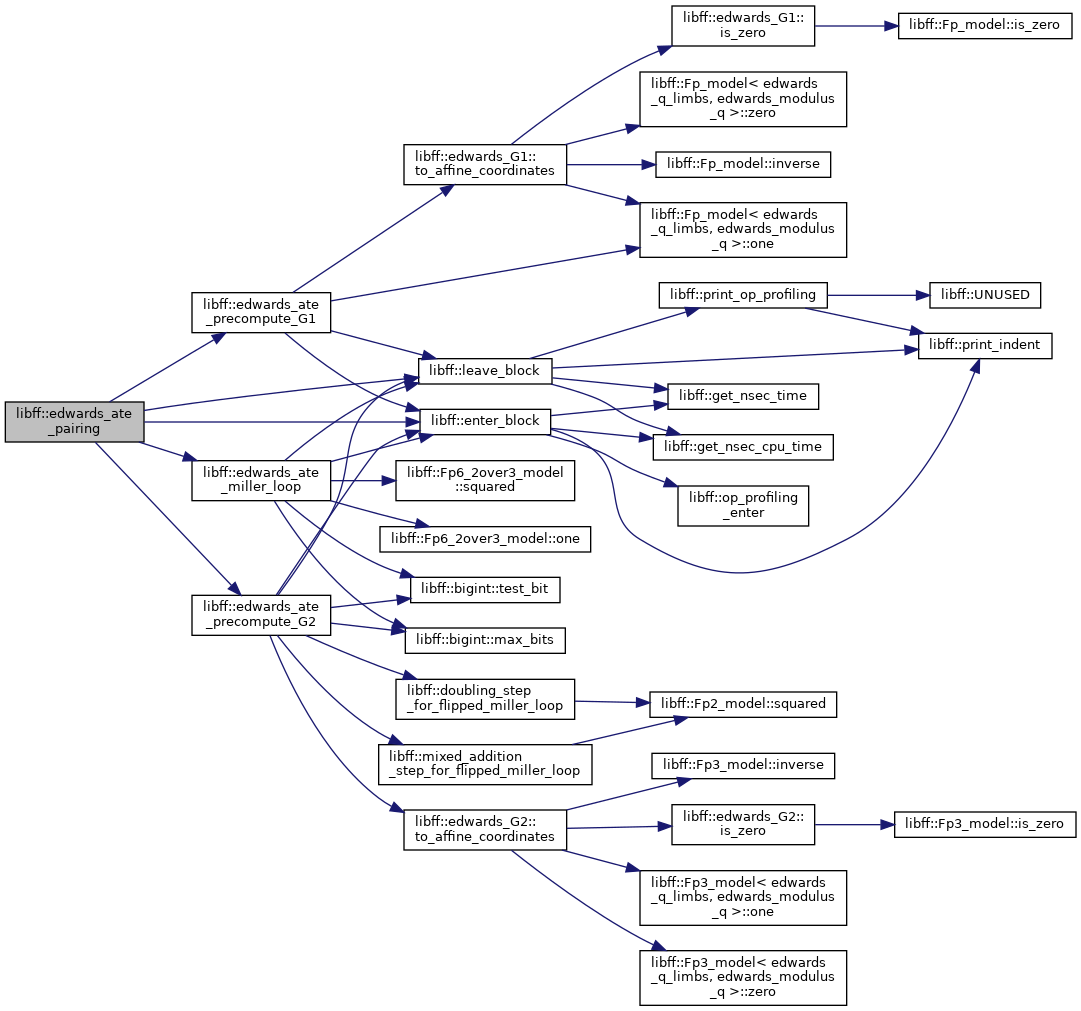

◆ edwards_ate_precompute_G1()
| edwards_ate_G1_precomp libff::edwards_ate_precompute_G1 | ( | const edwards_G1 & | P | ) |
Definition at line 609 of file edwards_pairing.cpp.
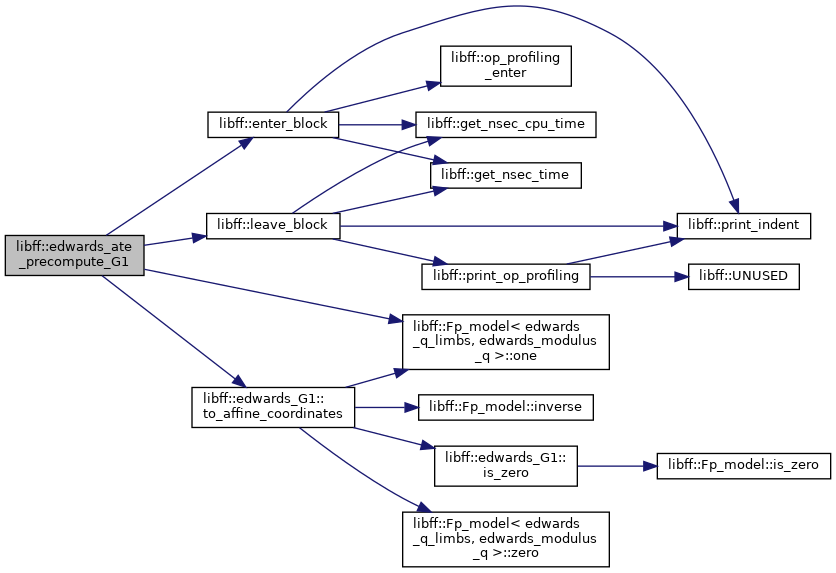

◆ edwards_ate_precompute_G2()
| edwards_ate_G2_precomp libff::edwards_ate_precompute_G2 | ( | const edwards_G2 & | Q | ) |
Definition at line 623 of file edwards_pairing.cpp.
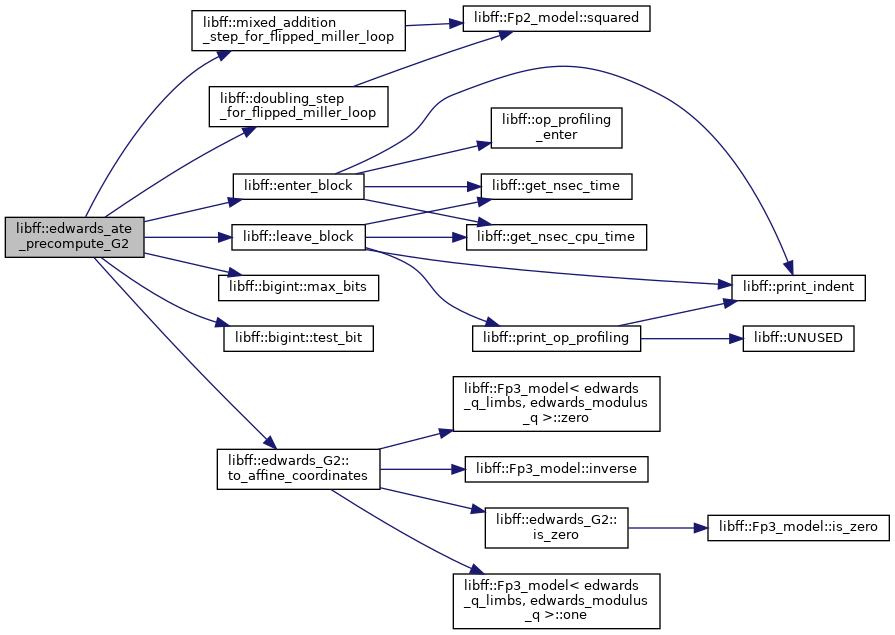

◆ edwards_ate_reduced_pairing()
| edwards_GT libff::edwards_ate_reduced_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
Definition at line 767 of file edwards_pairing.cpp.
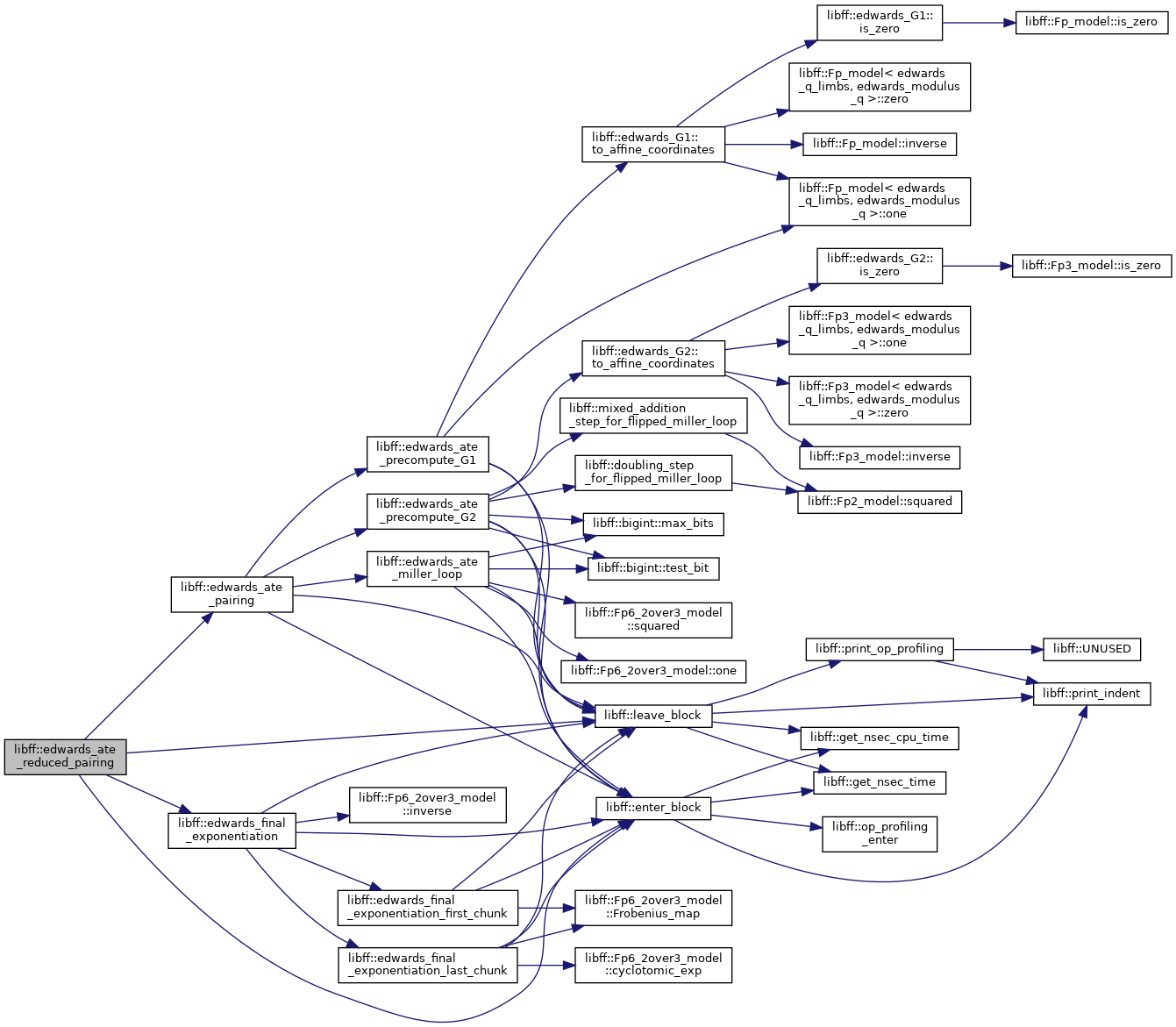

◆ edwards_double_miller_loop()
| edwards_Fq6 libff::edwards_double_miller_loop | ( | const edwards_G1_precomp & | prec_P1, |
| const edwards_G2_precomp & | prec_Q1, | ||
| const edwards_G1_precomp & | prec_P2, | ||
| const edwards_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 792 of file edwards_pairing.cpp.
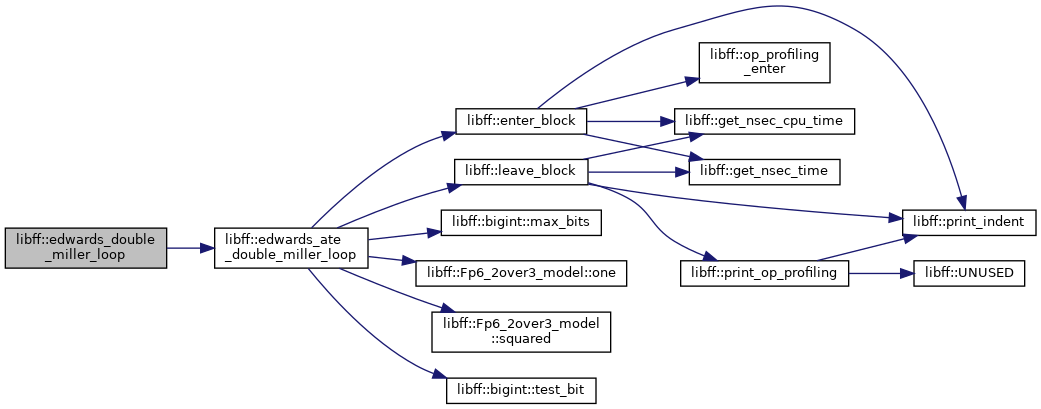

◆ edwards_final_exponentiation()
| edwards_GT libff::edwards_final_exponentiation | ( | const edwards_Fq6 & | elt | ) |
Definition at line 219 of file edwards_pairing.cpp.
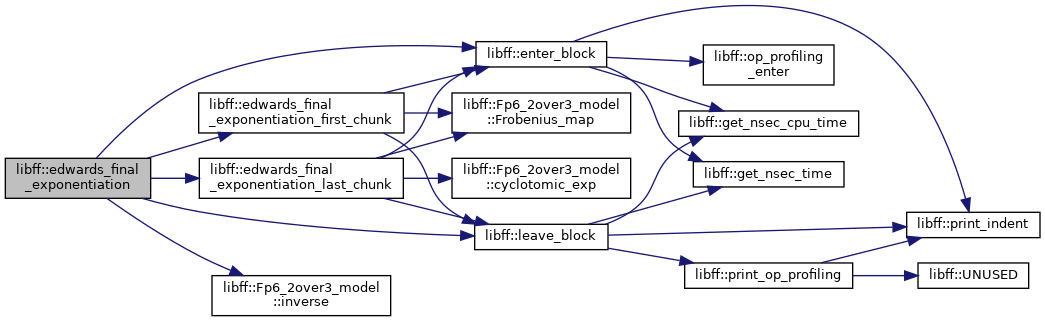
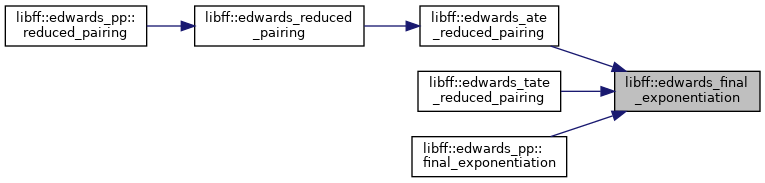
◆ edwards_final_exponentiation_first_chunk()
| edwards_Fq6 libff::edwards_final_exponentiation_first_chunk | ( | const edwards_Fq6 & | elt, |
| const edwards_Fq6 & | elt_inv | ||
| ) |
Definition at line 200 of file edwards_pairing.cpp.
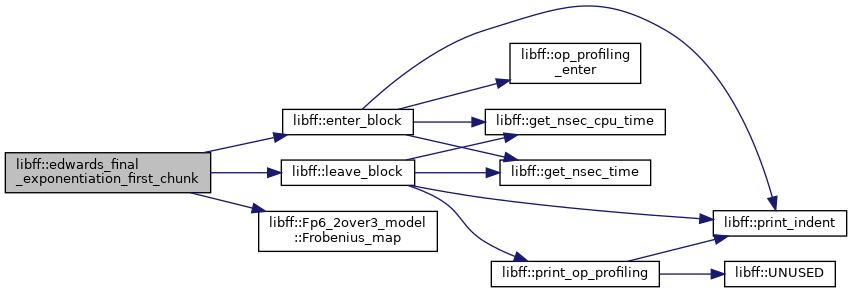

◆ edwards_final_exponentiation_last_chunk()
| edwards_Fq6 libff::edwards_final_exponentiation_last_chunk | ( | const edwards_Fq6 & | elt, |
| const edwards_Fq6 & | elt_inv | ||
| ) |
Definition at line 179 of file edwards_pairing.cpp.
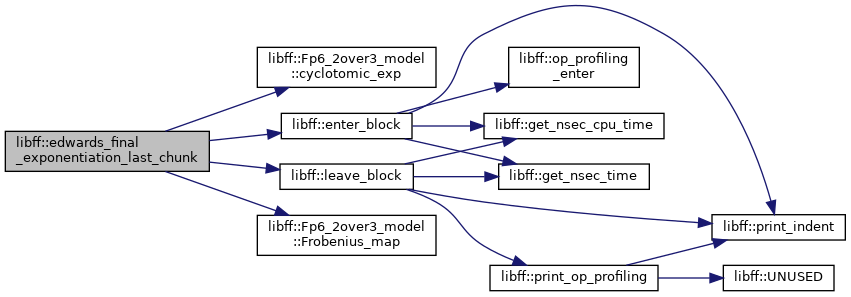

◆ edwards_miller_loop()
| edwards_Fq6 libff::edwards_miller_loop | ( | const edwards_G1_precomp & | prec_P, |
| const edwards_G2_precomp & | prec_Q | ||
| ) |
Definition at line 786 of file edwards_pairing.cpp.
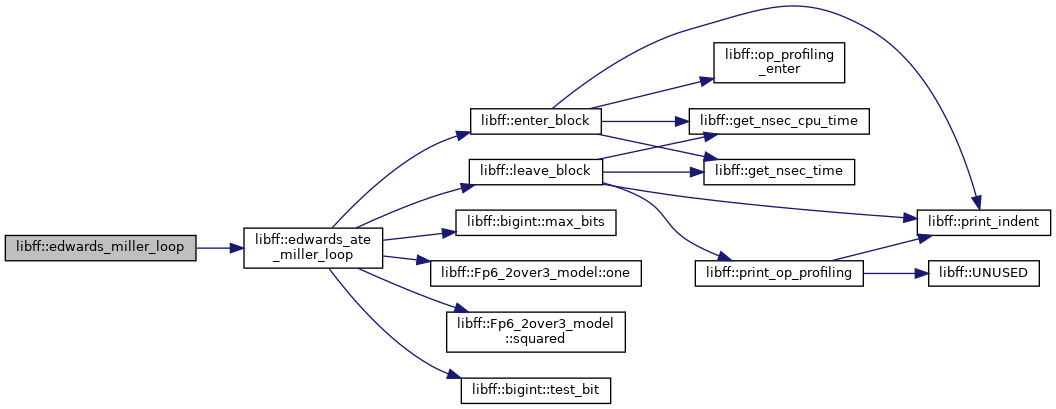

◆ edwards_pairing()
| edwards_Fq6 libff::edwards_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
Definition at line 801 of file edwards_pairing.cpp.
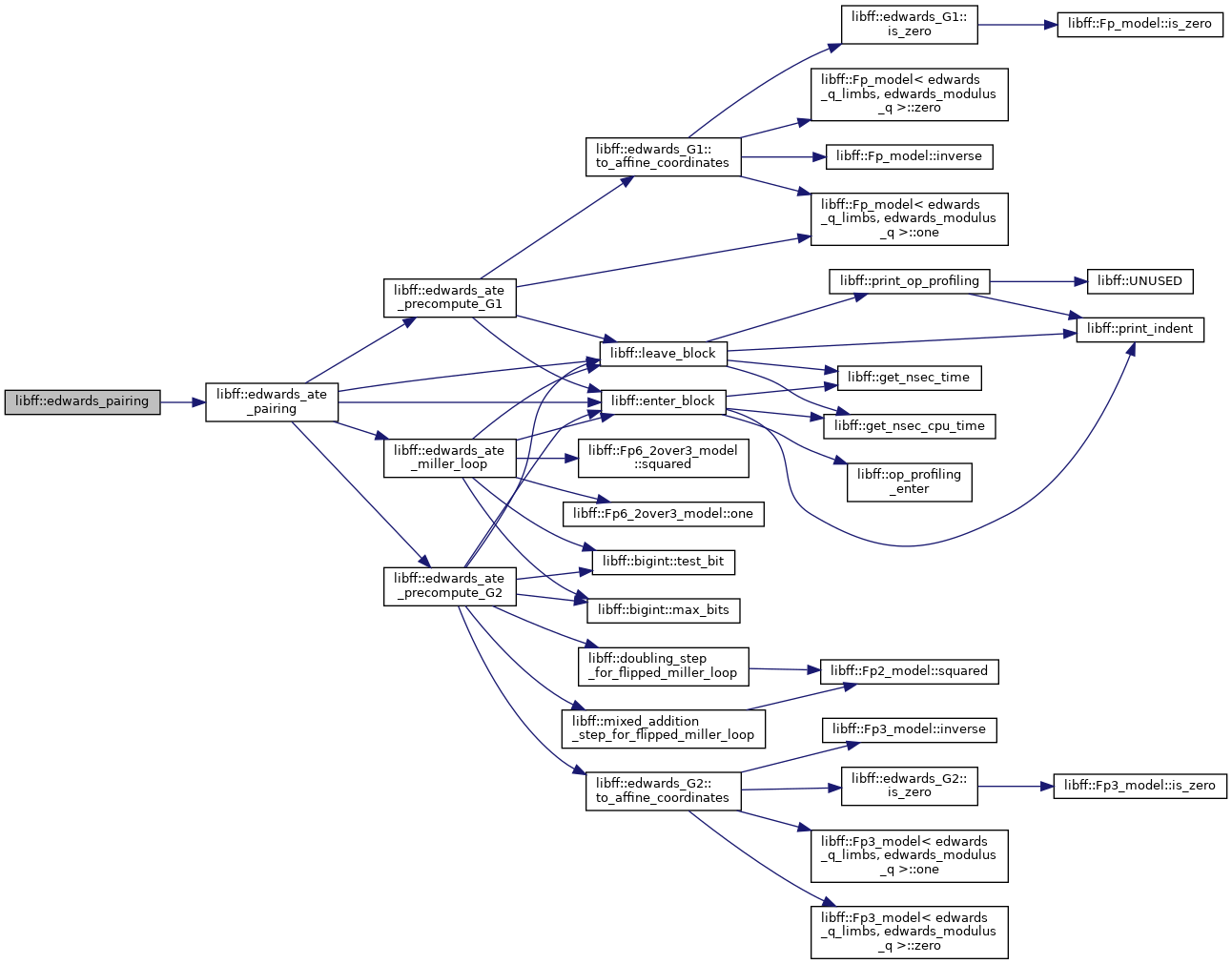

◆ edwards_precompute_G1()
| edwards_G1_precomp libff::edwards_precompute_G1 | ( | const edwards_G1 & | P | ) |
Definition at line 776 of file edwards_pairing.cpp.
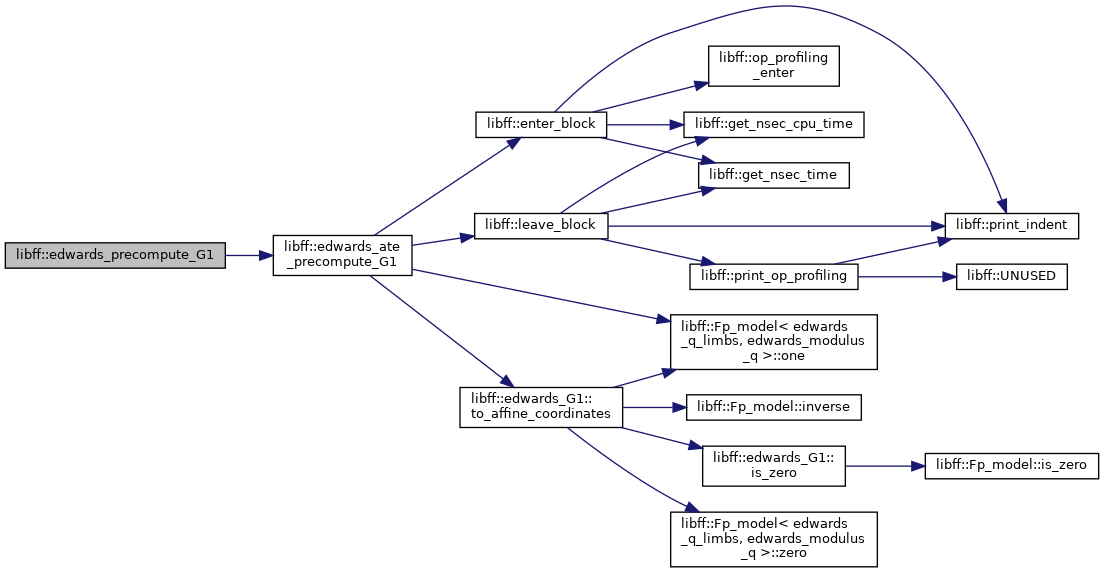

◆ edwards_precompute_G2()
| edwards_G2_precomp libff::edwards_precompute_G2 | ( | const edwards_G2 & | Q | ) |
Definition at line 781 of file edwards_pairing.cpp.
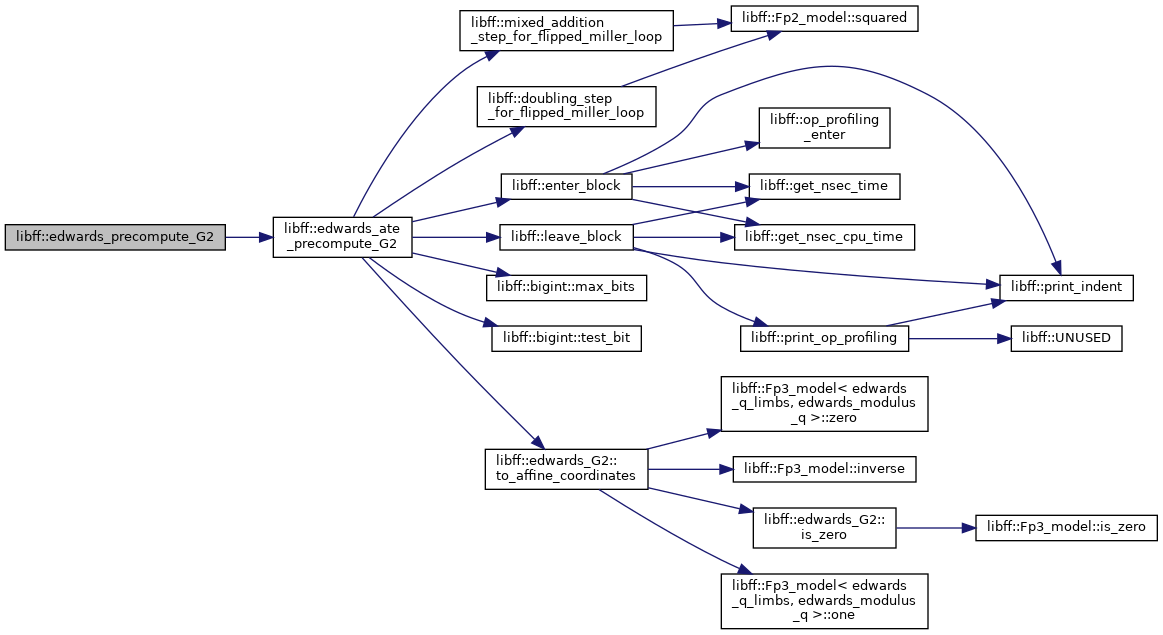

◆ edwards_reduced_pairing()
| edwards_GT libff::edwards_reduced_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
Definition at line 806 of file edwards_pairing.cpp.
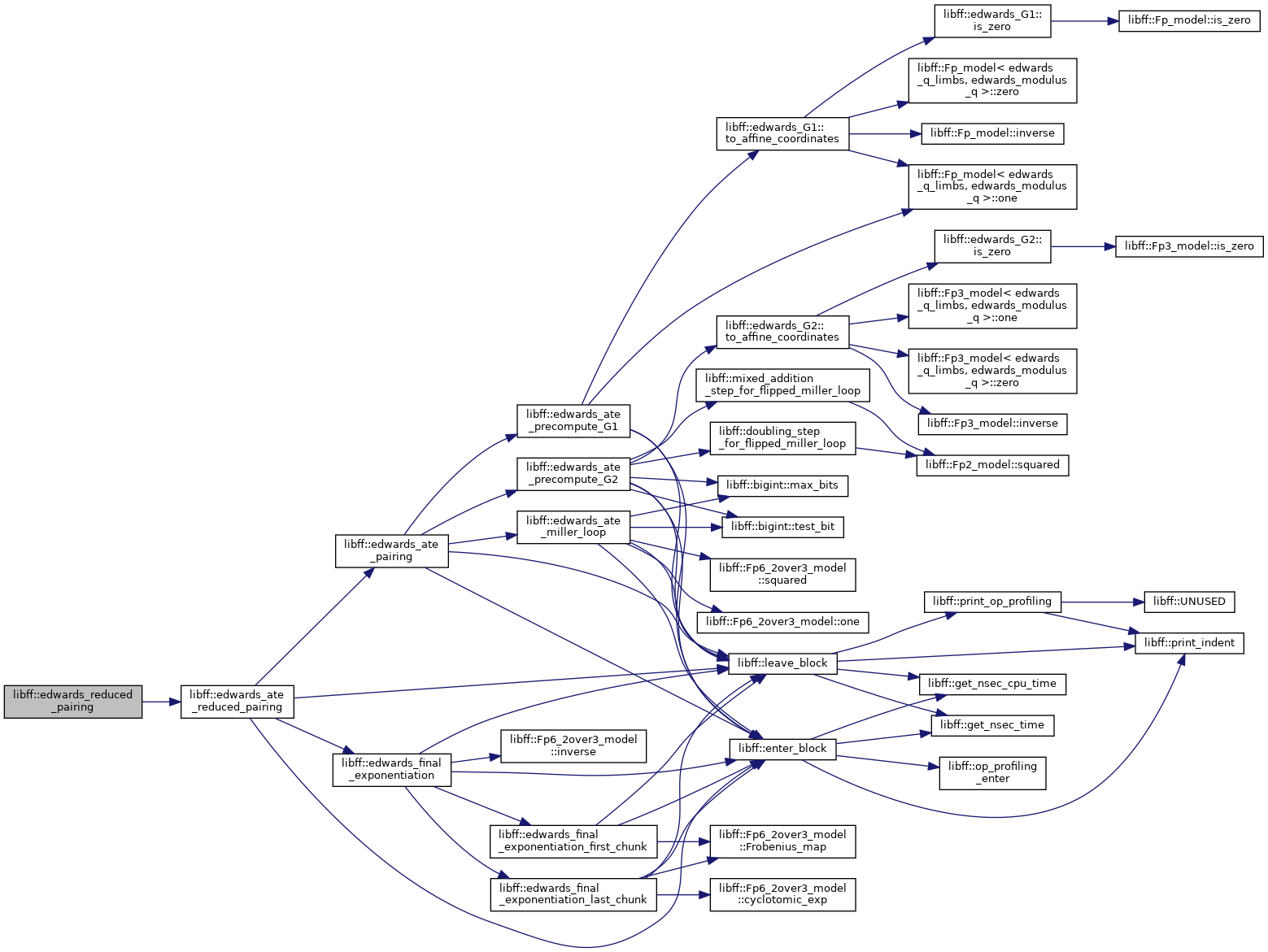

◆ edwards_tate_miller_loop()
| edwards_Fq6 libff::edwards_tate_miller_loop | ( | const edwards_tate_G1_precomp & | prec_P, |
| const edwards_tate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 409 of file edwards_pairing.cpp.
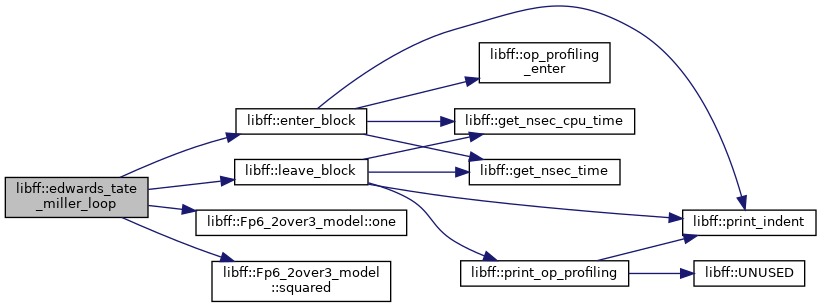

◆ edwards_tate_pairing()
| edwards_Fq6 libff::edwards_tate_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
Definition at line 451 of file edwards_pairing.cpp.
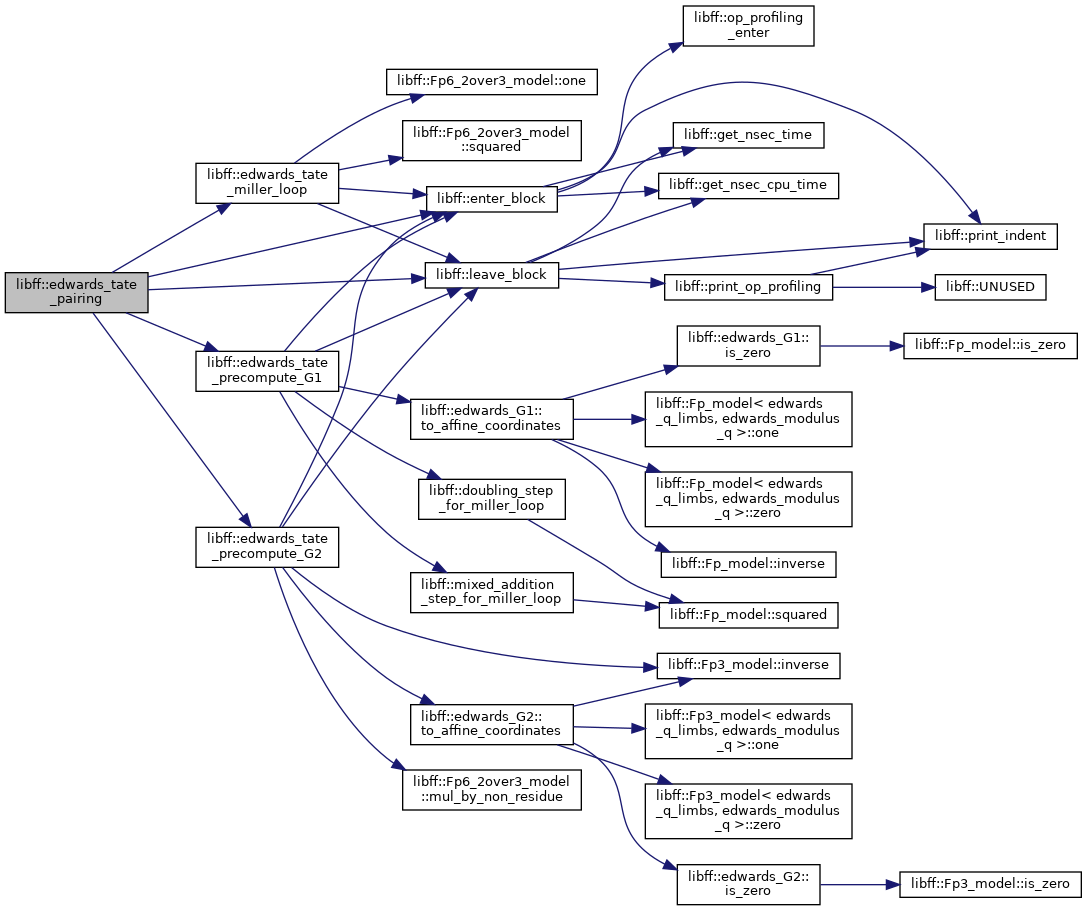

◆ edwards_tate_precompute_G1()
| edwards_tate_G1_precomp libff::edwards_tate_precompute_G1 | ( | const edwards_G1 & | P | ) |
Definition at line 367 of file edwards_pairing.cpp.
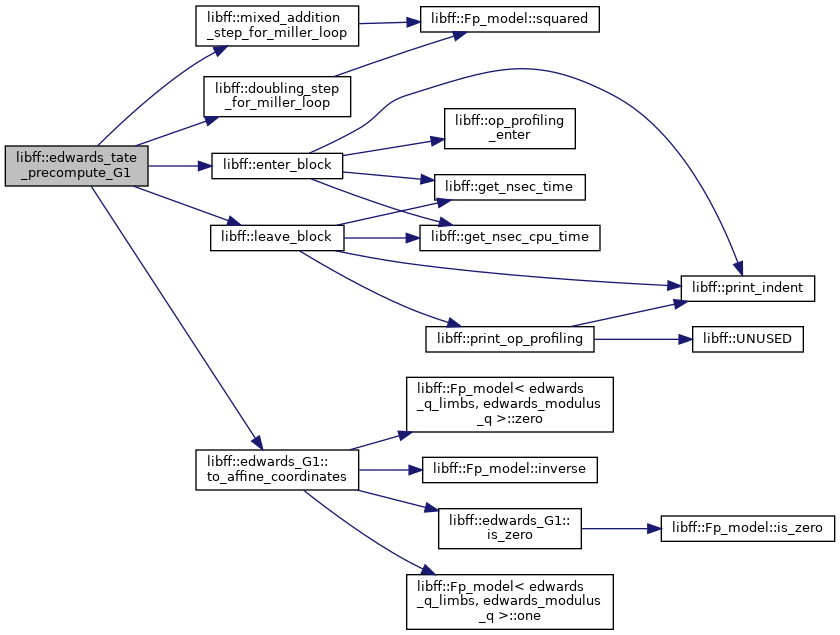

◆ edwards_tate_precompute_G2()
| edwards_tate_G2_precomp libff::edwards_tate_precompute_G2 | ( | const edwards_G2 & | Q | ) |
Definition at line 234 of file edwards_pairing.cpp.
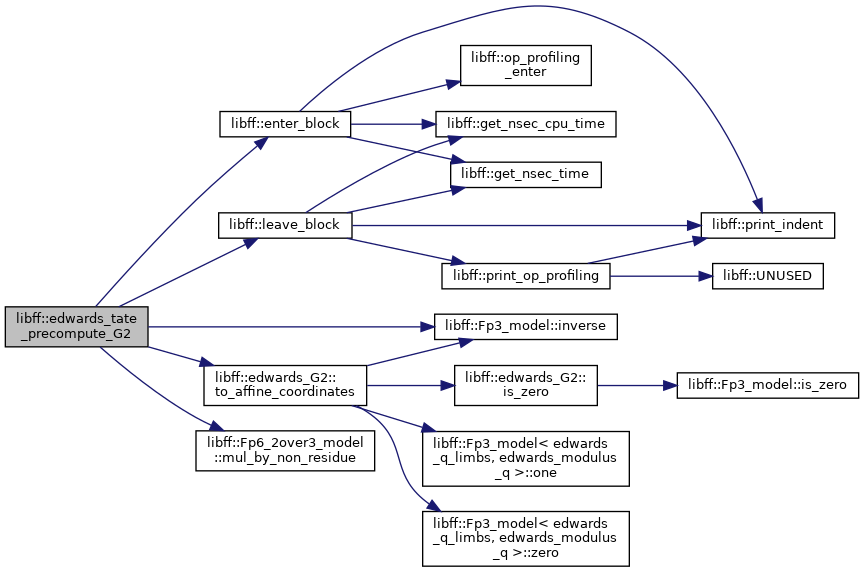

◆ edwards_tate_reduced_pairing()
| edwards_GT libff::edwards_tate_reduced_pairing | ( | const edwards_G1 & | P, |
| const edwards_G2 & | Q | ||
| ) |
◆ enter_block()
| void libff::enter_block | ( | const std::string & | msg, |
| const bool | indent | ||
| ) |
◆ exp2()
|
inline |
◆ field_get_component_0()
| const FieldT::my_Fp& libff::field_get_component_0 | ( | const FieldT & | v | ) |
Rerturns a reference to the 0-th component of the element (or the element itself if FieldT is not an extension field).
◆ field_get_digit()
| size_t libff::field_get_digit | ( | const bigint< n > & | v, |
| const size_t | digit_size, | ||
| const size_t | digit_index | ||
| ) |
Decompose v into fixed-size digits of digit_size bits each.
◆ field_get_signed_digit()
| ssize_t libff::field_get_signed_digit | ( | const bigint< n > & | v, |
| const size_t | digit_size, | ||
| const size_t | digit_index | ||
| ) |
Decompose v into fixed-size signed digits of digit_size bits each.
◆ field_get_signed_digits()
| void libff::field_get_signed_digits | ( | std::vector< ssize_t > & | digits, |
| const FieldT & | v, | ||
| const size_t | digit_size, | ||
| const size_t | num_digits | ||
| ) |
Decompose the input into a (pre-allocated) vector of fixed-size signed digits, of size digit_size bits.
◆ field_read()
| void libff::field_read | ( | FieldT & | v, |
| std::istream & | in_s | ||
| ) |
◆ field_write()
| void libff::field_write | ( | const FieldT & | v, |
| std::ostream & | out_s | ||
| ) |
◆ find_wnaf()
| std::vector<long> libff::find_wnaf | ( | const size_t | window_size, |
| const bigint< n > & | scalar | ||
| ) |
Find the wNAF representation of the given scalar relative to the given window size.
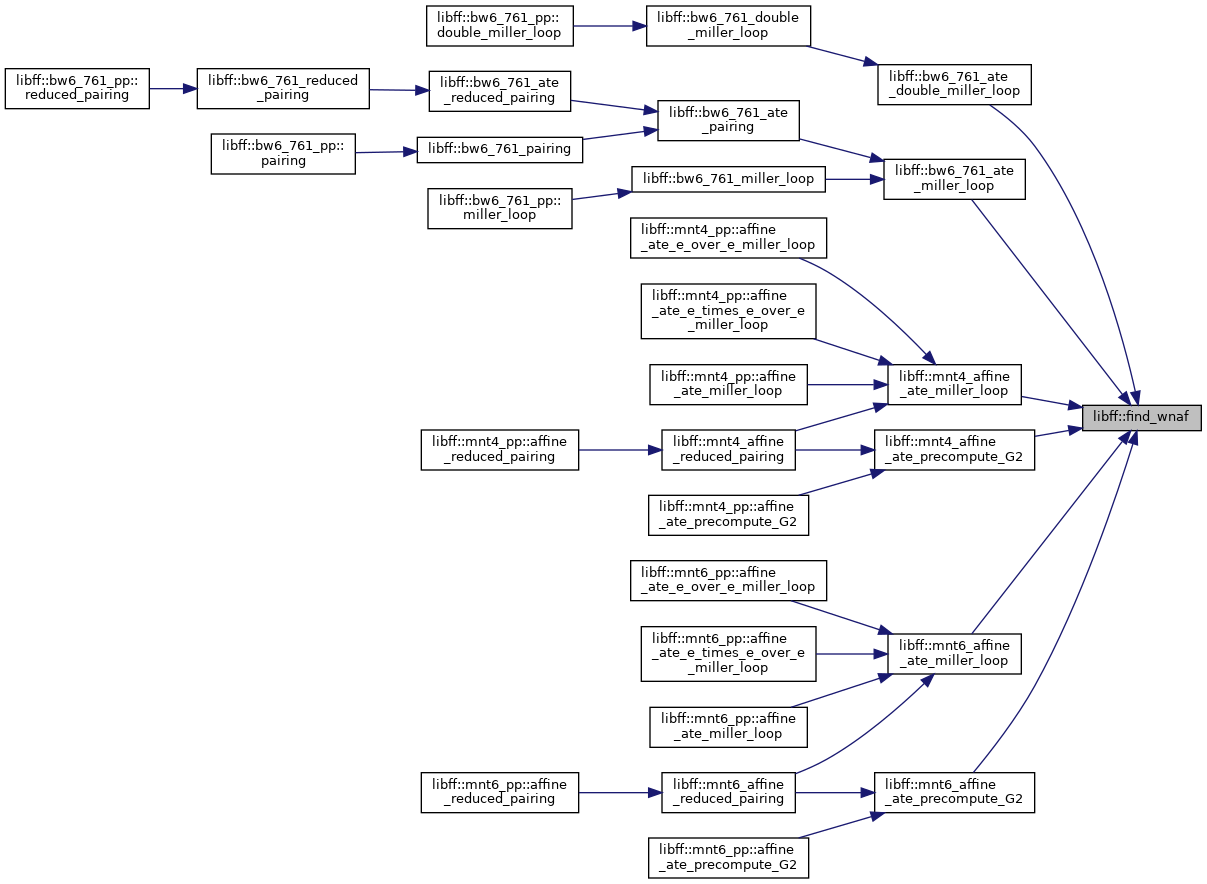
◆ fixed_window_wnaf_exp() [1/2]
| T libff::fixed_window_wnaf_exp | ( | const size_t | window_size, |
| const T & | base, | ||
| const bigint< n > & | scalar | ||
| ) |
In additive notation, use wNAF exponentiation (with the given window size) to compute scalar * base.
◆ fixed_window_wnaf_exp() [2/2]
| T libff::fixed_window_wnaf_exp | ( | const size_t | window_size, |
| const T & | base, | ||
| const std::vector< long > & | naf | ||
| ) |
In additive notation, use wNAF exponentiation (with the given window size) to compute scalar * base, for a scalar in NAF form.
◆ FORMAT()
| std::string libff::FORMAT | ( | const std::string & | prefix, |
| const char * | format, | ||
| ... | |||
| ) |
◆ fp_from_fp()
| void libff::fp_from_fp | ( | Fp_model< wn, wmodulus > & | wfp, |
| const Fp_model< nn, nmodulus > & | nfp | ||
| ) |
Safe conversion from one finite field type to another. Internally asserts that the transformation is injective (i.e. multiple input values cannot result in the same output value).
◆ from_twos_complement()
| int libff::from_twos_complement | ( | size_t | i, |
| size_t | w | ||
| ) |
◆ full_addition_step_for_flipped_miller_loop()
| void libff::full_addition_step_for_flipped_miller_loop | ( | const extended_edwards_G2_projective & | base, |
| extended_edwards_G2_projective & | current, | ||
| edwards_Fq3_conic_coefficients & | cc | ||
| ) |
◆ full_addition_step_for_miller_loop()
| void libff::full_addition_step_for_miller_loop | ( | const extended_edwards_G1_projective & | base, |
| extended_edwards_G1_projective & | current, | ||
| edwards_Fq_conic_coefficients & | cc | ||
| ) |
◆ g1_curve_point_at_x()
| GroupT libff::g1_curve_point_at_x | ( | const typename GroupT::base_field & | x | ) |
◆ g2_curve_point_at_x()
| GroupT libff::g2_curve_point_at_x | ( | const typename GroupT::twist_field & | x | ) |
◆ get_exp_window_size()
| size_t libff::get_exp_window_size | ( | const size_t | num_scalars | ) |
Compute window size for the given number of scalars.
◆ get_nsec_cpu_time()
| long long libff::get_nsec_cpu_time | ( | ) |
◆ get_nsec_time()
| long long libff::get_nsec_time | ( | ) |
◆ get_power_of_two()
| size_t libff::get_power_of_two | ( | size_t | n | ) |
◆ get_root_of_unity() [1/2]
| std::enable_if<std::is_same<FieldT, Double>::value, FieldT>::type libff::get_root_of_unity | ( | const size_t | n | ) |
◆ get_root_of_unity() [2/2]
| std::enable_if<!std::is_same<FieldT, Double>::value, FieldT>::type libff::get_root_of_unity | ( | const size_t | n | ) |
◆ get_window_table()
| window_table<T> libff::get_window_table | ( | const size_t | scalar_size, |
| const size_t | window, | ||
| const T & | g | ||
| ) |
Compute table of window sizes.
◆ group_read()
| void libff::group_read | ( | GroupT & | v, |
| std::istream & | in_s | ||
| ) |
◆ group_write()
| void libff::group_write | ( | const GroupT & | v, |
| std::ostream & | out_s | ||
| ) |
◆ has_root_of_unity() [1/2]
| std::enable_if<std::is_same<FieldT, Double>::value, bool>::type libff::has_root_of_unity | ( | const size_t | n | ) |
◆ has_root_of_unity() [2/2]
| std::enable_if<!std::is_same<FieldT, Double>::value, bool>::type libff::has_root_of_unity | ( | const size_t | n | ) |
◆ hex_to_bytes_reversed()
| void libff::hex_to_bytes_reversed | ( | const std::string & | hex, |
| void * | dest, | ||
| size_t | bytes | ||
| ) |
Definition at line 72 of file serialization.cpp.
◆ init_alt_bn128_params()
| void libff::init_alt_bn128_params | ( | ) |
Definition at line 32 of file alt_bn128_init.cpp.
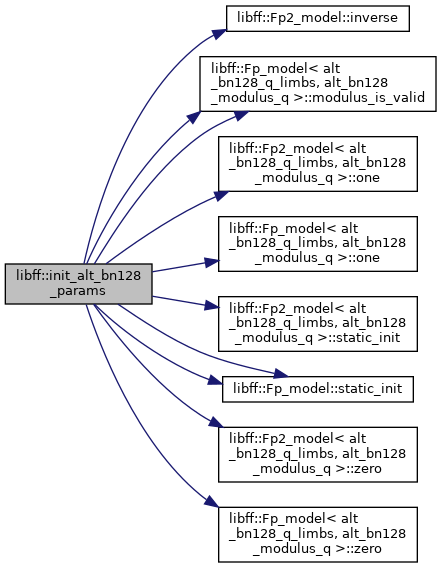

◆ init_bls12_377_params()
| void libff::init_bls12_377_params | ( | ) |
Definition at line 50 of file bls12_377_init.cpp.
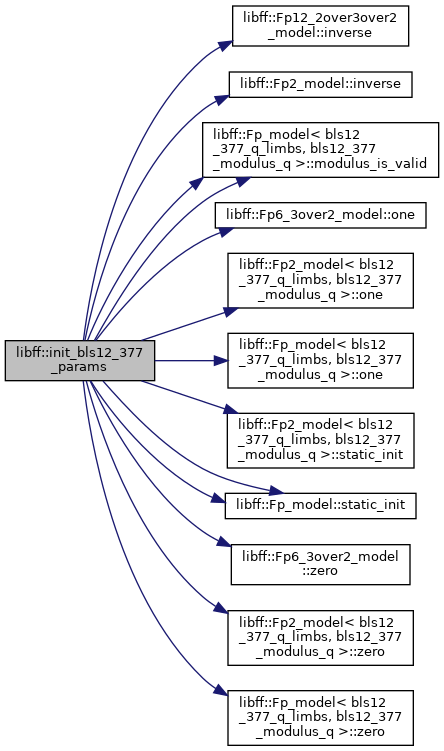

◆ init_bls12_381_params()
| void libff::init_bls12_381_params | ( | ) |
Definition at line 26 of file bls12_381_init.cpp.
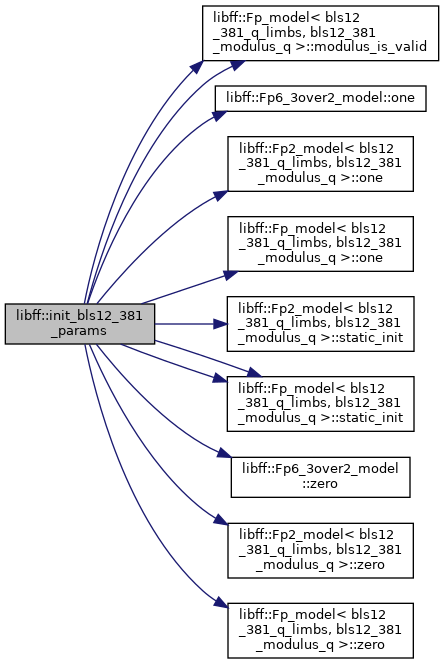

◆ init_bn128_params()
| void libff::init_bn128_params | ( | ) |
Definition at line 29 of file bn128_init.cpp.
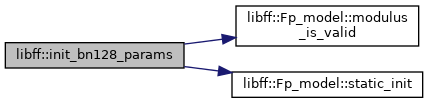

◆ init_bw6_761_params()
| void libff::init_bw6_761_params | ( | ) |
Definition at line 27 of file bw6_761_init.cpp.

◆ init_edwards_params()
| void libff::init_edwards_params | ( | ) |
Definition at line 38 of file edwards_init.cpp.

◆ init_mnt4_params()
| void libff::init_mnt4_params | ( | ) |
Definition at line 41 of file mnt4_init.cpp.

◆ init_mnt6_params()
| void libff::init_mnt6_params | ( | ) |
Definition at line 43 of file mnt6_init.cpp.

◆ inner_product()
| T libff::inner_product | ( | typename std::vector< T >::const_iterator | a_start, |
| typename std::vector< T >::const_iterator | a_end, | ||
| typename std::vector< T >::const_iterator | b_start, | ||
| typename std::vector< T >::const_iterator | b_end | ||
| ) |
A convenience function for calculating a pure inner product, where the more complicated methods are not required.
◆ input_bool()
|
inline |
◆ input_bool_vector()
|
inline |
◆ int_list_to_bits()
| bit_vector libff::int_list_to_bits | ( | const std::initializer_list< unsigned long > & | l, |
| const size_t | wordsize | ||
| ) |
◆ is_little_endian()
| bool libff::is_little_endian | ( | ) |
◆ leave_block()
| void libff::leave_block | ( | const std::string & | msg, |
| const bool | indent | ||
| ) |
◆ log2()
| size_t libff::log2 | ( | size_t | n | ) |
◆ mixed_addition_step_for_flipped_miller_loop() [1/4]
| void libff::mixed_addition_step_for_flipped_miller_loop | ( | const alt_bn128_G2 | base, |
| alt_bn128_G2 & | current, | ||
| alt_bn128_ate_ell_coeffs & | c | ||
| ) |
Definition at line 290 of file alt_bn128_pairing.cpp.

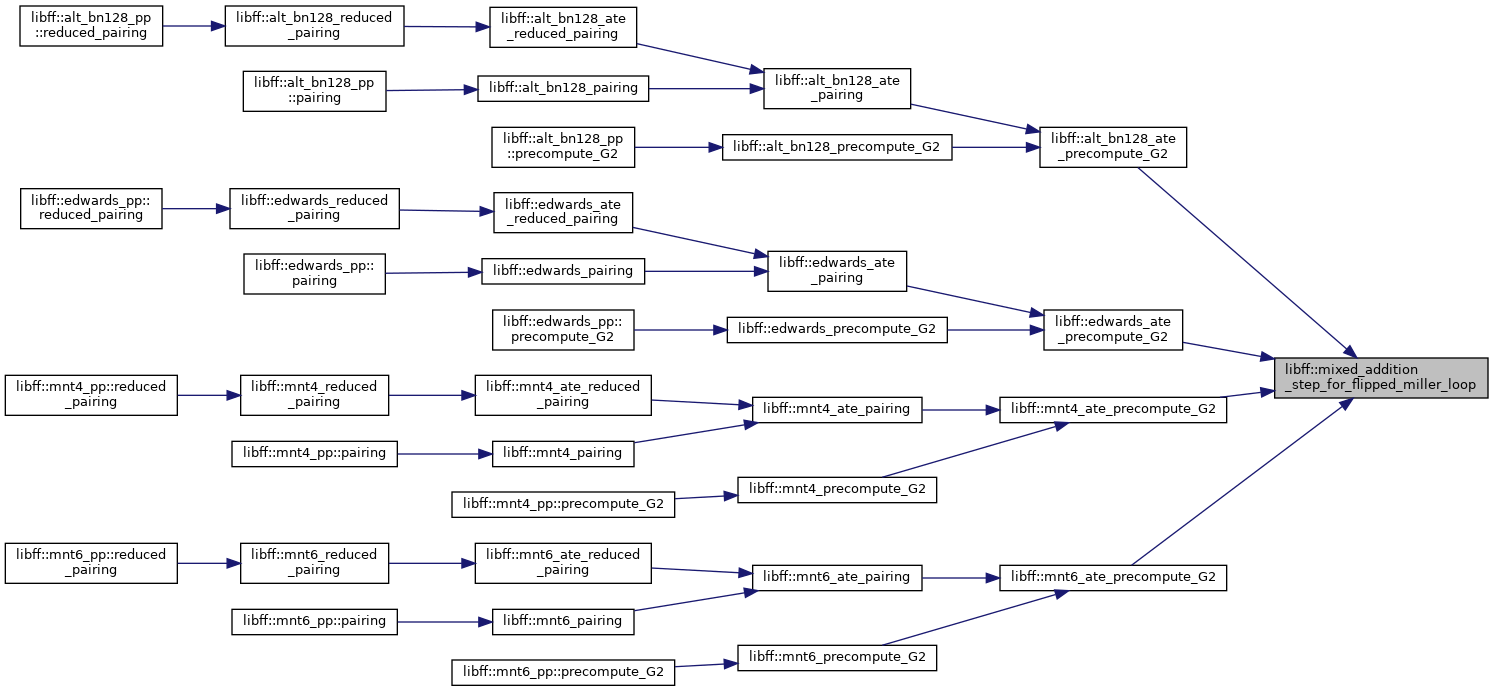
◆ mixed_addition_step_for_flipped_miller_loop() [2/4]
| void libff::mixed_addition_step_for_flipped_miller_loop | ( | const extended_edwards_G2_projective & | base, |
| extended_edwards_G2_projective & | current, | ||
| edwards_Fq3_conic_coefficients & | cc | ||
| ) |
◆ mixed_addition_step_for_flipped_miller_loop() [3/4]
| void libff::mixed_addition_step_for_flipped_miller_loop | ( | const mnt4_Fq2 | base_X, |
| const mnt4_Fq2 | base_Y, | ||
| const mnt4_Fq2 | base_Y_squared, | ||
| extended_mnt4_G2_projective & | current, | ||
| mnt4_ate_add_coeffs & | ac | ||
| ) |
◆ mixed_addition_step_for_flipped_miller_loop() [4/4]
| void libff::mixed_addition_step_for_flipped_miller_loop | ( | const mnt6_Fq3 | base_X, |
| const mnt6_Fq3 | base_Y, | ||
| const mnt6_Fq3 | base_Y_squared, | ||
| extended_mnt6_G2_projective & | current, | ||
| mnt6_ate_add_coeffs & | ac | ||
| ) |
◆ mixed_addition_step_for_miller_loop() [1/2]
| void libff::mixed_addition_step_for_miller_loop | ( | const bw6_761_G2 | base, |
| bw6_761_G2 & | current, | ||
| bw6_761_ate_ell_coeffs & | c | ||
| ) |
Definition at line 319 of file bw6_761_pairing.cpp.


◆ mixed_addition_step_for_miller_loop() [2/2]
| void libff::mixed_addition_step_for_miller_loop | ( | const extended_edwards_G1_projective & | base, |
| extended_edwards_G1_projective & | current, | ||
| edwards_Fq_conic_coefficients & | cc | ||
| ) |
◆ mnt4_affine_ate_miller_loop()
| mnt4_Fq4 libff::mnt4_affine_ate_miller_loop | ( | const mnt4_affine_ate_G1_precomputation & | prec_P, |
| const mnt4_affine_ate_G2_precomputation & | prec_Q | ||
| ) |
Definition at line 318 of file mnt4_pairing.cpp.
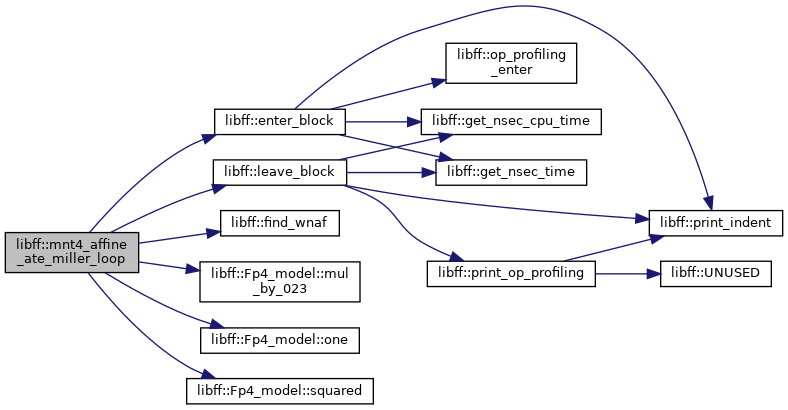
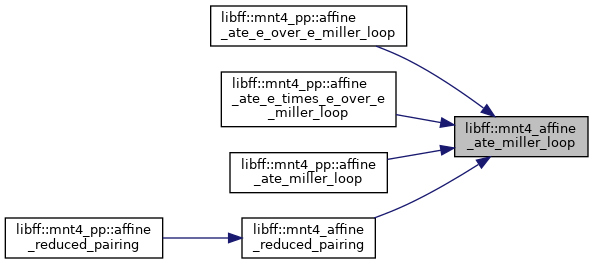
◆ mnt4_affine_ate_precompute_G1()
| mnt4_affine_ate_G1_precomputation libff::mnt4_affine_ate_precompute_G1 | ( | const mnt4_G1 & | P | ) |
Definition at line 224 of file mnt4_pairing.cpp.
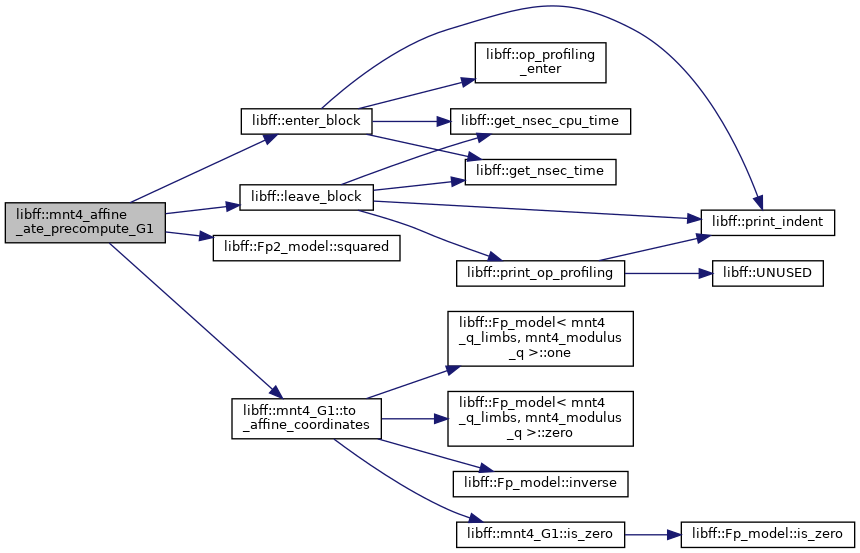

◆ mnt4_affine_ate_precompute_G2()
| mnt4_affine_ate_G2_precomputation libff::mnt4_affine_ate_precompute_G2 | ( | const mnt4_G2 & | Q | ) |
Definition at line 241 of file mnt4_pairing.cpp.
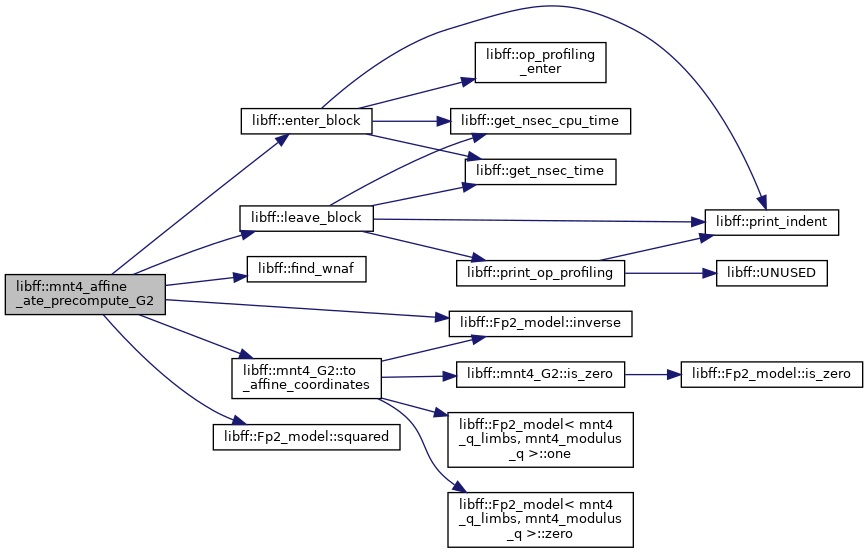

◆ mnt4_affine_reduced_pairing()
Definition at line 730 of file mnt4_pairing.cpp.
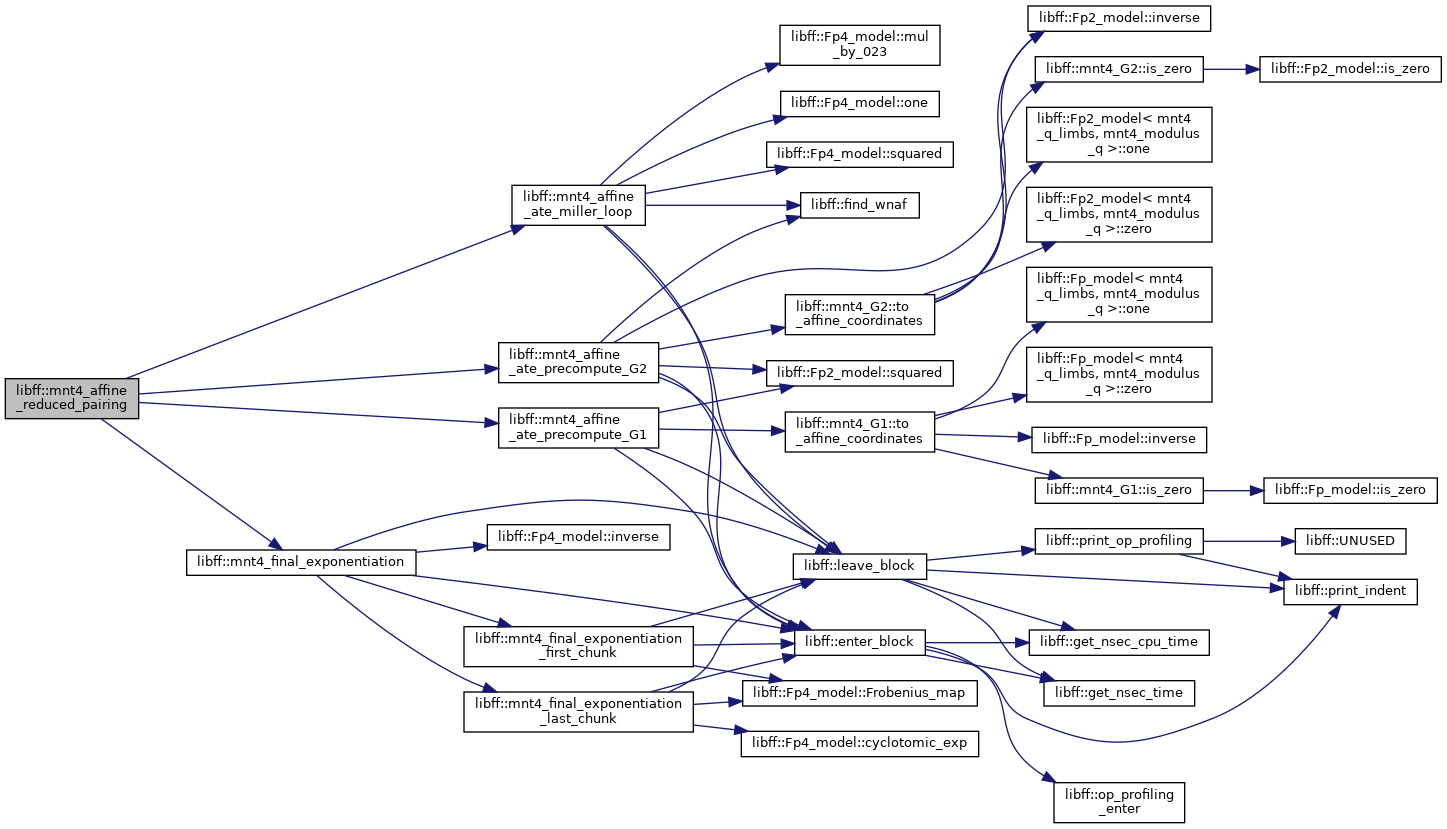

◆ mnt4_ate_double_miller_loop()
| mnt4_Fq4 libff::mnt4_ate_double_miller_loop | ( | const mnt4_ate_G1_precomp & | prec_P1, |
| const mnt4_ate_G2_precomp & | prec_Q1, | ||
| const mnt4_ate_G1_precomp & | prec_P2, | ||
| const mnt4_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 595 of file mnt4_pairing.cpp.
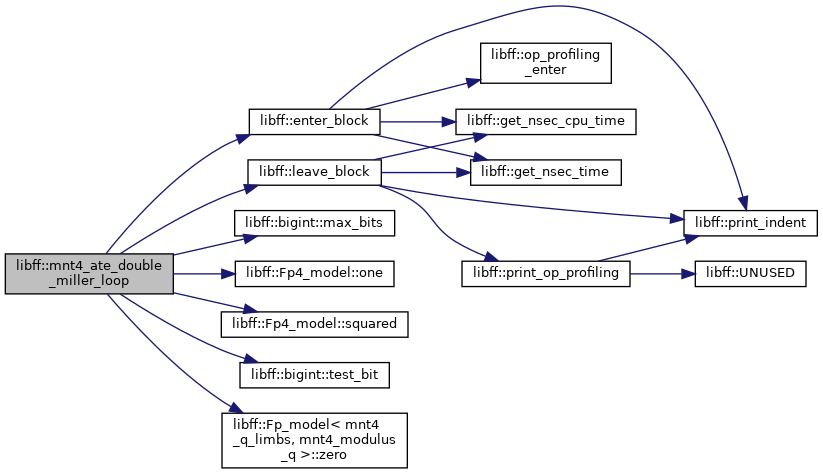

◆ mnt4_ate_miller_loop()
| mnt4_Fq4 libff::mnt4_ate_miller_loop | ( | const mnt4_ate_G1_precomp & | prec_P, |
| const mnt4_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 539 of file mnt4_pairing.cpp.
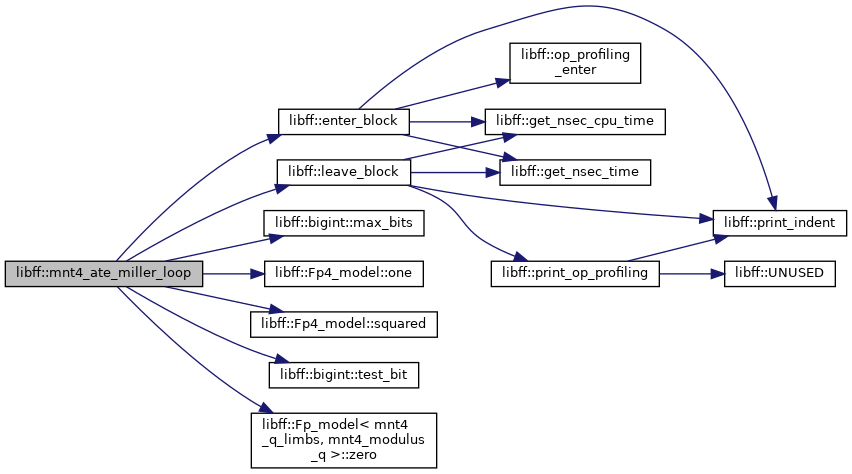

◆ mnt4_ate_pairing()
Definition at line 676 of file mnt4_pairing.cpp.
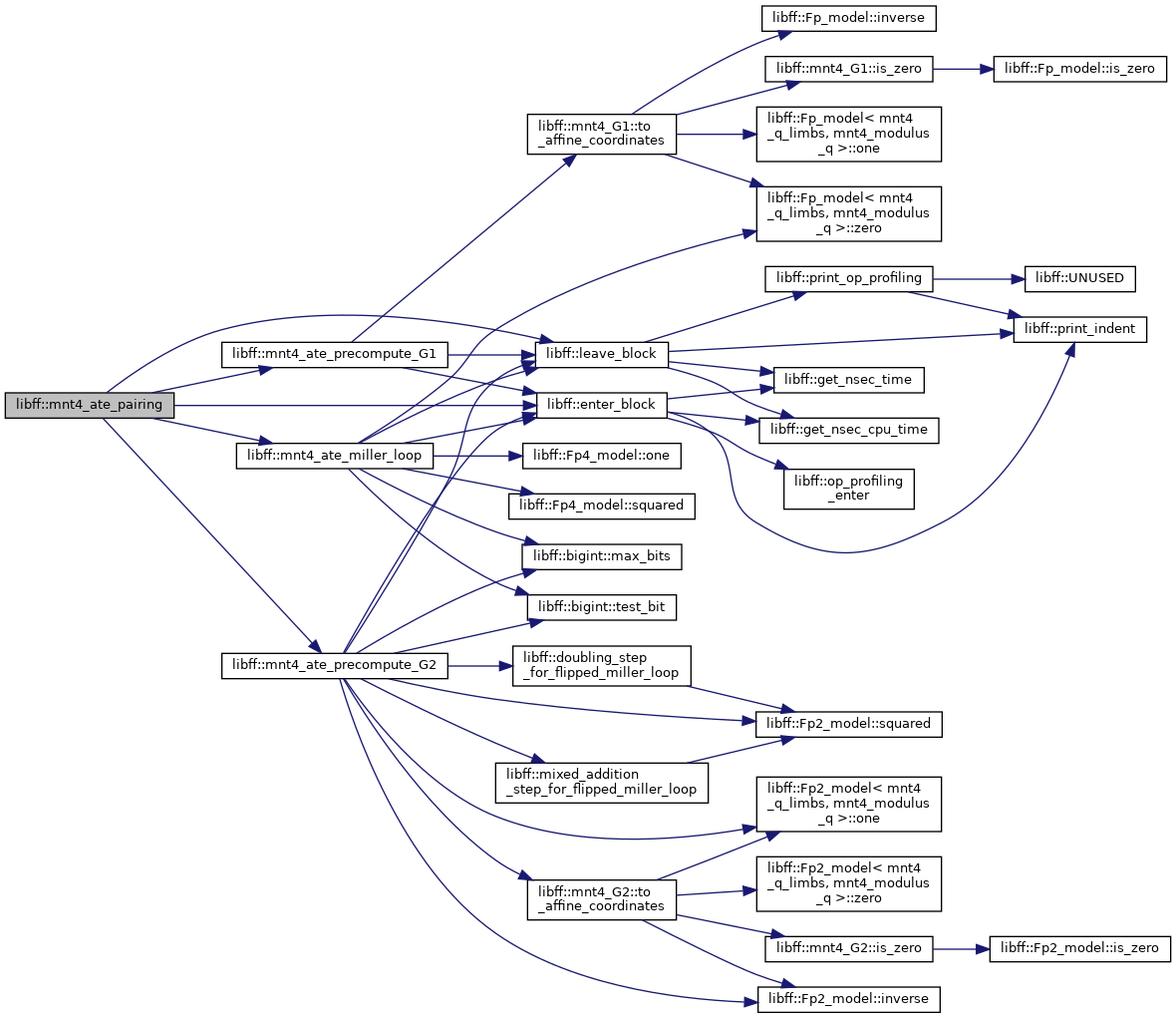

◆ mnt4_ate_precompute_G1()
| mnt4_ate_G1_precomp libff::mnt4_ate_precompute_G1 | ( | const mnt4_G1 & | P | ) |
Definition at line 463 of file mnt4_pairing.cpp.
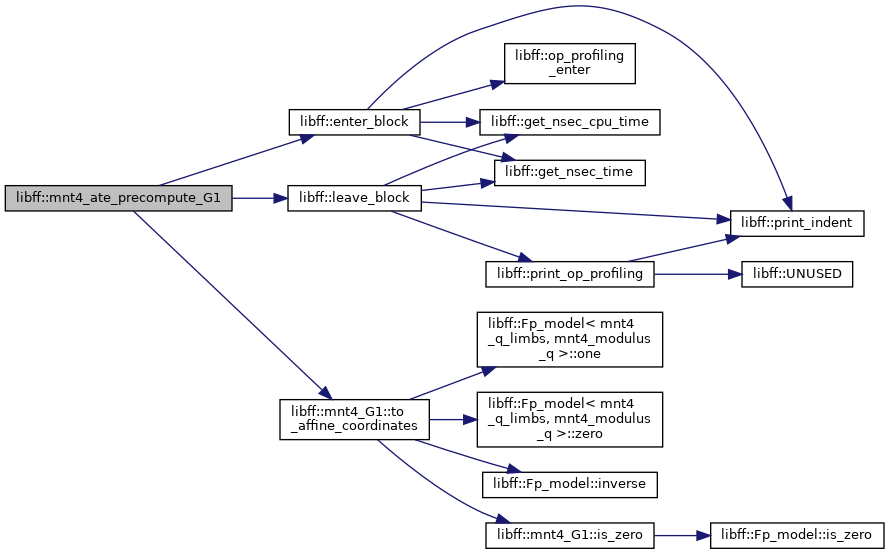

◆ mnt4_ate_precompute_G2()
| mnt4_ate_G2_precomp libff::mnt4_ate_precompute_G2 | ( | const mnt4_G2 & | Q | ) |
Definition at line 480 of file mnt4_pairing.cpp.
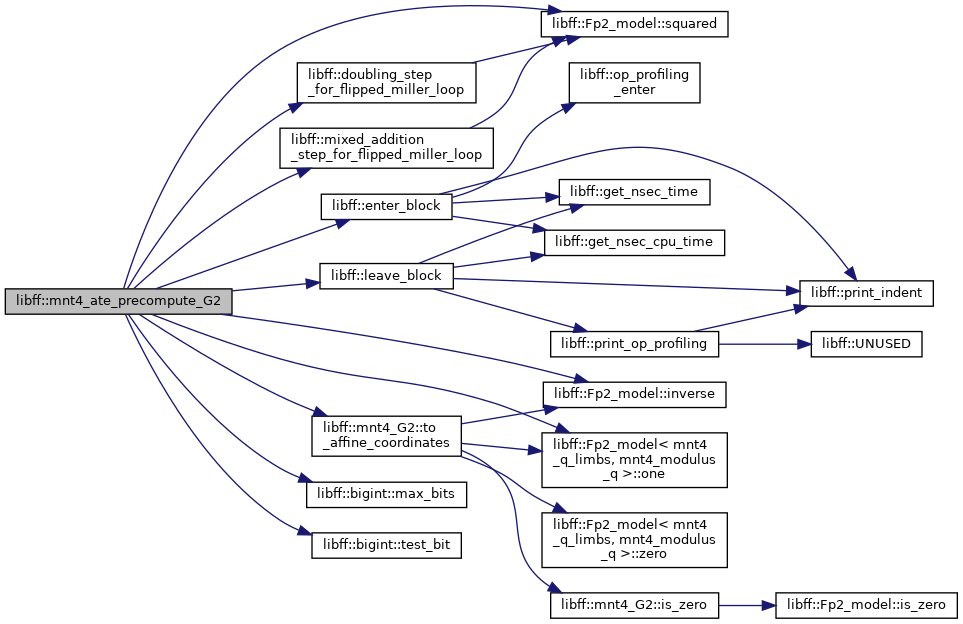

◆ mnt4_ate_reduced_pairing()
Definition at line 686 of file mnt4_pairing.cpp.
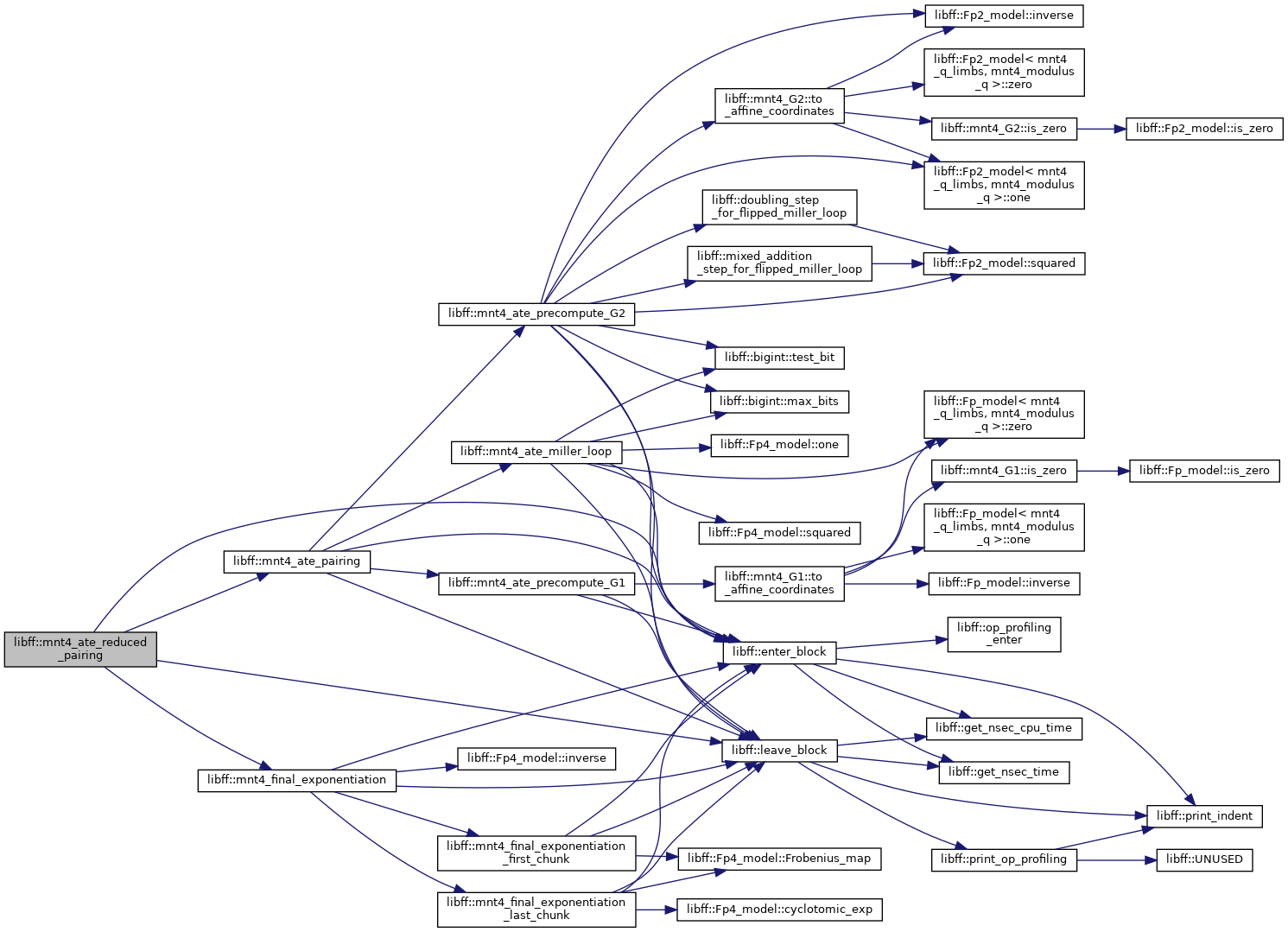

◆ mnt4_double_miller_loop()
| mnt4_Fq4 libff::mnt4_double_miller_loop | ( | const mnt4_G1_precomp & | prec_P1, |
| const mnt4_G2_precomp & | prec_Q1, | ||
| const mnt4_G1_precomp & | prec_P2, | ||
| const mnt4_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 711 of file mnt4_pairing.cpp.
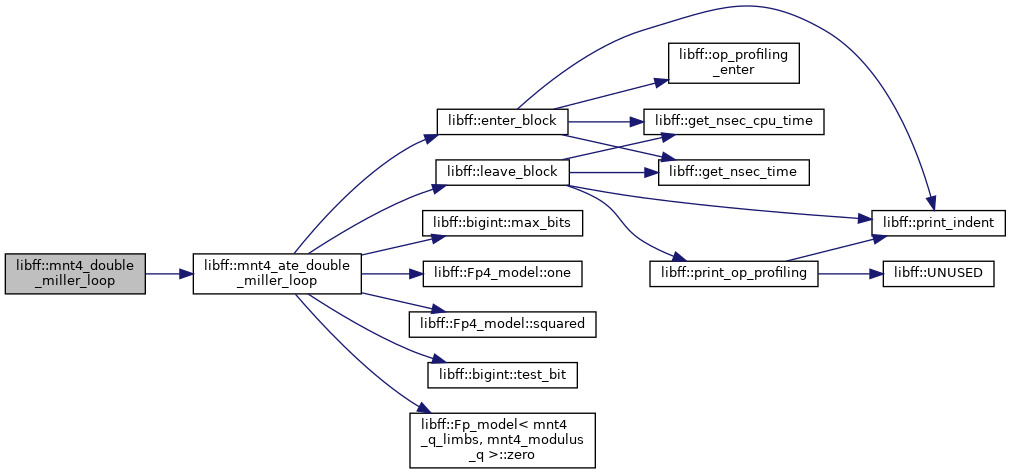

◆ mnt4_final_exponentiation()
Definition at line 207 of file mnt4_pairing.cpp.
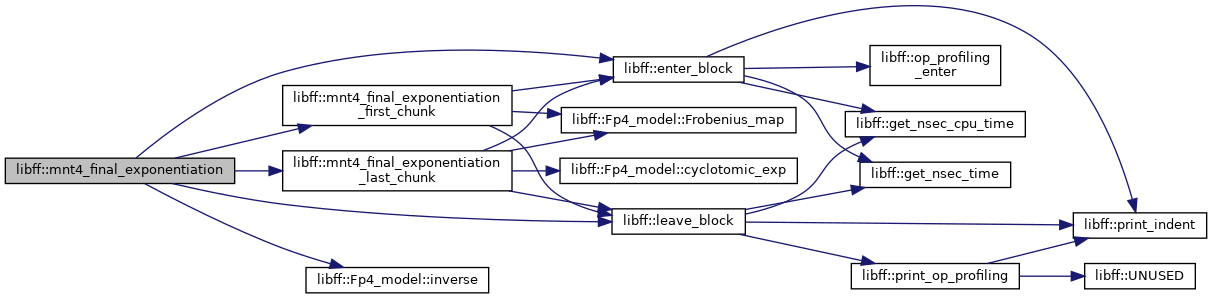
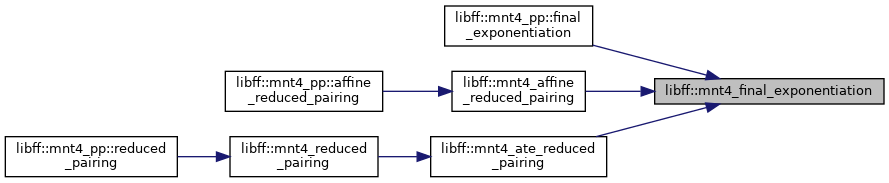
◆ mnt4_final_exponentiation_first_chunk()
| mnt4_Fq4 libff::mnt4_final_exponentiation_first_chunk | ( | const mnt4_Fq4 & | elt, |
| const mnt4_Fq4 & | elt_inv | ||
| ) |
Definition at line 191 of file mnt4_pairing.cpp.
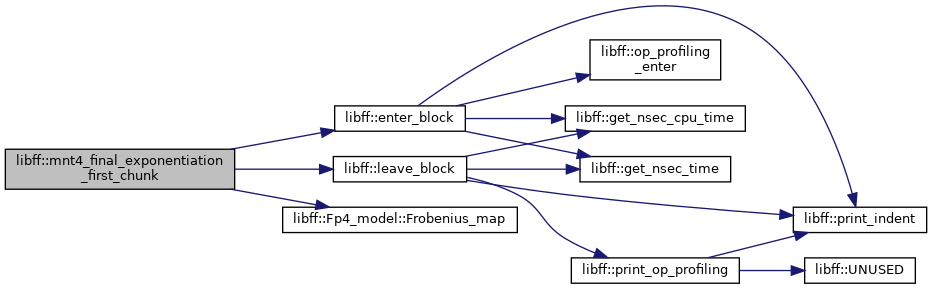

◆ mnt4_final_exponentiation_last_chunk()
| mnt4_Fq4 libff::mnt4_final_exponentiation_last_chunk | ( | const mnt4_Fq4 & | elt, |
| const mnt4_Fq4 & | elt_inv | ||
| ) |
Definition at line 172 of file mnt4_pairing.cpp.
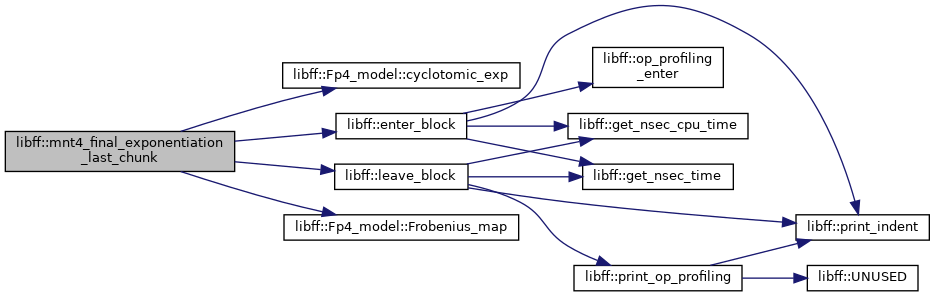

◆ mnt4_miller_loop()
| mnt4_Fq4 libff::mnt4_miller_loop | ( | const mnt4_G1_precomp & | prec_P, |
| const mnt4_G2_precomp & | prec_Q | ||
| ) |
Definition at line 705 of file mnt4_pairing.cpp.
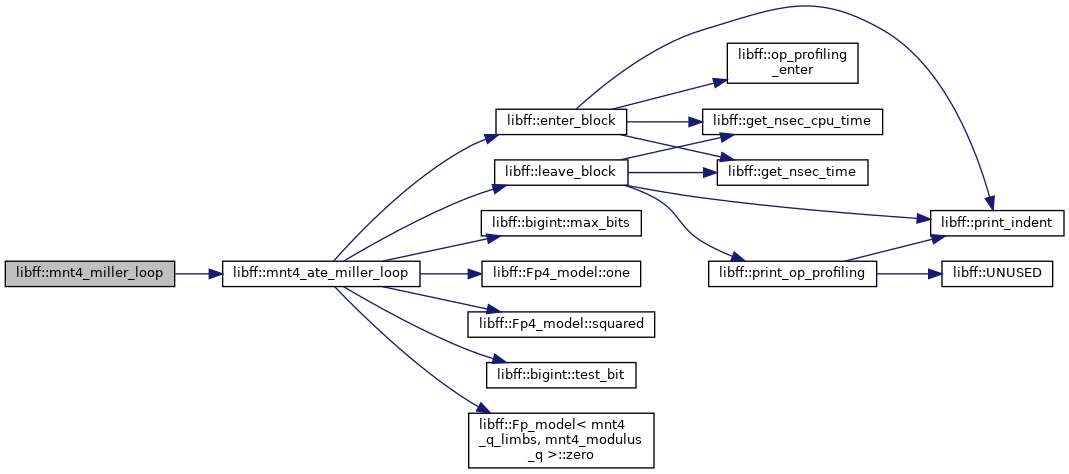

◆ mnt4_pairing()
Definition at line 720 of file mnt4_pairing.cpp.
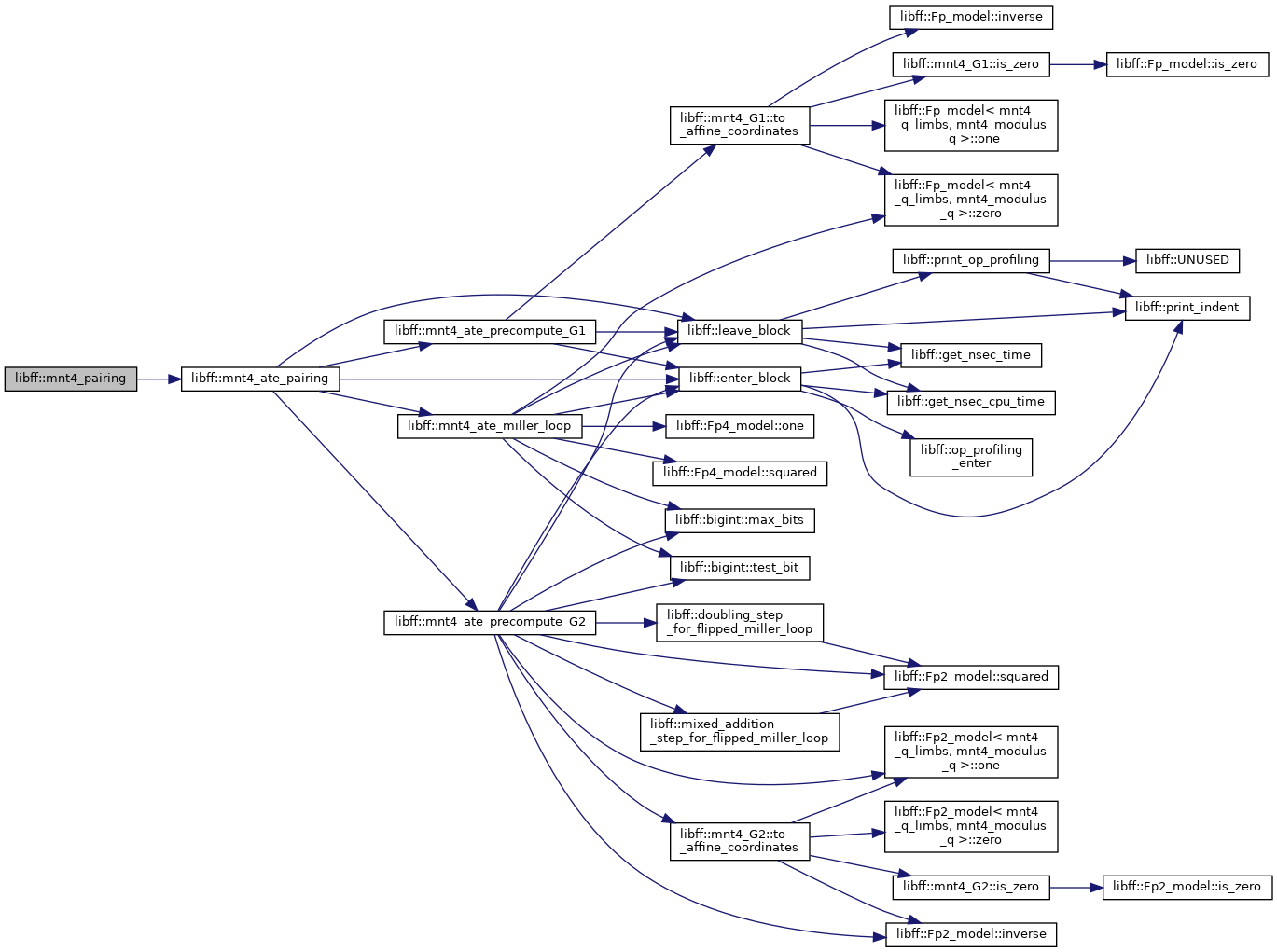

◆ mnt4_precompute_G1()
| mnt4_G1_precomp libff::mnt4_precompute_G1 | ( | const mnt4_G1 & | P | ) |
Definition at line 695 of file mnt4_pairing.cpp.
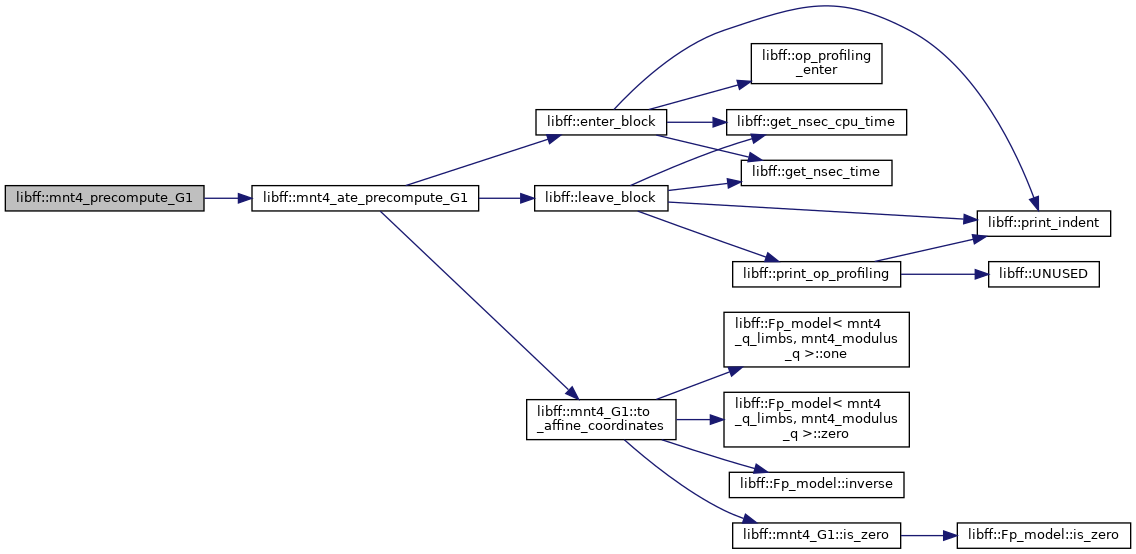

◆ mnt4_precompute_G2()
| mnt4_G2_precomp libff::mnt4_precompute_G2 | ( | const mnt4_G2 & | Q | ) |
Definition at line 700 of file mnt4_pairing.cpp.

◆ mnt4_reduced_pairing()
Definition at line 725 of file mnt4_pairing.cpp.

◆ mnt6_affine_ate_miller_loop()
| mnt6_Fq6 libff::mnt6_affine_ate_miller_loop | ( | const mnt6_affine_ate_G1_precomputation & | prec_P, |
| const mnt6_affine_ate_G2_precomputation & | prec_Q | ||
| ) |
Definition at line 323 of file mnt6_pairing.cpp.
◆ mnt6_affine_ate_precompute_G1()
| mnt6_affine_ate_G1_precomputation libff::mnt6_affine_ate_precompute_G1 | ( | const mnt6_G1 & | P | ) |
Definition at line 228 of file mnt6_pairing.cpp.
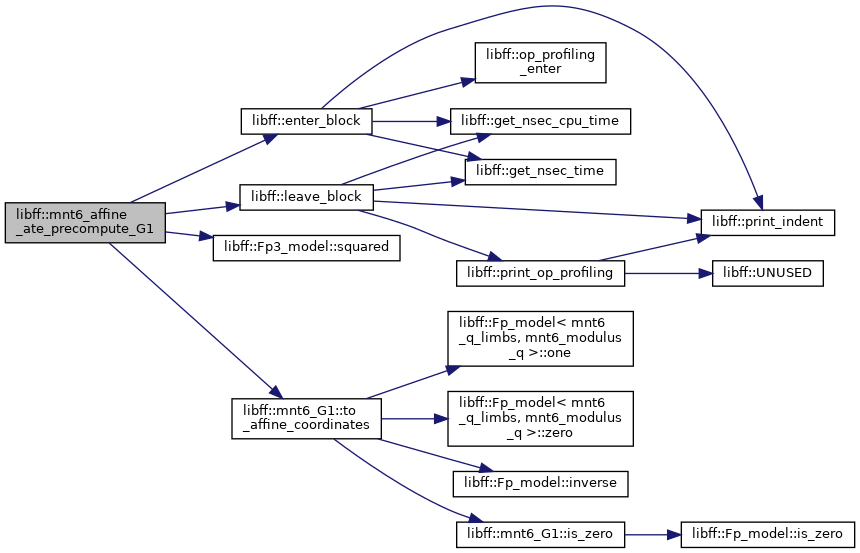

◆ mnt6_affine_ate_precompute_G2()
| mnt6_affine_ate_G2_precomputation libff::mnt6_affine_ate_precompute_G2 | ( | const mnt6_G2 & | Q | ) |
Definition at line 245 of file mnt6_pairing.cpp.
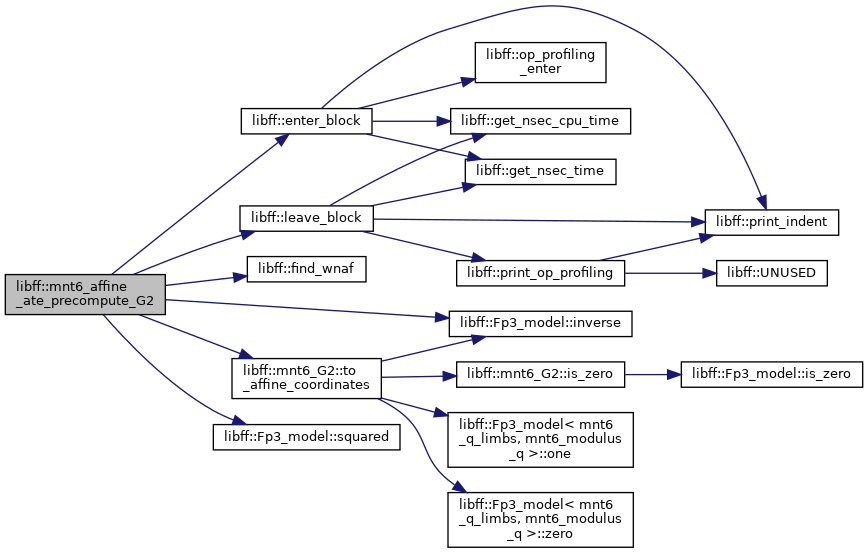

◆ mnt6_affine_reduced_pairing()
Definition at line 743 of file mnt6_pairing.cpp.
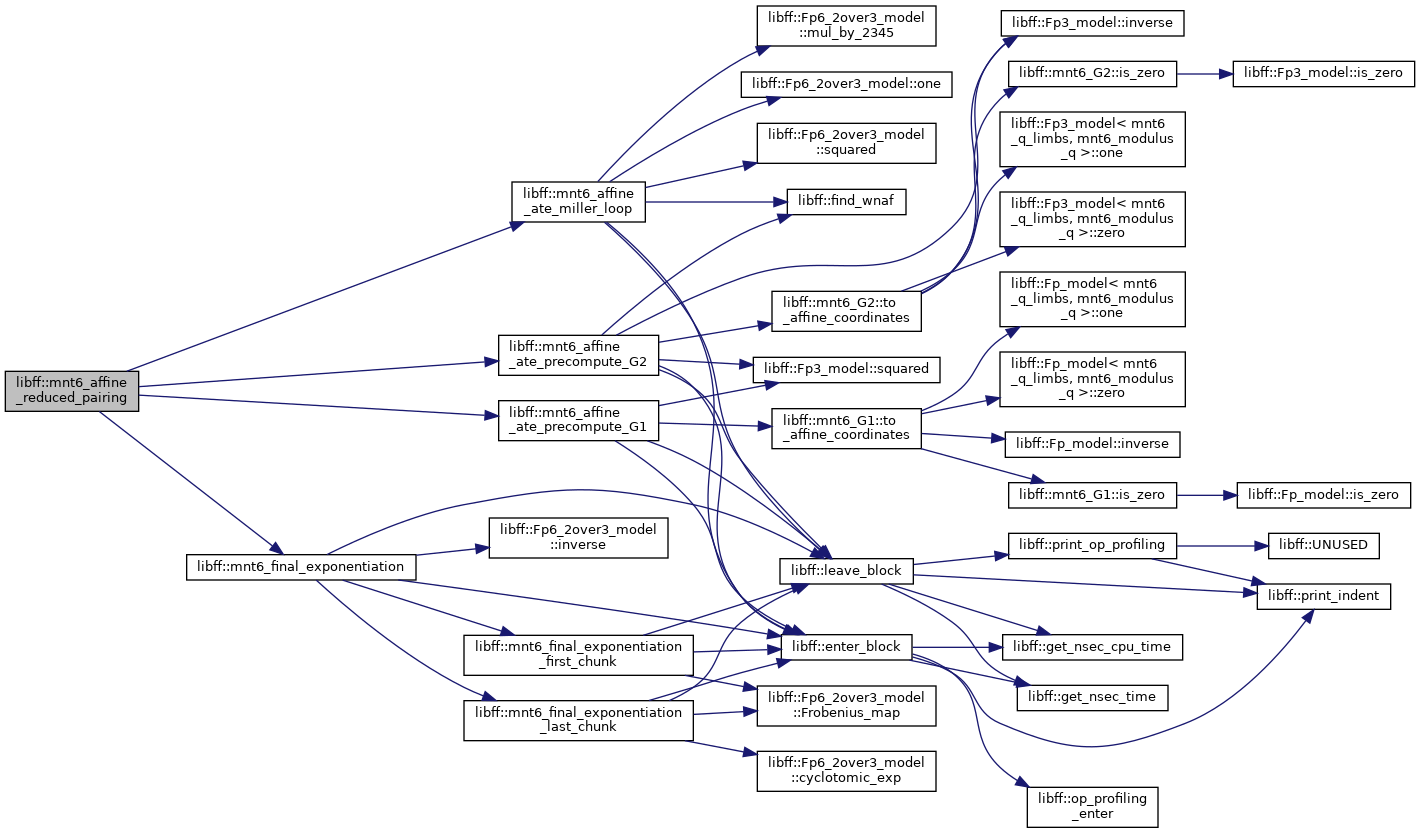

◆ mnt6_ate_double_miller_loop()
| mnt6_Fq6 libff::mnt6_ate_double_miller_loop | ( | const mnt6_ate_G1_precomp & | prec_P1, |
| const mnt6_ate_G2_precomp & | prec_Q1, | ||
| const mnt6_ate_G1_precomp & | prec_P2, | ||
| const mnt6_ate_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 605 of file mnt6_pairing.cpp.
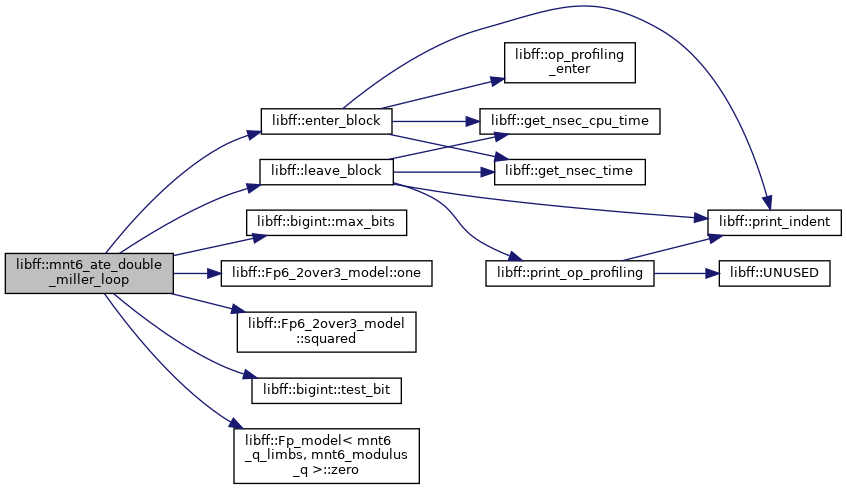

◆ mnt6_ate_miller_loop()
| mnt6_Fq6 libff::mnt6_ate_miller_loop | ( | const mnt6_ate_G1_precomp & | prec_P, |
| const mnt6_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 548 of file mnt6_pairing.cpp.
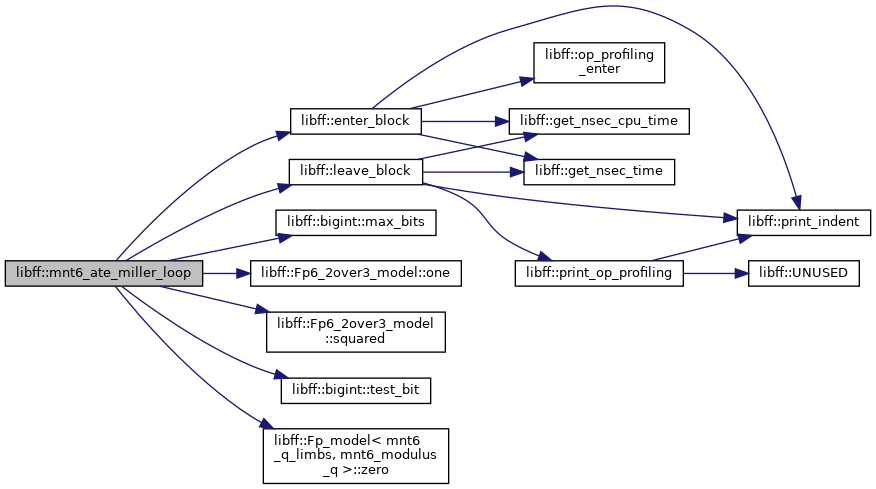

◆ mnt6_ate_pairing()
Definition at line 689 of file mnt6_pairing.cpp.
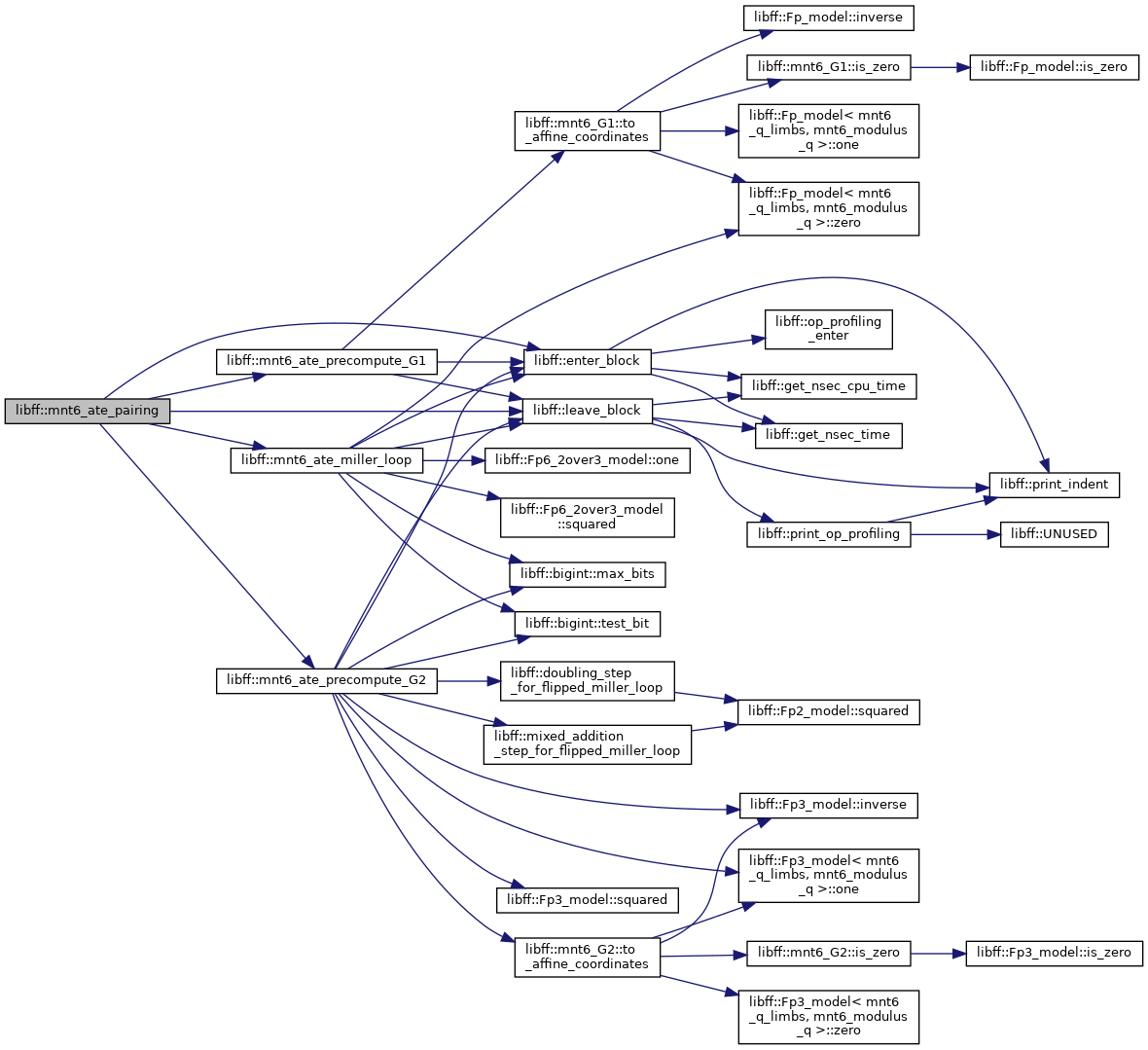

◆ mnt6_ate_precompute_G1()
| mnt6_ate_G1_precomp libff::mnt6_ate_precompute_G1 | ( | const mnt6_G1 & | P | ) |
Definition at line 468 of file mnt6_pairing.cpp.
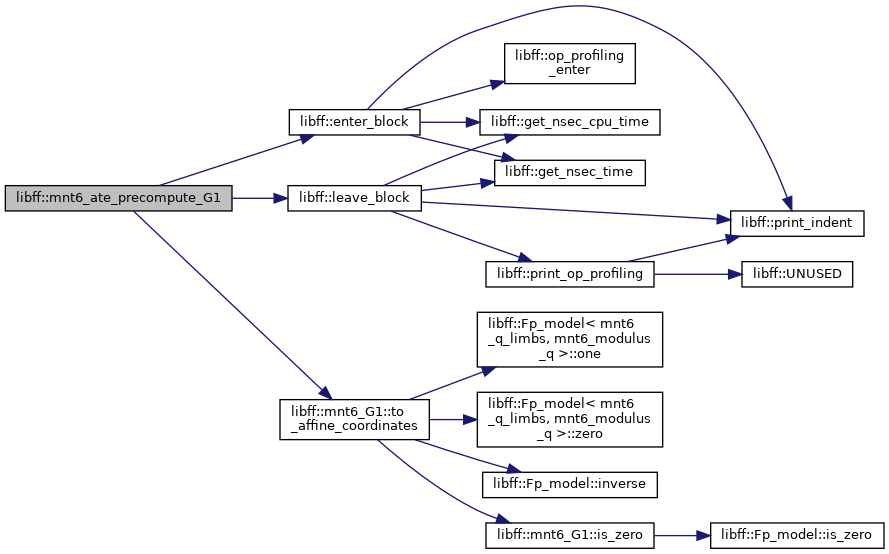

◆ mnt6_ate_precompute_G2()
| mnt6_ate_G2_precomp libff::mnt6_ate_precompute_G2 | ( | const mnt6_G2 & | Q | ) |
Definition at line 485 of file mnt6_pairing.cpp.
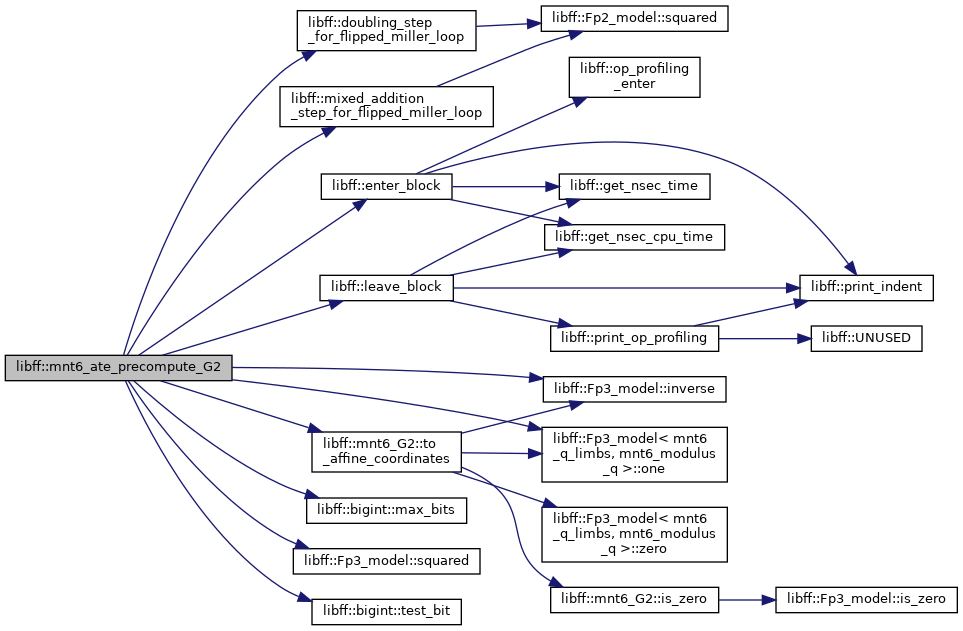

◆ mnt6_ate_reduced_pairing()
Definition at line 699 of file mnt6_pairing.cpp.
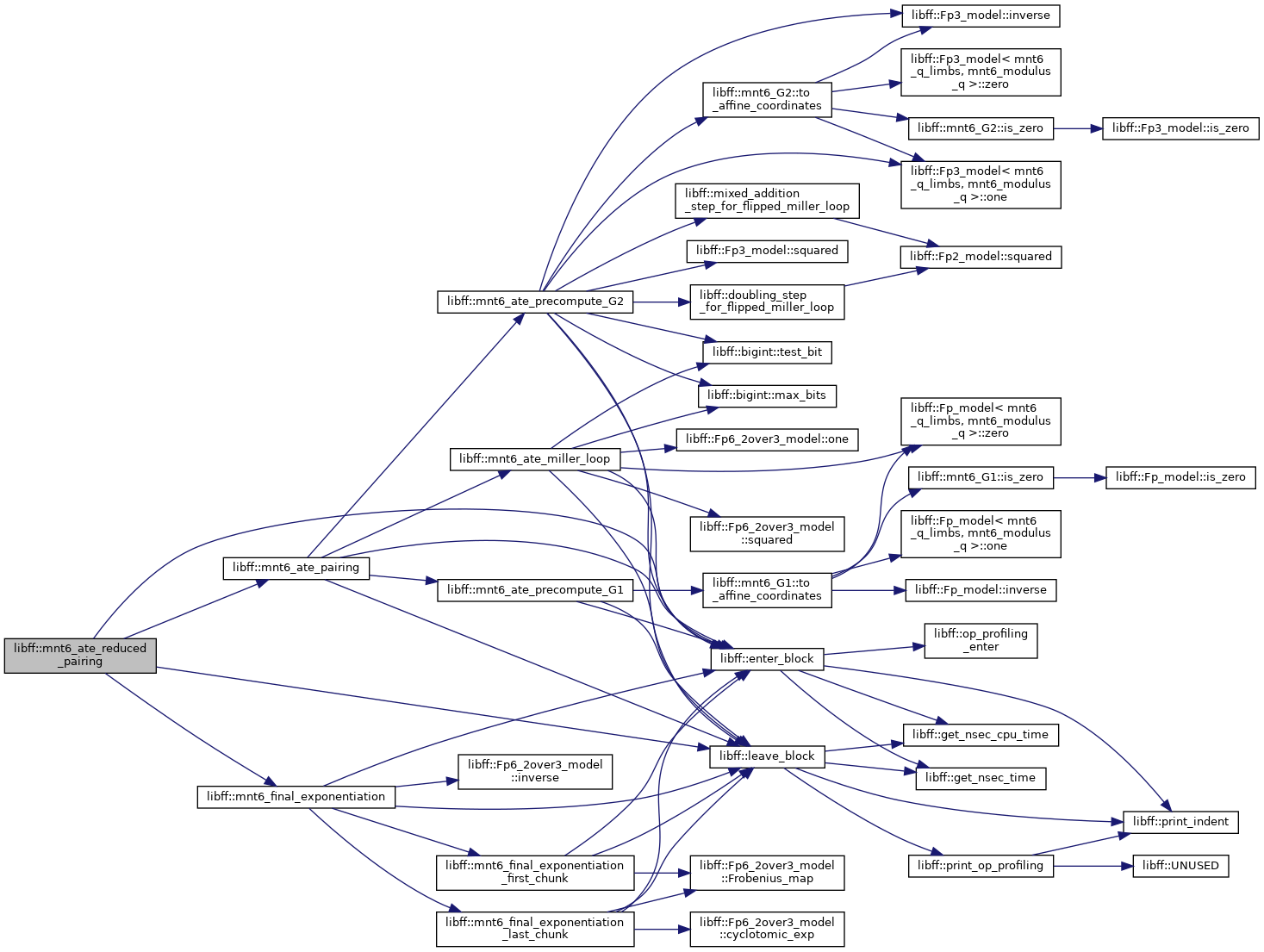

◆ mnt6_double_miller_loop()
| mnt6_Fq6 libff::mnt6_double_miller_loop | ( | const mnt6_G1_precomp & | prec_P1, |
| const mnt6_G2_precomp & | prec_Q1, | ||
| const mnt6_G1_precomp & | prec_P2, | ||
| const mnt6_G2_precomp & | prec_Q2 | ||
| ) |
Definition at line 724 of file mnt6_pairing.cpp.
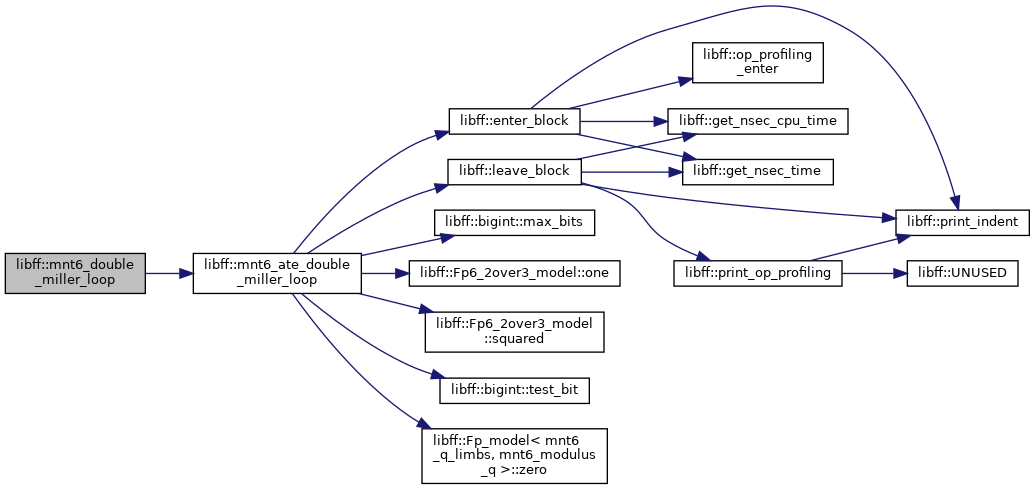

◆ mnt6_final_exponentiation()
Definition at line 211 of file mnt6_pairing.cpp.
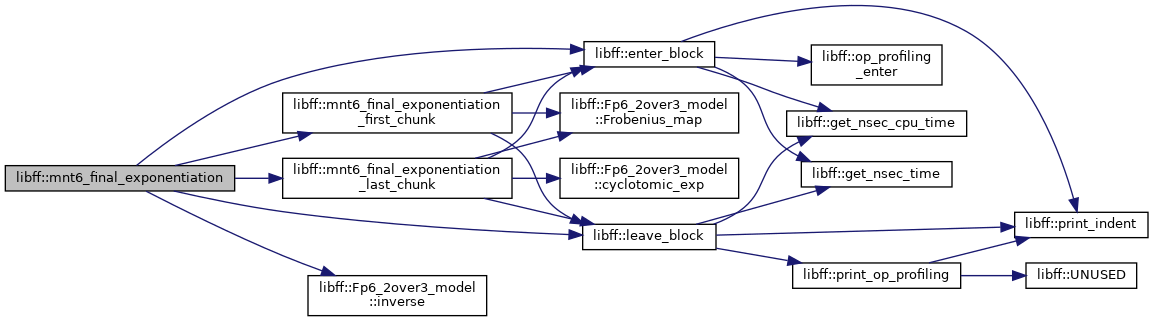
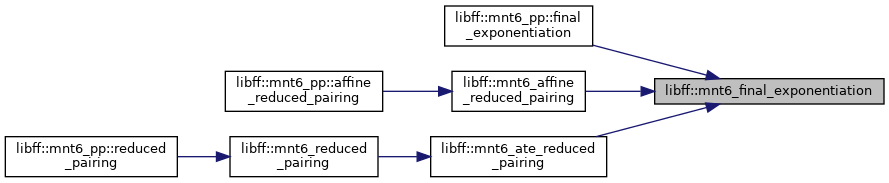
◆ mnt6_final_exponentiation_first_chunk()
| mnt6_Fq6 libff::mnt6_final_exponentiation_first_chunk | ( | const mnt6_Fq6 & | elt, |
| const mnt6_Fq6 & | elt_inv | ||
| ) |
Definition at line 192 of file mnt6_pairing.cpp.
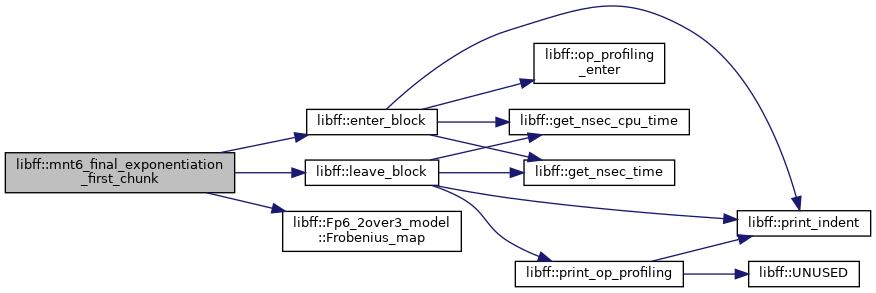

◆ mnt6_final_exponentiation_last_chunk()
| mnt6_Fq6 libff::mnt6_final_exponentiation_last_chunk | ( | const mnt6_Fq6 & | elt, |
| const mnt6_Fq6 & | elt_inv | ||
| ) |
Definition at line 173 of file mnt6_pairing.cpp.
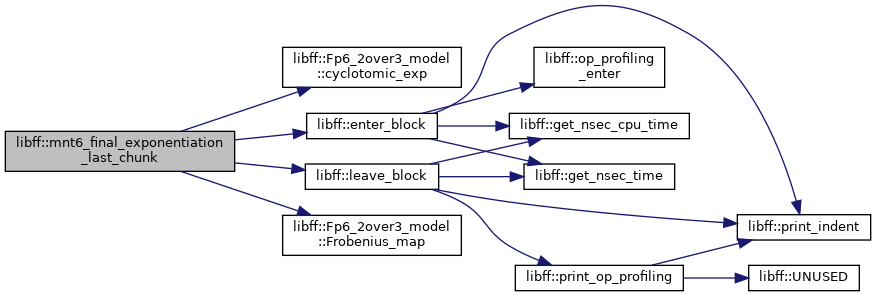

◆ mnt6_miller_loop()
| mnt6_Fq6 libff::mnt6_miller_loop | ( | const mnt6_G1_precomp & | prec_P, |
| const mnt6_G2_precomp & | prec_Q | ||
| ) |
Definition at line 718 of file mnt6_pairing.cpp.
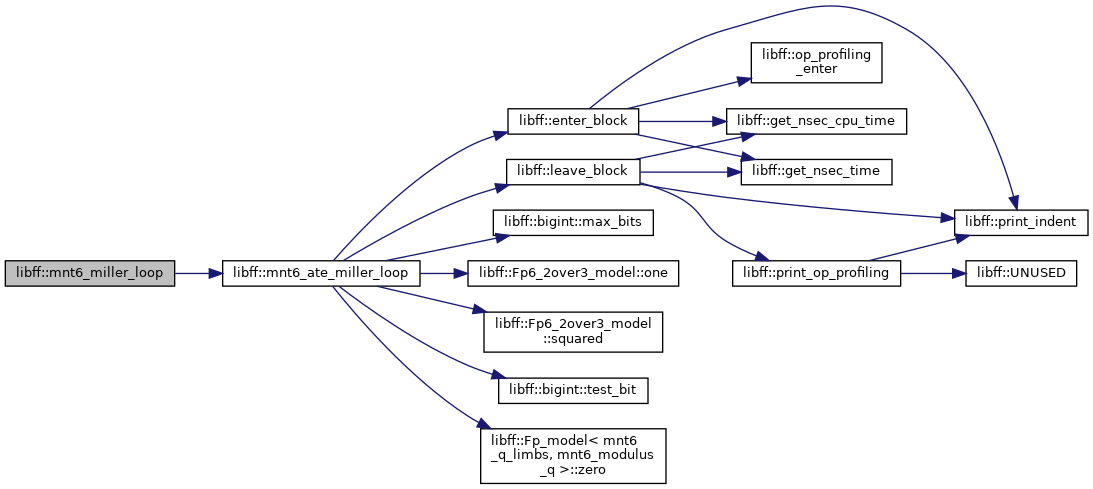

◆ mnt6_pairing()
Definition at line 733 of file mnt6_pairing.cpp.
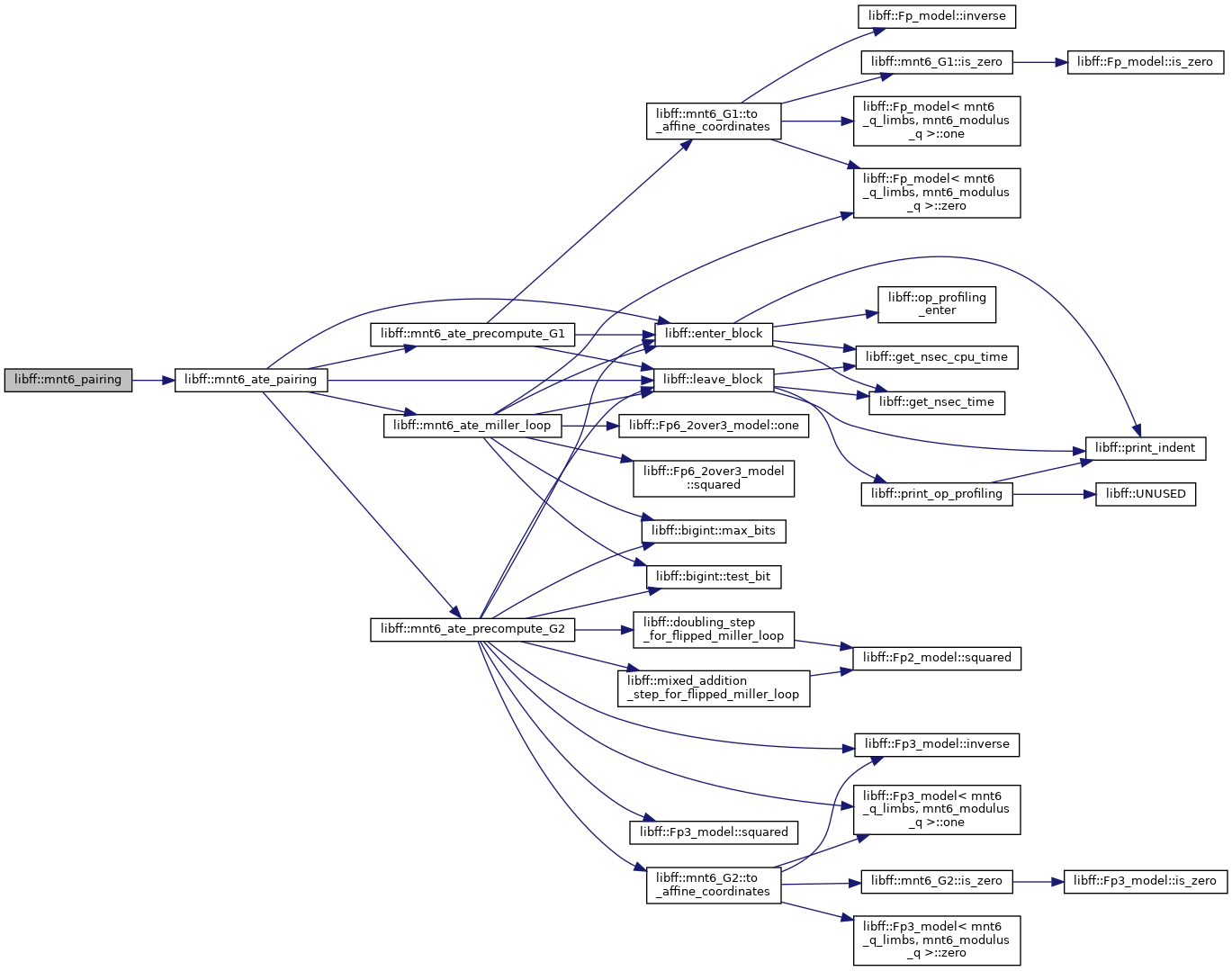

◆ mnt6_precompute_G1()
| mnt6_G1_precomp libff::mnt6_precompute_G1 | ( | const mnt6_G1 & | P | ) |
Definition at line 708 of file mnt6_pairing.cpp.
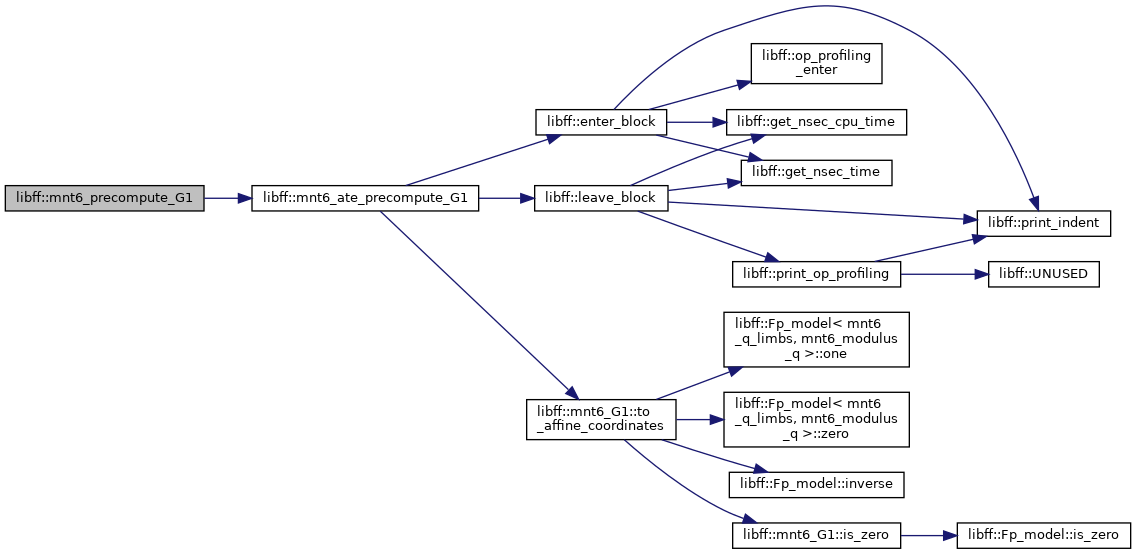

◆ mnt6_precompute_G2()
| mnt6_G2_precomp libff::mnt6_precompute_G2 | ( | const mnt6_G2 & | Q | ) |
Definition at line 713 of file mnt6_pairing.cpp.
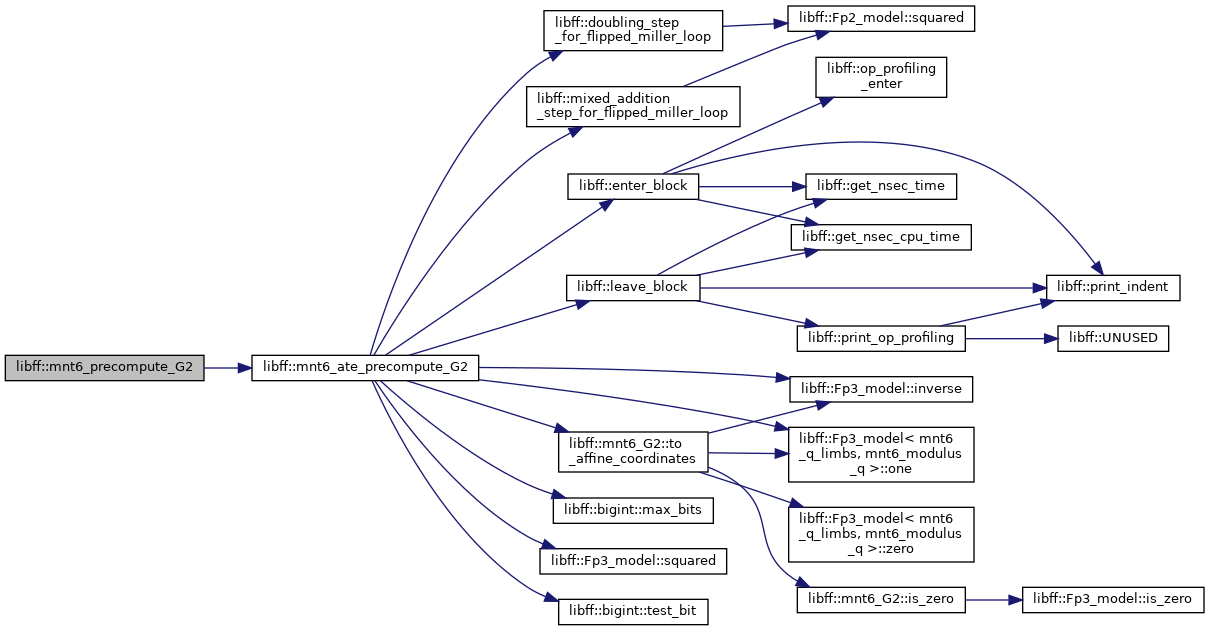

◆ mnt6_reduced_pairing()
Definition at line 738 of file mnt6_pairing.cpp.
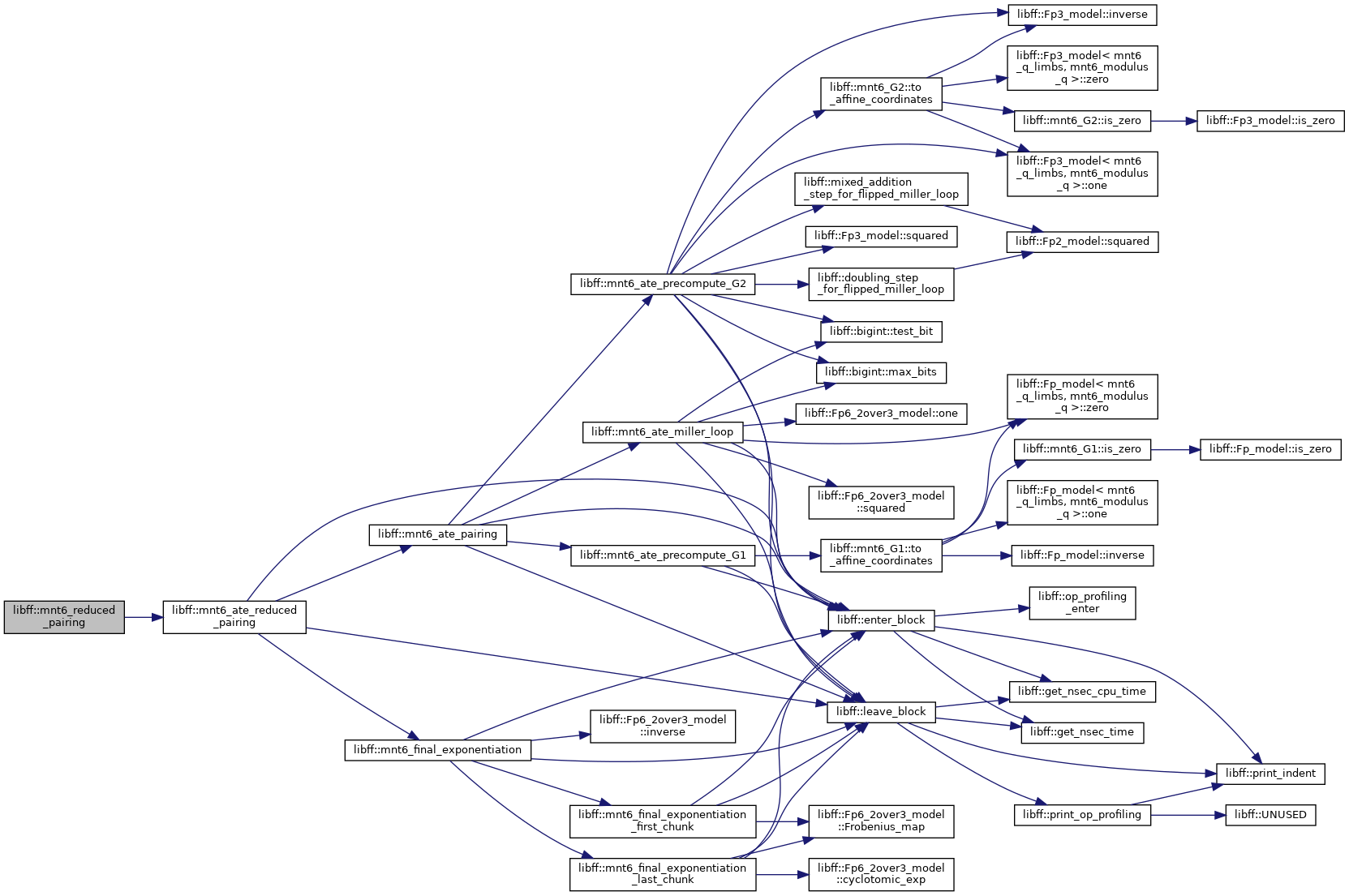

◆ multi_exp()
| T libff::multi_exp | ( | typename std::vector< T >::const_iterator | vec_start, |
| typename std::vector< T >::const_iterator | vec_end, | ||
| typename std::vector< FieldT >::const_iterator | scalar_start, | ||
| typename std::vector< FieldT >::const_iterator | scalar_end, | ||
| const size_t | chunks | ||
| ) |
Computes the sum: \sum_i scalar_start[i] * vec_start[i] using the selected method. Input is split into the given number of chunks, and processed in parallel.
◆ multi_exp_filter_one_zero()
| T libff::multi_exp_filter_one_zero | ( | typename std::vector< T >::const_iterator | vec_start, |
| typename std::vector< T >::const_iterator | vec_end, | ||
| typename std::vector< FieldT >::const_iterator | scalar_start, | ||
| typename std::vector< FieldT >::const_iterator | scalar_end, | ||
| const size_t | chunks | ||
| ) |
A variant of multi_exp which includes special pre-processing step to skip zeros, and directly sum base elements with factor 1. Remaining values are processed as usual via multi_exp.
◆ multi_exp_stream()
| GroupT libff::multi_exp_stream | ( | std::istream & | base_elements_in, |
| const std::vector< FieldT > & | exponents | ||
| ) |
Read base elements from a stream. More intermediate memory is used (offset by the fact that base elements are streamed and therefore not all memory-resident) to reduce the number of internal passes. Currently processing is single-threaded (although element streaming happens in a separate temporary thread).
◆ multi_exp_stream_with_precompute()
| GroupT libff::multi_exp_stream_with_precompute | ( | std::istream & | precomputed_elements_in, |
| const std::vector< FieldT > & | exponents, | ||
| const size_t | precompute_c | ||
| ) |
Perform optimal multiexp using precomputed elements from a stream. The stream is expected to be formatted as follows: For each original base element e_i: e_i, [2^c] e_i, [2^2c] e_i, .... [2^(b-1)c] e_i where c is the digit size (in bits) to be used in the BDLO12_signed algorithm, and b = (FieldT::num_bits + c - 1) / c is the number of digits required to fully represent a scalar value.
Optimal c can be computed with bdlo12_signed_optimal_c().
◆ op_profiling_enter()
| void libff::op_profiling_enter | ( | const std::string & | msg | ) |
◆ operator*() [1/42]
| alt_bn128_G1 libff::operator* | ( | const bigint< m > & | lhs, |
| const alt_bn128_G1 & | rhs | ||
| ) |
Definition at line 99 of file alt_bn128_g1.hpp.
◆ operator*() [2/42]
| alt_bn128_G2 libff::operator* | ( | const bigint< m > & | lhs, |
| const alt_bn128_G2 & | rhs | ||
| ) |
Definition at line 103 of file alt_bn128_g2.hpp.
◆ operator*() [3/42]
| bls12_377_G1 libff::operator* | ( | const bigint< m > & | lhs, |
| const bls12_377_G1 & | rhs | ||
| ) |
Definition at line 112 of file bls12_377_g1.hpp.
◆ operator*() [4/42]
| bls12_377_G2 libff::operator* | ( | const bigint< m > & | lhs, |
| const bls12_377_G2 & | rhs | ||
| ) |
Definition at line 104 of file bls12_377_g2.hpp.
◆ operator*() [5/42]
| bls12_381_G1 libff::operator* | ( | const bigint< m > & | lhs, |
| const bls12_381_G1 & | rhs | ||
| ) |
Definition at line 99 of file bls12_381_g1.hpp.
◆ operator*() [6/42]
| bls12_381_G2 libff::operator* | ( | const bigint< m > & | lhs, |
| const bls12_381_G2 & | rhs | ||
| ) |
Definition at line 106 of file bls12_381_g2.hpp.
◆ operator*() [7/42]
Definition at line 106 of file bn128_g1.hpp.
◆ operator*() [8/42]
Definition at line 106 of file bn128_g2.hpp.
◆ operator*() [9/42]
| bw6_761_G1 libff::operator* | ( | const bigint< m > & | lhs, |
| const bw6_761_G1 & | rhs | ||
| ) |
Definition at line 94 of file bw6_761_g1.hpp.
◆ operator*() [10/42]
| bw6_761_G2 libff::operator* | ( | const bigint< m > & | lhs, |
| const bw6_761_G2 & | rhs | ||
| ) |
Definition at line 98 of file bw6_761_g2.hpp.
◆ operator*() [11/42]
| edwards_G1 libff::operator* | ( | const bigint< m > & | lhs, |
| const edwards_G1 & | rhs | ||
| ) |
Definition at line 92 of file edwards_g1.hpp.
◆ operator*() [12/42]
| edwards_G2 libff::operator* | ( | const bigint< m > & | lhs, |
| const edwards_G2 & | rhs | ||
| ) |
Definition at line 99 of file edwards_g2.hpp.
◆ operator*() [13/42]
Definition at line 106 of file mnt4_g1.hpp.
◆ operator*() [14/42]
Definition at line 106 of file mnt4_g2.hpp.
◆ operator*() [15/42]
Definition at line 109 of file mnt6_g1.hpp.
◆ operator*() [16/42]
Definition at line 111 of file mnt6_g2.hpp.
◆ operator*() [17/42]
| Fp12_2over3over2_model<n, modulus> libff::operator* | ( | const Fp2_model< n, modulus > & | lhs, |
| const Fp12_2over3over2_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [18/42]
| Fp4_model<n, modulus> libff::operator* | ( | const Fp2_model< n, modulus > & | lhs, |
| const Fp4_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [19/42]
| Fp6_3over2_model<n, modulus> libff::operator* | ( | const Fp2_model< n, modulus > & | lhs, |
| const Fp6_3over2_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [20/42]
| Fp12_2over3over2_model<n, modulus> libff::operator* | ( | const Fp6_3over2_model< n, modulus > & | lhs, |
| const Fp12_2over3over2_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [21/42]
| alt_bn128_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const alt_bn128_G1 & | rhs | ||
| ) |
◆ operator*() [22/42]
| alt_bn128_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const alt_bn128_G2 & | rhs | ||
| ) |
◆ operator*() [23/42]
| bls12_377_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bls12_377_G1 & | rhs | ||
| ) |
◆ operator*() [24/42]
| bls12_377_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bls12_377_G2 & | rhs | ||
| ) |
◆ operator*() [25/42]
| bls12_381_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bls12_381_G1 & | rhs | ||
| ) |
◆ operator*() [26/42]
| bls12_381_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bls12_381_G2 & | rhs | ||
| ) |
◆ operator*() [27/42]
| bn128_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bn128_G1 & | rhs | ||
| ) |
◆ operator*() [28/42]
| bn128_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bn128_G2 & | rhs | ||
| ) |
◆ operator*() [29/42]
| bw6_761_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bw6_761_G1 & | rhs | ||
| ) |
◆ operator*() [30/42]
| bw6_761_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const bw6_761_G2 & | rhs | ||
| ) |
◆ operator*() [31/42]
| edwards_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const edwards_G1 & | rhs | ||
| ) |
◆ operator*() [32/42]
| edwards_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const edwards_G2 & | rhs | ||
| ) |
◆ operator*() [33/42]
| mnt4_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const mnt4_G1 & | rhs | ||
| ) |
◆ operator*() [34/42]
| mnt4_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const mnt4_G2 & | rhs | ||
| ) |
◆ operator*() [35/42]
| mnt6_G1 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const mnt6_G1 & | rhs | ||
| ) |
◆ operator*() [36/42]
| mnt6_G2 libff::operator* | ( | const Fp_model< m, modulus_p > & | lhs, |
| const mnt6_G2 & | rhs | ||
| ) |
◆ operator*() [37/42]
| Fp12_2over3over2_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp12_2over3over2_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [38/42]
| Fp2_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp2_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [39/42]
| Fp3_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp3_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [40/42]
| Fp4_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp4_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [41/42]
| Fp6_2over3_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp6_2over3_model< n, modulus > & | rhs | ||
| ) |
◆ operator*() [42/42]
| Fp6_3over2_model<n, modulus> libff::operator* | ( | const Fp_model< n, modulus > & | lhs, |
| const Fp6_3over2_model< n, modulus > & | rhs | ||
| ) |
◆ operator<<() [1/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const bigint< n > & | |||
| ) |
◆ operator<<() [2/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp12_2over3over2_model< n, modulus > & | |||
| ) |
◆ operator<<() [3/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp2_model< n, modulus > & | |||
| ) |
◆ operator<<() [4/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp3_model< n, modulus > & | |||
| ) |
◆ operator<<() [5/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp4_model< n, modulus > & | |||
| ) |
◆ operator<<() [6/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp6_2over3_model< n, modulus > & | |||
| ) |
◆ operator<<() [7/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp6_3over2_model< n, modulus > & | |||
| ) |
◆ operator<<() [8/62]
| std::ostream& libff::operator<< | ( | std::ostream & | , |
| const Fp_model< n, modulus > & | |||
| ) |
◆ operator<<() [9/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const alt_bn128_ate_ell_coeffs & | c | ||
| ) |
Definition at line 49 of file alt_bn128_pairing.cpp.
◆ operator<<() [10/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const alt_bn128_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 24 of file alt_bn128_pairing.cpp.
◆ operator<<() [11/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const alt_bn128_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 75 of file alt_bn128_pairing.cpp.
◆ operator<<() [12/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const alt_bn128_G1 & | g | ||
| ) |
◆ operator<<() [13/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const alt_bn128_G2 & | g | ||
| ) |
◆ operator<<() [14/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_377_ate_ell_coeffs & | c | ||
| ) |
Definition at line 42 of file bls12_377_pairing.cpp.
◆ operator<<() [15/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_377_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 17 of file bls12_377_pairing.cpp.
◆ operator<<() [16/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_377_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 68 of file bls12_377_pairing.cpp.
◆ operator<<() [17/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bls12_377_G1 & | g | ||
| ) |
◆ operator<<() [18/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bls12_377_G2 & | g | ||
| ) |
◆ operator<<() [19/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_381_ate_ell_coeffs & | c | ||
| ) |
Definition at line 49 of file bls12_381_pairing.cpp.
◆ operator<<() [20/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_381_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 24 of file bls12_381_pairing.cpp.
◆ operator<<() [21/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bls12_381_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 75 of file bls12_381_pairing.cpp.
◆ operator<<() [22/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bls12_381_G1 & | g | ||
| ) |
◆ operator<<() [23/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bls12_381_G2 & | g | ||
| ) |
◆ operator<<() [24/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bn128_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 29 of file bn128_pairing.cpp.
◆ operator<<() [25/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bn128_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 75 of file bn128_pairing.cpp.
◆ operator<<() [26/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bn128_G1 & | g | ||
| ) |
◆ operator<<() [27/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bn128_G2 & | g | ||
| ) |
◆ operator<<() [28/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bn128_GT & | g | ||
| ) |
Definition at line 42 of file bn128_gt.cpp.
◆ operator<<() [29/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_ate_ell_coeffs & | c | ||
| ) |
Definition at line 42 of file bw6_761_pairing.cpp.
◆ operator<<() [30/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 17 of file bw6_761_pairing.cpp.
◆ operator<<() [31/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 113 of file bw6_761_pairing.cpp.
◆ operator<<() [32/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_ate_G2_precomp_iteration & | prec_Q | ||
| ) |
Definition at line 68 of file bw6_761_pairing.cpp.
◆ operator<<() [33/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_G1 & | g | ||
| ) |
◆ operator<<() [34/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const bw6_761_G2 & | g | ||
| ) |
◆ operator<<() [35/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const edwards_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 162 of file edwards_pairing.cpp.
◆ operator<<() [36/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const edwards_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 122 of file edwards_pairing.cpp.
◆ operator<<() [37/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const edwards_Fq3_conic_coefficients & | cc | ||
| ) |
Definition at line 104 of file edwards_pairing.cpp.
◆ operator<<() [38/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const edwards_Fq_conic_coefficients & | cc | ||
| ) |
Definition at line 26 of file edwards_pairing.cpp.
◆ operator<<() [39/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const edwards_G1 & | g | ||
| ) |
◆ operator<<() [40/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const edwards_G2 & | g | ||
| ) |
◆ operator<<() [41/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const edwards_tate_G1_precomp & | prec_P | ||
| ) |
Definition at line 44 of file edwards_pairing.cpp.
◆ operator<<() [42/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const edwards_tate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 81 of file edwards_pairing.cpp.
◆ operator<<() [43/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt4_ate_add_coeffs & | ac | ||
| ) |
Definition at line 85 of file mnt4_pairing.cpp.
◆ operator<<() [44/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt4_ate_dbl_coeffs & | dc | ||
| ) |
Definition at line 60 of file mnt4_pairing.cpp.
◆ operator<<() [45/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt4_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 32 of file mnt4_pairing.cpp.
◆ operator<<() [46/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt4_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 109 of file mnt4_pairing.cpp.
◆ operator<<() [47/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const mnt4_G1 & | g | ||
| ) |
◆ operator<<() [48/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const mnt4_G2 & | g | ||
| ) |
◆ operator<<() [49/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt6_ate_add_coeffs & | ac | ||
| ) |
Definition at line 85 of file mnt6_pairing.cpp.
◆ operator<<() [50/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt6_ate_dbl_coeffs & | dc | ||
| ) |
Definition at line 60 of file mnt6_pairing.cpp.
◆ operator<<() [51/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt6_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 32 of file mnt6_pairing.cpp.
◆ operator<<() [52/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const mnt6_ate_G2_precomp & | prec_Q | ||
| ) |
Definition at line 110 of file mnt6_pairing.cpp.
◆ operator<<() [53/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const mnt6_G1 & | g | ||
| ) |
◆ operator<<() [54/62]
| std::ostream & libff::operator<< | ( | std::ostream & | out, |
| const mnt6_G2 & | g | ||
| ) |
◆ operator<<() [55/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::map< T1, T2 > & | m | ||
| ) |
◆ operator<<() [56/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::set< T > & | s | ||
| ) |
◆ operator<<() [57/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< Fp12_2over3over2_model< n, modulus >> & | v | ||
| ) |
◆ operator<<() [58/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< Fp2_model< n, modulus >> & | v | ||
| ) |
◆ operator<<() [59/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< Fp3_model< n, modulus >> & | v | ||
| ) |
◆ operator<<() [60/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< Fp6_2over3_model< n, modulus >> & | v | ||
| ) |
◆ operator<<() [61/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< Fp6_3over2_model< n, modulus >> & | v | ||
| ) |
◆ operator<<() [62/62]
| std::ostream& libff::operator<< | ( | std::ostream & | out, |
| const std::vector< T > & | v | ||
| ) |
◆ operator>>() [1/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| bigint< n > & | |||
| ) |
◆ operator>>() [2/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp12_2over3over2_model< n, modulus > & | |||
| ) |
◆ operator>>() [3/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp2_model< n, modulus > & | |||
| ) |
◆ operator>>() [4/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp3_model< n, modulus > & | |||
| ) |
◆ operator>>() [5/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp4_model< n, modulus > & | |||
| ) |
◆ operator>>() [6/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp6_2over3_model< n, modulus > & | |||
| ) |
◆ operator>>() [7/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp6_3over2_model< n, modulus > & | |||
| ) |
◆ operator>>() [8/62]
| std::istream& libff::operator>> | ( | std::istream & | , |
| Fp_model< n, modulus > & | |||
| ) |
◆ operator>>() [9/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| alt_bn128_ate_ell_coeffs & | c | ||
| ) |
◆ operator>>() [10/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| alt_bn128_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [11/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| alt_bn128_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [12/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| alt_bn128_G1 & | g | ||
| ) |
◆ operator>>() [13/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| alt_bn128_G2 & | g | ||
| ) |
◆ operator>>() [14/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_377_ate_ell_coeffs & | c | ||
| ) |
◆ operator>>() [15/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_377_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [16/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_377_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [17/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bls12_377_G1 & | g | ||
| ) |
◆ operator>>() [18/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bls12_377_G2 & | g | ||
| ) |
◆ operator>>() [19/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_381_ate_ell_coeffs & | c | ||
| ) |
◆ operator>>() [20/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_381_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [21/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bls12_381_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [22/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bls12_381_G1 & | g | ||
| ) |
◆ operator>>() [23/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bls12_381_G2 & | g | ||
| ) |
◆ operator>>() [24/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bn128_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [25/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bn128_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [26/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bn128_G1 & | g | ||
| ) |
◆ operator>>() [27/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bn128_G2 & | g | ||
| ) |
◆ operator>>() [28/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bn128_GT & | g | ||
| ) |
◆ operator>>() [29/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bw6_761_ate_ell_coeffs & | c | ||
| ) |
◆ operator>>() [30/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bw6_761_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [31/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bw6_761_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [32/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| bw6_761_ate_G2_precomp_iteration & | prec_Q | ||
| ) |
◆ operator>>() [33/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bw6_761_G1 & | g | ||
| ) |
◆ operator>>() [34/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| bw6_761_G2 & | g | ||
| ) |
◆ operator>>() [35/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| edwards_ate_G1_precomp & | prec_P | ||
| ) |
Definition at line 171 of file edwards_pairing.cpp.
◆ operator>>() [36/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| edwards_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [37/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| edwards_Fq3_conic_coefficients & | cc | ||
| ) |
◆ operator>>() [38/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| edwards_Fq_conic_coefficients & | cc | ||
| ) |
◆ operator>>() [39/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| edwards_G1 & | g | ||
| ) |
◆ operator>>() [40/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| edwards_G2 & | g | ||
| ) |
◆ operator>>() [41/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| edwards_tate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [42/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| edwards_tate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [43/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt4_ate_add_coeffs & | ac | ||
| ) |
◆ operator>>() [44/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt4_ate_dbl_coeffs & | dc | ||
| ) |
◆ operator>>() [45/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt4_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [46/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt4_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [47/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| mnt4_G1 & | g | ||
| ) |
◆ operator>>() [48/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| mnt4_G2 & | g | ||
| ) |
◆ operator>>() [49/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt6_ate_add_coeffs & | ac | ||
| ) |
◆ operator>>() [50/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt6_ate_dbl_coeffs & | dc | ||
| ) |
◆ operator>>() [51/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt6_ate_G1_precomp & | prec_P | ||
| ) |
◆ operator>>() [52/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| mnt6_ate_G2_precomp & | prec_Q | ||
| ) |
◆ operator>>() [53/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| mnt6_G1 & | g | ||
| ) |
◆ operator>>() [54/62]
| std::istream & libff::operator>> | ( | std::istream & | in, |
| mnt6_G2 & | g | ||
| ) |
◆ operator>>() [55/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::map< T1, T2 > & | m | ||
| ) |
◆ operator>>() [56/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::set< T > & | s | ||
| ) |
◆ operator>>() [57/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::vector< Fp12_2over3over2_model< n, modulus >> & | v | ||
| ) |
◆ operator>>() [58/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::vector< Fp2_model< n, modulus >> & | v | ||
| ) |
◆ operator>>() [59/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::vector< Fp3_model< n, modulus >> & | v | ||
| ) |
◆ operator>>() [60/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::vector< Fp6_2over3_model< n, modulus >> & | v | ||
| ) |
◆ operator>>() [61/62]
| std::istream& libff::operator>> | ( | std::istream & | in, |
| std::vector< Fp6_3over2_model< n, modulus >> & | v | ||
| ) |
◆ operator>>() [62/62]
| std::istream& libff::operator>> | ( | std::ostream & | out, |
| std::vector< T > & | v | ||
| ) |
◆ operator^() [1/8]
Definition at line 45 of file bn128_gt.hpp.
◆ operator^() [2/8]
| bn128_GT libff::operator^ | ( | const bn128_GT & | rhs, |
| const Fp_model< m, modulus_p > & | lhs | ||
| ) |
◆ operator^() [3/8]
| Fp12_2over3over2_model<n, modulus> libff::operator^ | ( | const Fp12_2over3over2_model< n, modulus > & | self, |
| const bigint< m > & | exponent | ||
| ) |
◆ operator^() [4/8]
| Fp12_2over3over2_model<n, modulus> libff::operator^ | ( | const Fp12_2over3over2_model< n, modulus > & | self, |
| const Fp_model< m, exp_modulus > & | exponent | ||
| ) |
◆ operator^() [5/8]
| Fp4_model<n, modulus> libff::operator^ | ( | const Fp4_model< n, modulus > & | self, |
| const bigint< m > & | exponent | ||
| ) |
◆ operator^() [6/8]
| Fp4_model<n, modulus> libff::operator^ | ( | const Fp4_model< n, modulus > & | self, |
| const Fp_model< m, modulus_p > & | exponent | ||
| ) |
◆ operator^() [7/8]
| Fp6_2over3_model<n, modulus> libff::operator^ | ( | const Fp6_2over3_model< n, modulus > & | self, |
| const bigint< m > & | exponent | ||
| ) |
◆ operator^() [8/8]
| Fp6_2over3_model<n, modulus> libff::operator^ | ( | const Fp6_2over3_model< n, modulus > & | self, |
| const Fp_model< m, exp_modulus > & | exponent | ||
| ) |
◆ opt_window_wnaf_exp()
| T libff::opt_window_wnaf_exp | ( | const T & | base, |
| const bigint< n > & | scalar, | ||
| const size_t | scalar_bits | ||
| ) |
In additive notation, use wNAF exponentiation (with the window size determined by T) to compute scalar * base.
◆ output_bool()
|
inline |
◆ output_bool_vector()
|
inline |
◆ pack_bit_vector_into_field_element_vector() [1/2]
| std::vector<FieldT> libff::pack_bit_vector_into_field_element_vector | ( | const bit_vector & | v | ) |
◆ pack_bit_vector_into_field_element_vector() [2/2]
| std::vector<FieldT> libff::pack_bit_vector_into_field_element_vector | ( | const bit_vector & | v, |
| const size_t | chunk_bits | ||
| ) |
◆ pack_int_vector_into_field_element_vector()
| std::vector<FieldT> libff::pack_int_vector_into_field_element_vector | ( | const std::vector< size_t > & | v, |
| const size_t | w | ||
| ) |
◆ power() [1/2]
| FieldT libff::power | ( | const FieldT & | base, |
| const bigint< m > & | exponent | ||
| ) |

◆ power() [2/2]
| FieldT libff::power | ( | const FieldT & | base, |
| const unsigned long | exponent | ||
| ) |
◆ print_compilation_info()
| void libff::print_compilation_info | ( | ) |
◆ print_cumulative_op_counts()
| void libff::print_cumulative_op_counts | ( | const bool | only_fq | ) |
◆ print_cumulative_time_entry()
| void libff::print_cumulative_time_entry | ( | const std::string & | key, |
| const long long | factor | ||
| ) |
◆ print_cumulative_times()
| void libff::print_cumulative_times | ( | const long long | factor | ) |
◆ print_header()
| void libff::print_header | ( | const char * | msg | ) |
Definition at line 248 of file profiling.cpp.
◆ print_indent()
| void libff::print_indent | ( | ) |
◆ print_mem()
| void libff::print_mem | ( | const std::string & | s | ) |
◆ print_op_profiling()
| void libff::print_op_profiling | ( | const std::string & | msg | ) |
Definition at line 176 of file profiling.cpp.
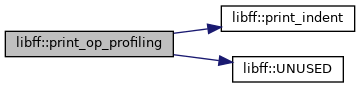
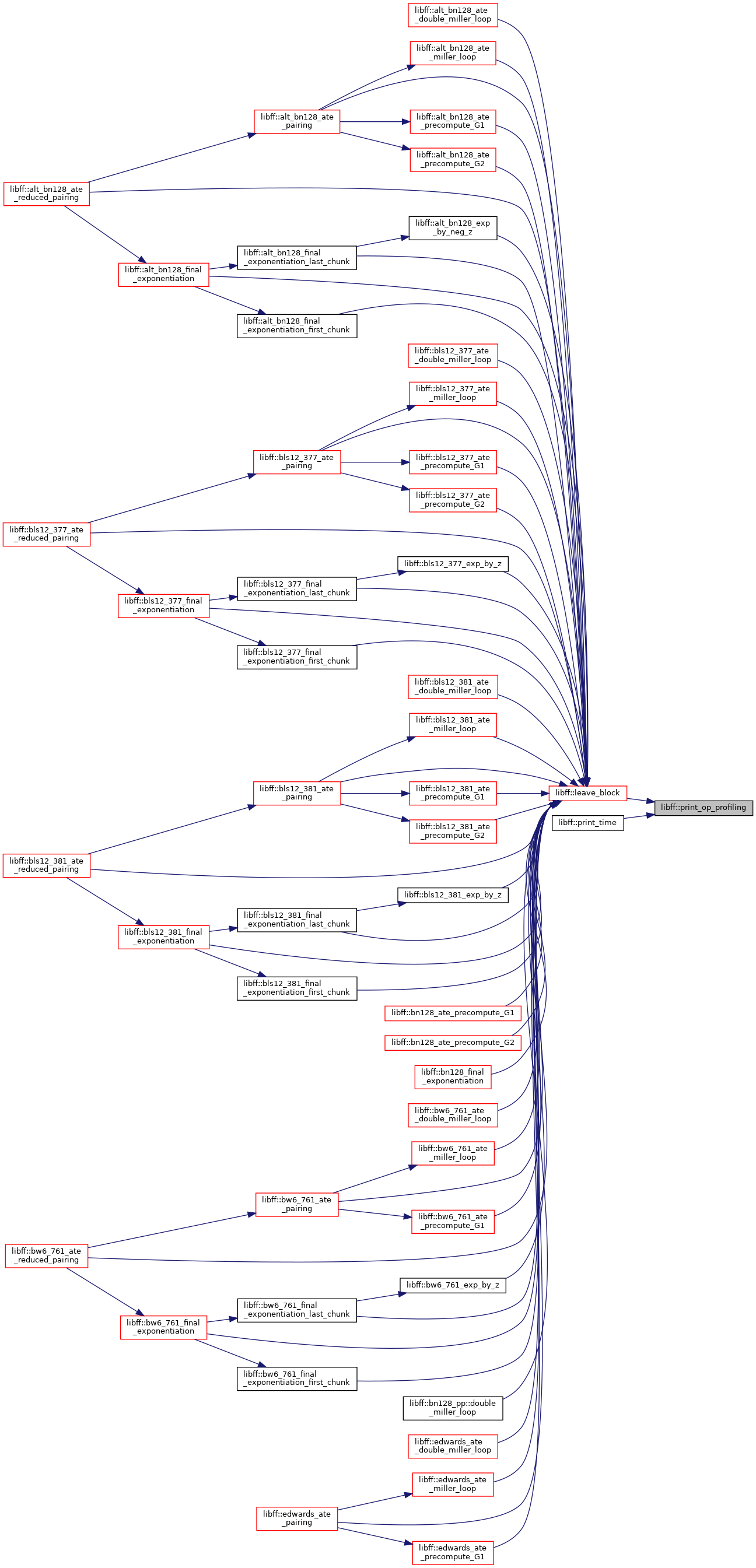
◆ print_time()
| void libff::print_time | ( | const char * | msg | ) |
◆ print_vector()
| void libff::print_vector | ( | const std::vector< FieldT > & | v | ) |
print the elements of a vector
◆ reserialize()
| T libff::reserialize | ( | const T & | obj | ) |
◆ scalar_mul()
| GroupT libff::scalar_mul | ( | const GroupT & | base, |
| const bigint< m > & | scalar | ||
| ) |
◆ serialize_bit_vector()
| void libff::serialize_bit_vector | ( | std::ostream & | out, |
| const bit_vector & | v | ||
| ) |
◆ SHA512_rng()
| FieldT libff::SHA512_rng | ( | const uint64_t | idx | ) |
◆ size_in_bits()
| size_t libff::size_in_bits | ( | const std::vector< T > & | v | ) |
◆ start_profiling()
| void libff::start_profiling | ( | ) |
◆ to_twos_complement()
| size_t libff::to_twos_complement | ( | int | i, |
| size_t | w | ||
| ) |
◆ UNUSED()
| void libff::UNUSED | ( | Types && | ... | ) |
◆ update_wnaf()
| void libff::update_wnaf | ( | std::vector< long > & | naf, |
| const size_t | window_size, | ||
| const bigint< n > & | scalar | ||
| ) |
Find the wNAF representation of the given scalar relative to the given window size, reusing the given vector to store it.
◆ windowed_exp()
| T libff::windowed_exp | ( | const size_t | scalar_size, |
| const size_t | window, | ||
| const window_table< T > & | powers_of_g, | ||
| const FieldT & | pow | ||
| ) |
◆ wnaf_opt_window_size()
| size_t libff::wnaf_opt_window_size | ( | const size_t | scalar_bits | ) |
Compute optimal window size.
Variable Documentation
◆ alt_bn128_ate_is_loop_count_neg
| bool libff::alt_bn128_ate_is_loop_count_neg |
Definition at line 27 of file alt_bn128_init.cpp.
◆ alt_bn128_ate_loop_count
| bigint< alt_bn128_q_limbs > libff::alt_bn128_ate_loop_count |
Definition at line 26 of file alt_bn128_init.cpp.
◆ alt_bn128_coeff_b
| alt_bn128_Fq libff::alt_bn128_coeff_b |
Definition at line 18 of file alt_bn128_init.cpp.
◆ alt_bn128_final_exponent
| bigint< 12 *alt_bn128_q_limbs > libff::alt_bn128_final_exponent |
Definition at line 28 of file alt_bn128_init.cpp.
◆ alt_bn128_final_exponent_is_z_neg
| bool libff::alt_bn128_final_exponent_is_z_neg |
Definition at line 30 of file alt_bn128_init.cpp.
◆ alt_bn128_final_exponent_z
| bigint< alt_bn128_q_limbs > libff::alt_bn128_final_exponent_z |
Definition at line 29 of file alt_bn128_init.cpp.
◆ alt_bn128_modulus_q
| bigint< alt_bn128_q_limbs > libff::alt_bn128_modulus_q |
Definition at line 16 of file alt_bn128_init.cpp.
◆ alt_bn128_modulus_r
| bigint< alt_bn128_r_limbs > libff::alt_bn128_modulus_r |
Definition at line 15 of file alt_bn128_init.cpp.
◆ alt_bn128_q_bitcount
| const mp_size_t libff::alt_bn128_q_bitcount = 254 |
Definition at line 20 of file alt_bn128_init.hpp.
◆ alt_bn128_q_limbs
| const mp_size_t libff::alt_bn128_q_limbs |
Definition at line 24 of file alt_bn128_init.hpp.
◆ alt_bn128_r_bitcount
| const mp_size_t libff::alt_bn128_r_bitcount = 254 |
Definition at line 19 of file alt_bn128_init.hpp.
◆ alt_bn128_r_limbs
| const mp_size_t libff::alt_bn128_r_limbs |
Definition at line 22 of file alt_bn128_init.hpp.
◆ alt_bn128_twist
| alt_bn128_Fq2 libff::alt_bn128_twist |
Definition at line 19 of file alt_bn128_init.cpp.
◆ alt_bn128_twist_coeff_b
| alt_bn128_Fq2 libff::alt_bn128_twist_coeff_b |
Definition at line 20 of file alt_bn128_init.cpp.
◆ alt_bn128_twist_mul_by_b_c0
| alt_bn128_Fq libff::alt_bn128_twist_mul_by_b_c0 |
Definition at line 21 of file alt_bn128_init.cpp.
◆ alt_bn128_twist_mul_by_b_c1
| alt_bn128_Fq libff::alt_bn128_twist_mul_by_b_c1 |
Definition at line 22 of file alt_bn128_init.cpp.
◆ alt_bn128_twist_mul_by_q_X
| alt_bn128_Fq2 libff::alt_bn128_twist_mul_by_q_X |
Definition at line 23 of file alt_bn128_init.cpp.
◆ alt_bn128_twist_mul_by_q_Y
| alt_bn128_Fq2 libff::alt_bn128_twist_mul_by_q_Y |
Definition at line 24 of file alt_bn128_init.cpp.
◆ block_names
| std::vector<std::string> libff::block_names |
Definition at line 88 of file profiling.cpp.
◆ bls12_377_ate_is_loop_count_neg
| bool libff::bls12_377_ate_is_loop_count_neg |
Definition at line 44 of file bls12_377_init.cpp.
◆ bls12_377_ate_loop_count
| bigint< bls12_377_q_limbs > libff::bls12_377_ate_loop_count |
Definition at line 43 of file bls12_377_init.cpp.
◆ bls12_377_coeff_b
| bls12_377_Fq libff::bls12_377_coeff_b |
Definition at line 16 of file bls12_377_init.cpp.
◆ bls12_377_final_exponent
| bigint< 12 *bls12_377_q_limbs > libff::bls12_377_final_exponent |
Definition at line 46 of file bls12_377_init.cpp.
◆ bls12_377_final_exponent_is_z_neg
| bool libff::bls12_377_final_exponent_is_z_neg |
Definition at line 48 of file bls12_377_init.cpp.
◆ bls12_377_final_exponent_z
| bigint< bls12_377_q_limbs > libff::bls12_377_final_exponent_z |
Definition at line 47 of file bls12_377_init.cpp.
◆ bls12_377_g1_endomorphism_beta
| bls12_377_Fq libff::bls12_377_g1_endomorphism_beta |
Definition at line 26 of file bls12_377_init.cpp.
◆ bls12_377_g1_proof_of_safe_subgroup_non_member_x
| bls12_377_Fq libff::bls12_377_g1_proof_of_safe_subgroup_non_member_x |
Definition at line 29 of file bls12_377_init.cpp.
◆ bls12_377_g1_proof_of_safe_subgroup_non_member_y
| bls12_377_Fq libff::bls12_377_g1_proof_of_safe_subgroup_non_member_y |
Definition at line 30 of file bls12_377_init.cpp.
◆ bls12_377_g1_proof_of_safe_subgroup_w
| bigint< bls12_377_r_limbs > libff::bls12_377_g1_proof_of_safe_subgroup_w |
Definition at line 28 of file bls12_377_init.cpp.
◆ bls12_377_g1_safe_subgroup_check_c1
| bigint< bls12_377_r_limbs > libff::bls12_377_g1_safe_subgroup_check_c1 |
Definition at line 27 of file bls12_377_init.cpp.
◆ bls12_377_g2_mul_by_cofactor_h2_0
| bigint< bls12_377_r_limbs > libff::bls12_377_g2_mul_by_cofactor_h2_0 |
Definition at line 40 of file bls12_377_init.cpp.
◆ bls12_377_g2_mul_by_cofactor_h2_1
| bigint< bls12_377_r_limbs > libff::bls12_377_g2_mul_by_cofactor_h2_1 |
Definition at line 41 of file bls12_377_init.cpp.
◆ bls12_377_g2_untwist_frobenius_twist_v
| bls12_377_Fq12 libff::bls12_377_g2_untwist_frobenius_twist_v |
Definition at line 34 of file bls12_377_init.cpp.
◆ bls12_377_g2_untwist_frobenius_twist_v_inverse
| bls12_377_Fq12 libff::bls12_377_g2_untwist_frobenius_twist_v_inverse |
Definition at line 36 of file bls12_377_init.cpp.
◆ bls12_377_g2_untwist_frobenius_twist_w
| bls12_377_Fq12 libff::bls12_377_g2_untwist_frobenius_twist_w |
Definition at line 33 of file bls12_377_init.cpp.
◆ bls12_377_g2_untwist_frobenius_twist_w_3
| bls12_377_Fq12 libff::bls12_377_g2_untwist_frobenius_twist_w_3 |
Definition at line 35 of file bls12_377_init.cpp.
◆ bls12_377_g2_untwist_frobenius_twist_w_3_inverse
| bls12_377_Fq12 libff::bls12_377_g2_untwist_frobenius_twist_w_3_inverse |
Definition at line 37 of file bls12_377_init.cpp.
◆ bls12_377_modulus_r
| bigint< bls12_377_r_limbs > libff::bls12_377_modulus_r |
Definition at line 11 of file bls12_377_init.cpp.
◆ bls12_377_q_bitcount
| const mp_size_t libff::bls12_377_q_bitcount = 377 |
Definition at line 25 of file bls12_377_init.hpp.
◆ bls12_377_q_limbs
| const mp_size_t libff::bls12_377_q_limbs |
Definition at line 29 of file bls12_377_init.hpp.
◆ bls12_377_r_bitcount
| const mp_size_t libff::bls12_377_r_bitcount = 253 |
Definition at line 24 of file bls12_377_init.hpp.
◆ bls12_377_r_limbs
| const mp_size_t libff::bls12_377_r_limbs |
Definition at line 27 of file bls12_377_init.hpp.
◆ bls12_377_trace_of_frobenius
| bigint< bls12_377_r_limbs > libff::bls12_377_trace_of_frobenius |
Definition at line 17 of file bls12_377_init.cpp.
◆ bls12_377_twist
| bls12_377_Fq2 libff::bls12_377_twist |
Definition at line 18 of file bls12_377_init.cpp.
◆ bls12_377_twist_coeff_b
| bls12_377_Fq2 libff::bls12_377_twist_coeff_b |
Definition at line 19 of file bls12_377_init.cpp.
◆ bls12_377_twist_mul_by_b_c0
| bls12_377_Fq libff::bls12_377_twist_mul_by_b_c0 |
Definition at line 20 of file bls12_377_init.cpp.
◆ bls12_377_twist_mul_by_b_c1
| bls12_377_Fq libff::bls12_377_twist_mul_by_b_c1 |
Definition at line 21 of file bls12_377_init.cpp.
◆ bls12_377_twist_mul_by_q_X
| bls12_377_Fq2 libff::bls12_377_twist_mul_by_q_X |
Definition at line 22 of file bls12_377_init.cpp.
◆ bls12_377_twist_mul_by_q_Y
| bls12_377_Fq2 libff::bls12_377_twist_mul_by_q_Y |
Definition at line 23 of file bls12_377_init.cpp.
◆ bls12_381_ate_is_loop_count_neg
| bool libff::bls12_381_ate_is_loop_count_neg |
Definition at line 21 of file bls12_381_init.cpp.
◆ bls12_381_ate_loop_count
| bigint< bls12_381_q_limbs > libff::bls12_381_ate_loop_count |
Definition at line 20 of file bls12_381_init.cpp.
◆ bls12_381_coeff_b
| bls12_381_Fq libff::bls12_381_coeff_b |
Definition at line 11 of file bls12_381_init.cpp.
◆ bls12_381_final_exponent
| bigint< 12 *bls12_381_q_limbs > libff::bls12_381_final_exponent |
Definition at line 22 of file bls12_381_init.cpp.
◆ bls12_381_final_exponent_is_z_neg
| bool libff::bls12_381_final_exponent_is_z_neg |
Definition at line 24 of file bls12_381_init.cpp.
◆ bls12_381_final_exponent_z
| bigint< bls12_381_q_limbs > libff::bls12_381_final_exponent_z |
Definition at line 23 of file bls12_381_init.cpp.
◆ bls12_381_modulus_q
| bigint< bls12_381_q_limbs > libff::bls12_381_modulus_q |
Definition at line 9 of file bls12_381_init.cpp.
◆ bls12_381_modulus_r
| bigint< bls12_381_r_limbs > libff::bls12_381_modulus_r |
Definition at line 8 of file bls12_381_init.cpp.
◆ bls12_381_q_bitcount
| const mp_size_t libff::bls12_381_q_bitcount = 381 |
Definition at line 20 of file bls12_381_init.hpp.
◆ bls12_381_q_limbs
| const mp_size_t libff::bls12_381_q_limbs |
Definition at line 24 of file bls12_381_init.hpp.
◆ bls12_381_r_bitcount
| const mp_size_t libff::bls12_381_r_bitcount = 255 |
Definition at line 19 of file bls12_381_init.hpp.
◆ bls12_381_r_limbs
| const mp_size_t libff::bls12_381_r_limbs |
Definition at line 22 of file bls12_381_init.hpp.
◆ bls12_381_trace_of_frobenius
| bigint< bls12_381_r_limbs > libff::bls12_381_trace_of_frobenius |
Definition at line 12 of file bls12_381_init.cpp.
◆ bls12_381_twist
| bls12_381_Fq2 libff::bls12_381_twist |
Definition at line 13 of file bls12_381_init.cpp.
◆ bls12_381_twist_coeff_b
| bls12_381_Fq2 libff::bls12_381_twist_coeff_b |
Definition at line 14 of file bls12_381_init.cpp.
◆ bls12_381_twist_mul_by_b_c0
| bls12_381_Fq libff::bls12_381_twist_mul_by_b_c0 |
Definition at line 15 of file bls12_381_init.cpp.
◆ bls12_381_twist_mul_by_b_c1
| bls12_381_Fq libff::bls12_381_twist_mul_by_b_c1 |
Definition at line 16 of file bls12_381_init.cpp.
◆ bls12_381_twist_mul_by_q_X
| bls12_381_Fq2 libff::bls12_381_twist_mul_by_q_X |
Definition at line 17 of file bls12_381_init.cpp.
◆ bls12_381_twist_mul_by_q_Y
| bls12_381_Fq2 libff::bls12_381_twist_mul_by_q_Y |
Definition at line 18 of file bls12_381_init.cpp.
◆ bn128_coeff_b
| bn::Fp libff::bn128_coeff_b |
Definition at line 19 of file bn128_init.cpp.
◆ bn128_Fq2_nqr_to_t
| bn::Fp2 libff::bn128_Fq2_nqr_to_t |
Definition at line 26 of file bn128_init.cpp.
◆ bn128_Fq2_s
| size_t libff::bn128_Fq2_s |
Definition at line 25 of file bn128_init.cpp.
◆ bn128_Fq2_t_minus_1_over_2
| mie::Vuint libff::bn128_Fq2_t_minus_1_over_2 |
Definition at line 27 of file bn128_init.cpp.
◆ bn128_Fq_nqr_to_t
| bn::Fp libff::bn128_Fq_nqr_to_t |
Definition at line 21 of file bn128_init.cpp.
◆ bn128_Fq_s
| size_t libff::bn128_Fq_s |
Definition at line 20 of file bn128_init.cpp.
◆ bn128_Fq_t_minus_1_over_2
| mie::Vuint libff::bn128_Fq_t_minus_1_over_2 |
Definition at line 22 of file bn128_init.cpp.
◆ bn128_modulus_q
| bigint< bn128_q_limbs > libff::bn128_modulus_q |
Definition at line 17 of file bn128_init.cpp.
◆ bn128_modulus_r
| bigint< bn128_r_limbs > libff::bn128_modulus_r |
Definition at line 16 of file bn128_init.cpp.
◆ bn128_q_bitcount
| const mp_size_t libff::bn128_q_bitcount = 254 |
Definition at line 19 of file bn128_init.hpp.
◆ bn128_q_limbs
| const mp_size_t libff::bn128_q_limbs |
Definition at line 23 of file bn128_init.hpp.
◆ bn128_r_bitcount
| const mp_size_t libff::bn128_r_bitcount = 254 |
Definition at line 18 of file bn128_init.hpp.
◆ bn128_r_limbs
| const mp_size_t libff::bn128_r_limbs |
Definition at line 21 of file bn128_init.hpp.
◆ bn128_twist_coeff_b
| bn::Fp2 libff::bn128_twist_coeff_b |
Definition at line 24 of file bn128_init.cpp.
◆ bw6_761_ate_is_loop_count_neg
| bool libff::bw6_761_ate_is_loop_count_neg |
Definition at line 23 of file bw6_761_init.cpp.
◆ bw6_761_ate_loop_count1
| bigint< bw6_761_q_limbs > libff::bw6_761_ate_loop_count1 |
Definition at line 21 of file bw6_761_init.cpp.
◆ bw6_761_ate_loop_count2
| bigint< bw6_761_q_limbs > libff::bw6_761_ate_loop_count2 |
Definition at line 22 of file bw6_761_init.cpp.
◆ bw6_761_coeff_b
| bw6_761_Fq libff::bw6_761_coeff_b |
Definition at line 17 of file bw6_761_init.cpp.
◆ bw6_761_final_exponent_is_z_neg
| bool libff::bw6_761_final_exponent_is_z_neg |
Definition at line 25 of file bw6_761_init.cpp.
◆ bw6_761_final_exponent_z
| bigint< bw6_761_q_limbs > libff::bw6_761_final_exponent_z |
Definition at line 24 of file bw6_761_init.cpp.
◆ bw6_761_modulus_q
| bigint< bw6_761_q_limbs > libff::bw6_761_modulus_q |
Definition at line 15 of file bw6_761_init.cpp.
◆ bw6_761_modulus_r
| bigint< bw6_761_r_limbs > libff::bw6_761_modulus_r |
Definition at line 14 of file bw6_761_init.cpp.
◆ bw6_761_q_bitcount
| const mp_size_t libff::bw6_761_q_bitcount = 761 |
Definition at line 13 of file bw6_761_init.hpp.
◆ bw6_761_q_limbs
| const mp_size_t libff::bw6_761_q_limbs |
Definition at line 17 of file bw6_761_init.hpp.
◆ bw6_761_r_bitcount
| const mp_size_t libff::bw6_761_r_bitcount = 377 |
Definition at line 12 of file bw6_761_init.hpp.
◆ bw6_761_r_limbs
| const mp_size_t libff::bw6_761_r_limbs |
Definition at line 15 of file bw6_761_init.hpp.
◆ bw6_761_twist
| bw6_761_Fq libff::bw6_761_twist |
Definition at line 18 of file bw6_761_init.cpp.
◆ bw6_761_twist_coeff_b
| bw6_761_Fq libff::bw6_761_twist_coeff_b |
Definition at line 19 of file bw6_761_init.cpp.
◆ cumulative_op_counts
| std::map<std::pair<std::string, std::string>, long long> libff::cumulative_op_counts |
Definition at line 83 of file profiling.cpp.
◆ cumulative_times
| std::map< std::string, long long > libff::cumulative_times |
Definition at line 76 of file profiling.cpp.
◆ curve_point_y_at_x
| decltype(((GroupT *)nullptr)->X) libff::curve_point_y_at_x(const decltype(((GroupT *) nullptr) ->X) &x) |
Definition at line 24 of file curve_utils.hpp.
◆ DEFAULT_COMPRESSION
|
constexpr |
Definition at line 60 of file serialization.hpp.
◆ DEFAULT_ENCODING
|
constexpr |
Definition at line 48 of file serialization.hpp.
◆ DEFAULT_FORM
|
constexpr |
Definition at line 54 of file serialization.hpp.
◆ edwards_ate_loop_count
| bigint< edwards_q_limbs > libff::edwards_ate_loop_count |
Definition at line 32 of file edwards_init.cpp.
◆ edwards_coeff_a
| edwards_Fq libff::edwards_coeff_a |
Definition at line 18 of file edwards_init.cpp.
◆ edwards_coeff_d
| edwards_Fq libff::edwards_coeff_d |
Definition at line 19 of file edwards_init.cpp.
◆ edwards_final_exponent
| bigint< 6 *edwards_q_limbs > libff::edwards_final_exponent |
Definition at line 33 of file edwards_init.cpp.
◆ edwards_final_exponent_last_chunk_abs_of_w0
| bigint< edwards_q_limbs > libff::edwards_final_exponent_last_chunk_abs_of_w0 |
Definition at line 34 of file edwards_init.cpp.
◆ edwards_final_exponent_last_chunk_is_w0_neg
| bool libff::edwards_final_exponent_last_chunk_is_w0_neg |
Definition at line 35 of file edwards_init.cpp.
◆ edwards_final_exponent_last_chunk_w1
| bigint< edwards_q_limbs > libff::edwards_final_exponent_last_chunk_w1 |
Definition at line 36 of file edwards_init.cpp.
◆ edwards_modulus_q
| bigint< edwards_q_limbs > libff::edwards_modulus_q |
Definition at line 16 of file edwards_init.cpp.
◆ edwards_modulus_r
| bigint< edwards_r_limbs > libff::edwards_modulus_r |
Definition at line 15 of file edwards_init.cpp.
◆ edwards_q_bitcount
| const mp_size_t libff::edwards_q_bitcount = 183 |
Definition at line 19 of file edwards_init.hpp.
◆ edwards_q_limbs
| const mp_size_t libff::edwards_q_limbs |
Definition at line 23 of file edwards_init.hpp.
◆ edwards_r_bitcount
| const mp_size_t libff::edwards_r_bitcount = 181 |
Definition at line 18 of file edwards_init.hpp.
◆ edwards_r_limbs
| const mp_size_t libff::edwards_r_limbs |
Definition at line 21 of file edwards_init.hpp.
◆ edwards_twist
| edwards_Fq3 libff::edwards_twist |
Definition at line 20 of file edwards_init.cpp.
◆ edwards_twist_coeff_a
| edwards_Fq3 libff::edwards_twist_coeff_a |
Definition at line 21 of file edwards_init.cpp.
◆ edwards_twist_coeff_d
| edwards_Fq3 libff::edwards_twist_coeff_d |
Definition at line 22 of file edwards_init.cpp.
◆ edwards_twist_mul_by_a_c0
| edwards_Fq libff::edwards_twist_mul_by_a_c0 |
Definition at line 23 of file edwards_init.cpp.
◆ edwards_twist_mul_by_a_c1
| edwards_Fq libff::edwards_twist_mul_by_a_c1 |
Definition at line 24 of file edwards_init.cpp.
◆ edwards_twist_mul_by_a_c2
| edwards_Fq libff::edwards_twist_mul_by_a_c2 |
Definition at line 25 of file edwards_init.cpp.
◆ edwards_twist_mul_by_d_c0
| edwards_Fq libff::edwards_twist_mul_by_d_c0 |
Definition at line 26 of file edwards_init.cpp.
◆ edwards_twist_mul_by_d_c1
| edwards_Fq libff::edwards_twist_mul_by_d_c1 |
Definition at line 27 of file edwards_init.cpp.
◆ edwards_twist_mul_by_d_c2
| edwards_Fq libff::edwards_twist_mul_by_d_c2 |
Definition at line 28 of file edwards_init.cpp.
◆ edwards_twist_mul_by_q_Y
| edwards_Fq libff::edwards_twist_mul_by_q_Y |
Definition at line 29 of file edwards_init.cpp.
◆ edwards_twist_mul_by_q_Z
| edwards_Fq libff::edwards_twist_mul_by_q_Z |
Definition at line 30 of file edwards_init.cpp.
◆ enter_cpu_times
| std::map<std::string, long long> libff::enter_cpu_times |
Definition at line 79 of file profiling.cpp.
◆ enter_times
| std::map<std::string, long long> libff::enter_times |
Definition at line 74 of file profiling.cpp.
◆ indentation
| size_t libff::indentation = 0 |
Definition at line 86 of file profiling.cpp.
◆ inhibit_profiling_counters
| bool libff::inhibit_profiling_counters = false |
Definition at line 108 of file profiling.cpp.
◆ inhibit_profiling_info
| bool libff::inhibit_profiling_info = false |
Definition at line 107 of file profiling.cpp.
◆ invocation_counts
| std::map< std::string, size_t > libff::invocation_counts |
Definition at line 73 of file profiling.cpp.
◆ last_cpu_time
| long long libff::last_cpu_time |
Definition at line 63 of file profiling.cpp.
◆ last_cpu_times
| std::map<std::string, long long> libff::last_cpu_times |
Definition at line 80 of file profiling.cpp.
◆ last_time
| long long libff::last_time |
Definition at line 62 of file profiling.cpp.
◆ last_times
| std::map< std::string, long long > libff::last_times |
Definition at line 75 of file profiling.cpp.
◆ mnt46_A_bitcount
| const mp_size_t libff::mnt46_A_bitcount = 298 |
Definition at line 20 of file mnt46_common.hpp.
◆ mnt46_A_limbs
| const mp_size_t libff::mnt46_A_limbs |
Definition at line 23 of file mnt46_common.hpp.
◆ mnt46_B_bitcount
| const mp_size_t libff::mnt46_B_bitcount = 298 |
Definition at line 21 of file mnt46_common.hpp.
◆ mnt46_B_limbs
| const mp_size_t libff::mnt46_B_limbs |
Definition at line 25 of file mnt46_common.hpp.
◆ mnt46_modulus_A
| bigint< mnt46_A_limbs > libff::mnt46_modulus_A |
Definition at line 19 of file mnt46_common.cpp.
◆ mnt46_modulus_B
| bigint< mnt46_B_limbs > libff::mnt46_modulus_B |
Definition at line 20 of file mnt46_common.cpp.
◆ mnt4_ate_is_loop_count_neg
| bool libff::mnt4_ate_is_loop_count_neg |
Definition at line 35 of file mnt4_init.cpp.
◆ mnt4_ate_loop_count
| bigint< mnt4_q_limbs > libff::mnt4_ate_loop_count |
Definition at line 34 of file mnt4_init.cpp.
◆ mnt4_final_exponent
| bigint< 4 *mnt4_q_limbs > libff::mnt4_final_exponent |
Definition at line 36 of file mnt4_init.cpp.
◆ mnt4_final_exponent_last_chunk_abs_of_w0
| bigint< mnt4_q_limbs > libff::mnt4_final_exponent_last_chunk_abs_of_w0 |
Definition at line 37 of file mnt4_init.cpp.
◆ mnt4_final_exponent_last_chunk_is_w0_neg
| bool libff::mnt4_final_exponent_last_chunk_is_w0_neg |
Definition at line 38 of file mnt4_init.cpp.
◆ mnt4_final_exponent_last_chunk_w1
| bigint< mnt4_q_limbs > libff::mnt4_final_exponent_last_chunk_w1 |
Definition at line 39 of file mnt4_init.cpp.
◆ mnt4_modulus_q
| bigint<mnt4_q_limbs> libff::mnt4_modulus_q |
◆ mnt4_modulus_r
| bigint<mnt4_r_limbs> libff::mnt4_modulus_r |
◆ mnt4_q_bitcount
| const mp_size_t libff::mnt4_q_bitcount = mnt46_B_bitcount |
Definition at line 28 of file mnt4_init.hpp.
◆ mnt4_q_limbs
| const mp_size_t libff::mnt4_q_limbs = mnt46_B_limbs |
Definition at line 31 of file mnt4_init.hpp.
◆ mnt4_r_bitcount
| const mp_size_t libff::mnt4_r_bitcount = mnt46_A_bitcount |
Definition at line 27 of file mnt4_init.hpp.
◆ mnt4_r_limbs
| const mp_size_t libff::mnt4_r_limbs = mnt46_A_limbs |
Definition at line 30 of file mnt4_init.hpp.
◆ mnt4_twist
| mnt4_Fq2 libff::mnt4_twist |
Definition at line 24 of file mnt4_init.cpp.
◆ mnt4_twist_coeff_a
| mnt4_Fq2 libff::mnt4_twist_coeff_a |
Definition at line 25 of file mnt4_init.cpp.
◆ mnt4_twist_coeff_b
| mnt4_Fq2 libff::mnt4_twist_coeff_b |
Definition at line 26 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_a_c0
| mnt4_Fq libff::mnt4_twist_mul_by_a_c0 |
Definition at line 27 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_a_c1
| mnt4_Fq libff::mnt4_twist_mul_by_a_c1 |
Definition at line 28 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_b_c0
| mnt4_Fq libff::mnt4_twist_mul_by_b_c0 |
Definition at line 29 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_b_c1
| mnt4_Fq libff::mnt4_twist_mul_by_b_c1 |
Definition at line 30 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_q_X
| mnt4_Fq libff::mnt4_twist_mul_by_q_X |
Definition at line 31 of file mnt4_init.cpp.
◆ mnt4_twist_mul_by_q_Y
| mnt4_Fq libff::mnt4_twist_mul_by_q_Y |
Definition at line 32 of file mnt4_init.cpp.
◆ mnt6_ate_is_loop_count_neg
| bool libff::mnt6_ate_is_loop_count_neg |
Definition at line 37 of file mnt6_init.cpp.
◆ mnt6_ate_loop_count
| bigint< mnt6_q_limbs > libff::mnt6_ate_loop_count |
Definition at line 36 of file mnt6_init.cpp.
◆ mnt6_final_exponent
| bigint< 6 *mnt6_q_limbs > libff::mnt6_final_exponent |
Definition at line 38 of file mnt6_init.cpp.
◆ mnt6_final_exponent_last_chunk_abs_of_w0
| bigint< mnt6_q_limbs > libff::mnt6_final_exponent_last_chunk_abs_of_w0 |
Definition at line 39 of file mnt6_init.cpp.
◆ mnt6_final_exponent_last_chunk_is_w0_neg
| bool libff::mnt6_final_exponent_last_chunk_is_w0_neg |
Definition at line 40 of file mnt6_init.cpp.
◆ mnt6_final_exponent_last_chunk_w1
| bigint< mnt6_q_limbs > libff::mnt6_final_exponent_last_chunk_w1 |
Definition at line 41 of file mnt6_init.cpp.
◆ mnt6_modulus_q
| bigint<mnt6_q_limbs> libff::mnt6_modulus_q |
◆ mnt6_modulus_r
| bigint<mnt6_r_limbs> libff::mnt6_modulus_r |
◆ mnt6_q_bitcount
| const mp_size_t libff::mnt6_q_bitcount = mnt46_A_bitcount |
Definition at line 28 of file mnt6_init.hpp.
◆ mnt6_q_limbs
| const mp_size_t libff::mnt6_q_limbs = mnt46_A_limbs |
Definition at line 31 of file mnt6_init.hpp.
◆ mnt6_r_bitcount
| const mp_size_t libff::mnt6_r_bitcount = mnt46_B_bitcount |
Definition at line 27 of file mnt6_init.hpp.
◆ mnt6_r_limbs
| const mp_size_t libff::mnt6_r_limbs = mnt46_B_limbs |
Definition at line 30 of file mnt6_init.hpp.
◆ mnt6_twist
| mnt6_Fq3 libff::mnt6_twist |
Definition at line 24 of file mnt6_init.cpp.
◆ mnt6_twist_coeff_a
| mnt6_Fq3 libff::mnt6_twist_coeff_a |
Definition at line 25 of file mnt6_init.cpp.
◆ mnt6_twist_coeff_b
| mnt6_Fq3 libff::mnt6_twist_coeff_b |
Definition at line 26 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_a_c0
| mnt6_Fq libff::mnt6_twist_mul_by_a_c0 |
Definition at line 27 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_a_c1
| mnt6_Fq libff::mnt6_twist_mul_by_a_c1 |
Definition at line 28 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_a_c2
| mnt6_Fq libff::mnt6_twist_mul_by_a_c2 |
Definition at line 29 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_b_c0
| mnt6_Fq libff::mnt6_twist_mul_by_b_c0 |
Definition at line 30 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_b_c1
| mnt6_Fq libff::mnt6_twist_mul_by_b_c1 |
Definition at line 31 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_b_c2
| mnt6_Fq libff::mnt6_twist_mul_by_b_c2 |
Definition at line 32 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_q_X
| mnt6_Fq libff::mnt6_twist_mul_by_q_X |
Definition at line 33 of file mnt6_init.cpp.
◆ mnt6_twist_mul_by_q_Y
| mnt6_Fq libff::mnt6_twist_mul_by_q_Y |
Definition at line 34 of file mnt6_init.cpp.
◆ op_counts
| std::map<std::pair<std::string, std::string>, long long> libff::op_counts |
Definition at line 81 of file profiling.cpp.
◆ op_data_points
| std::list<std::pair<std::string, long long *> > libff::op_data_points |
Definition at line 90 of file profiling.cpp.
◆ start_cpu_time
| long long libff::start_cpu_time |
Definition at line 63 of file profiling.cpp.
◆ start_time
| long long libff::start_time |
Definition at line 62 of file profiling.cpp.



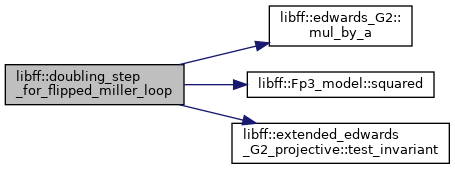


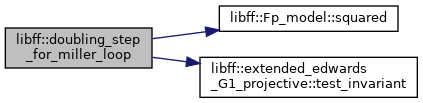
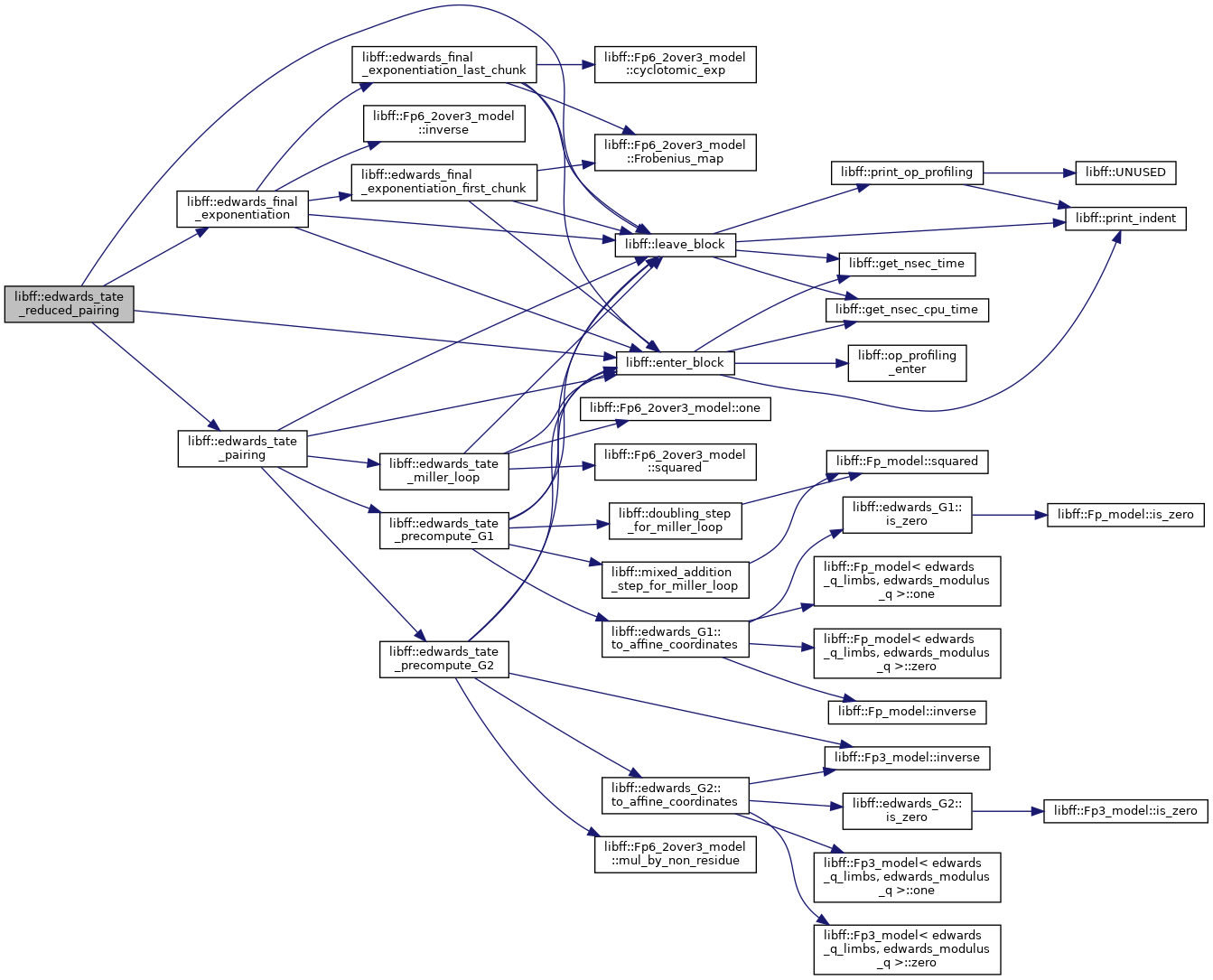

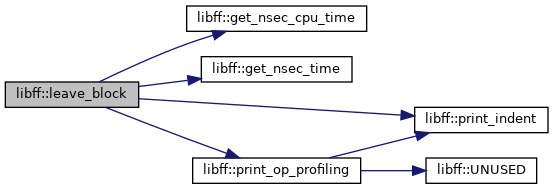
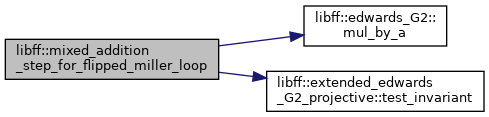



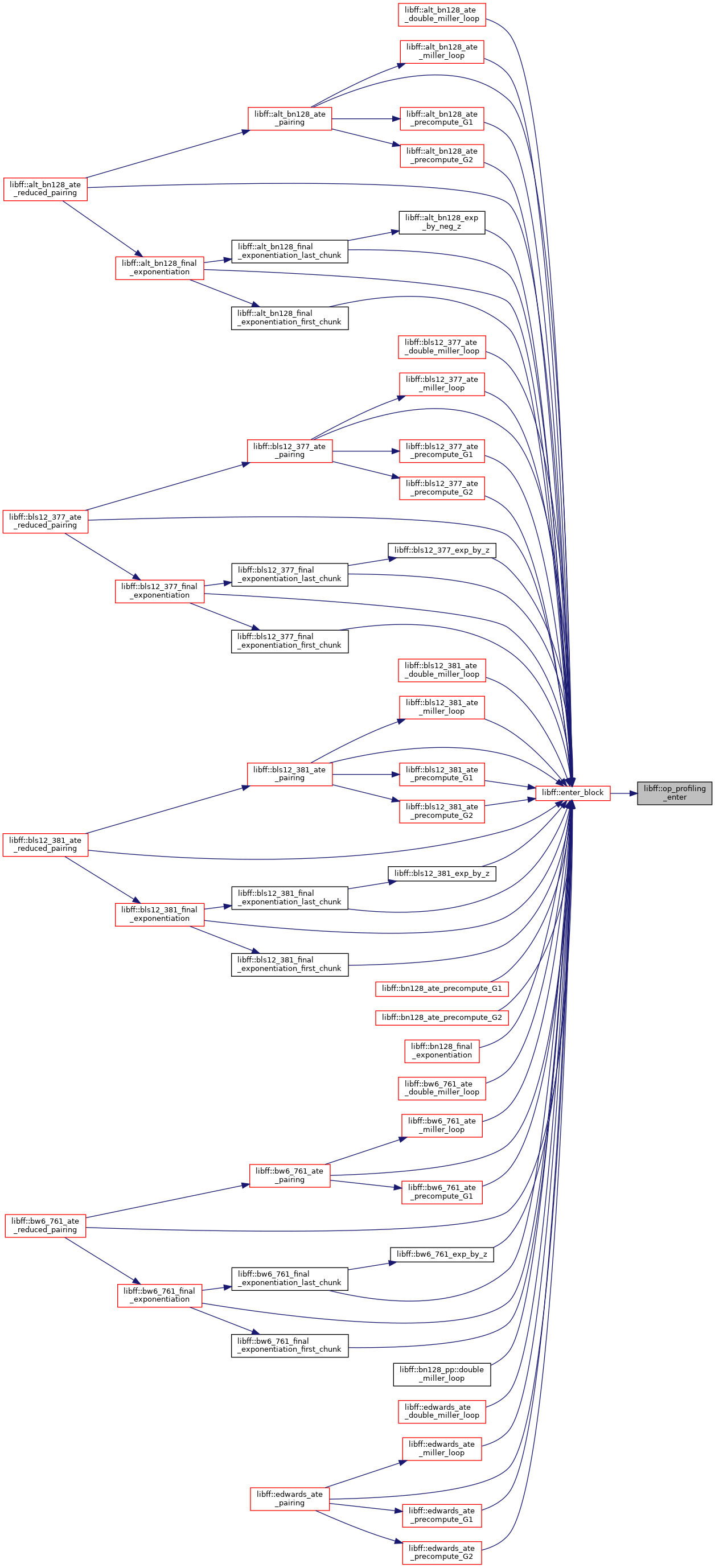
















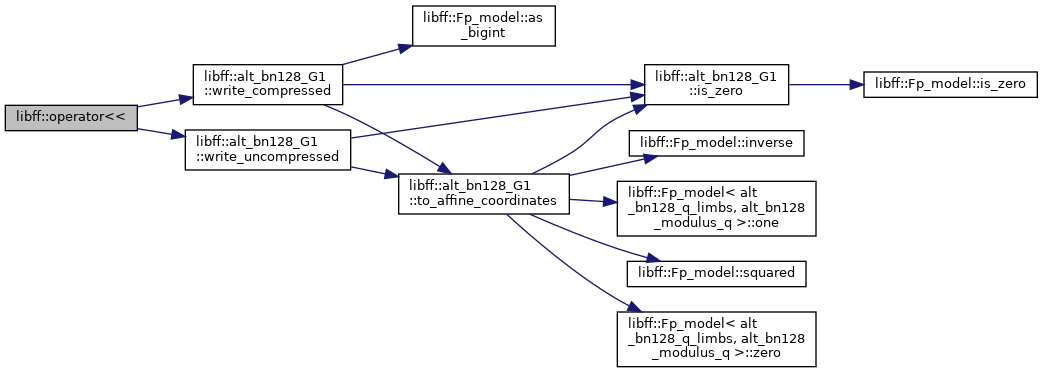
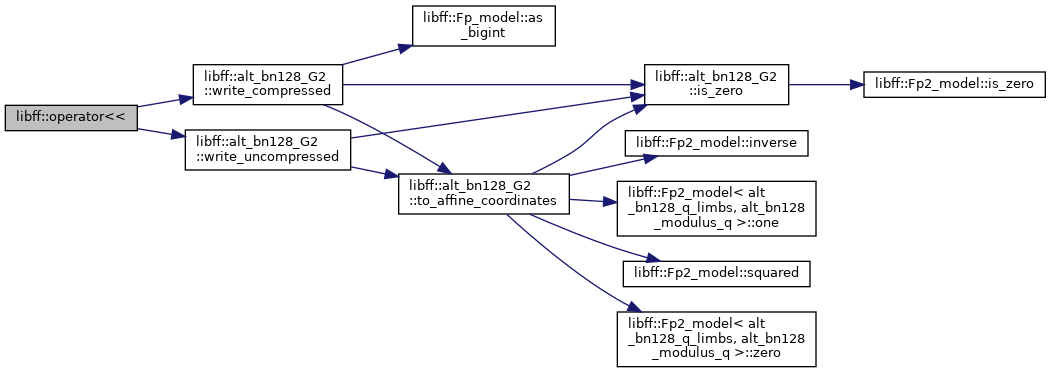
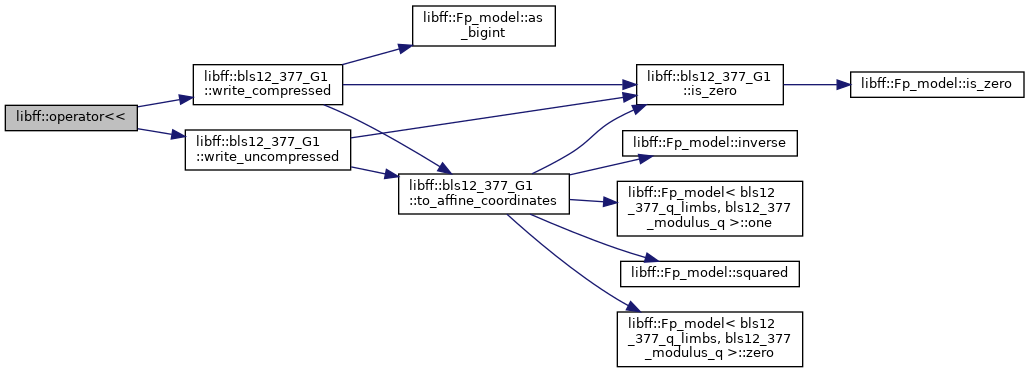
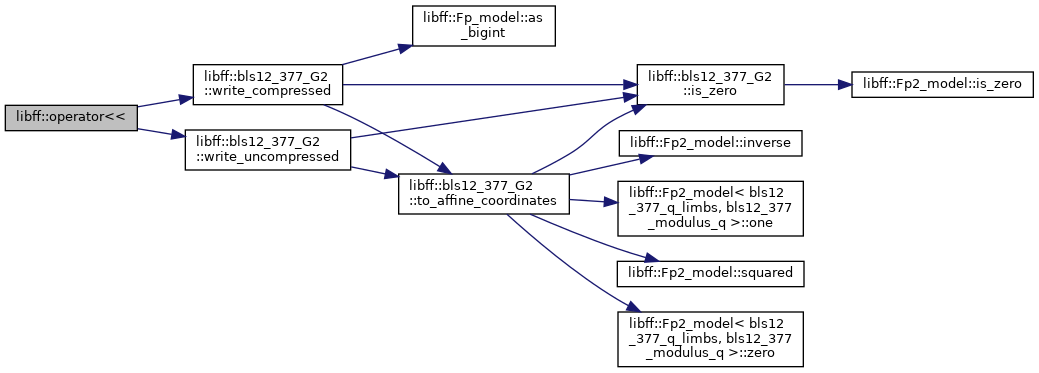
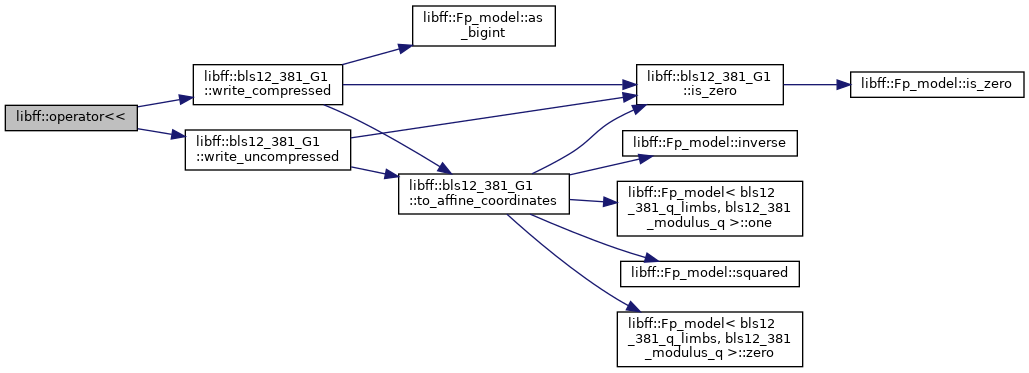
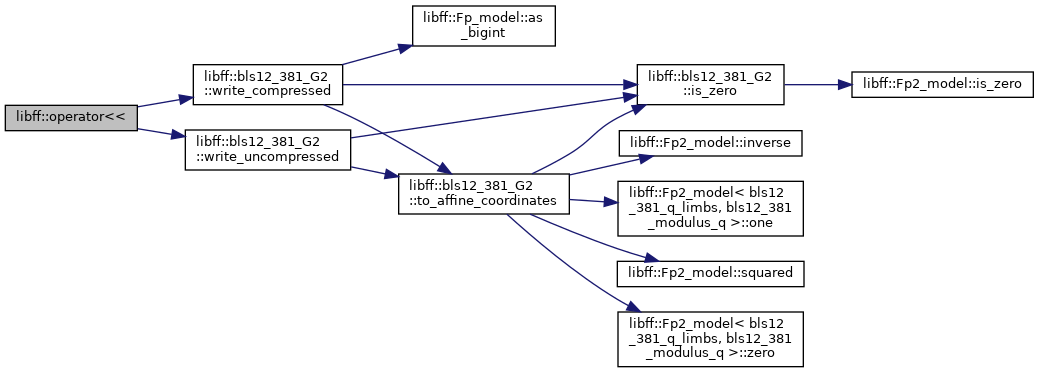


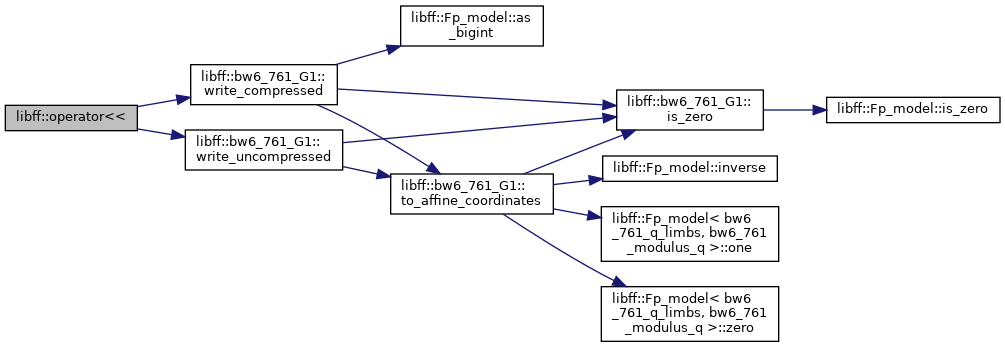
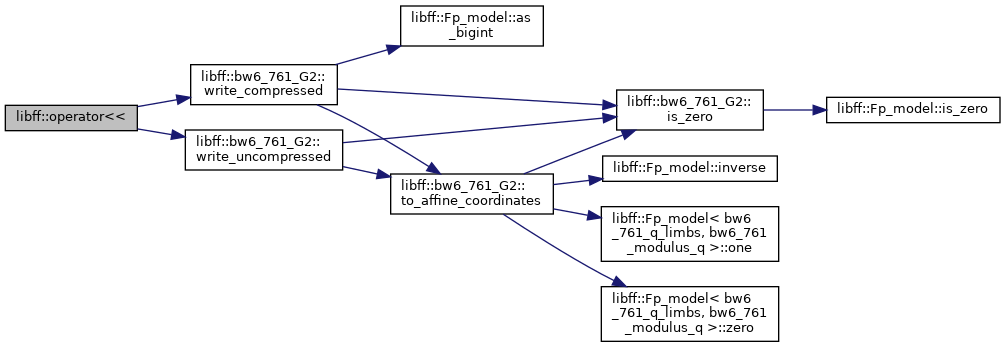
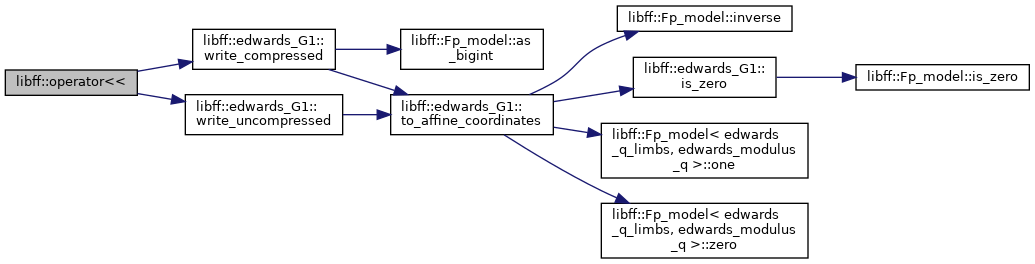
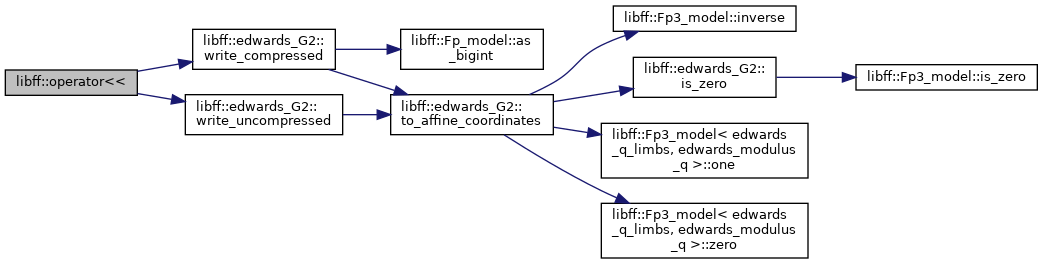
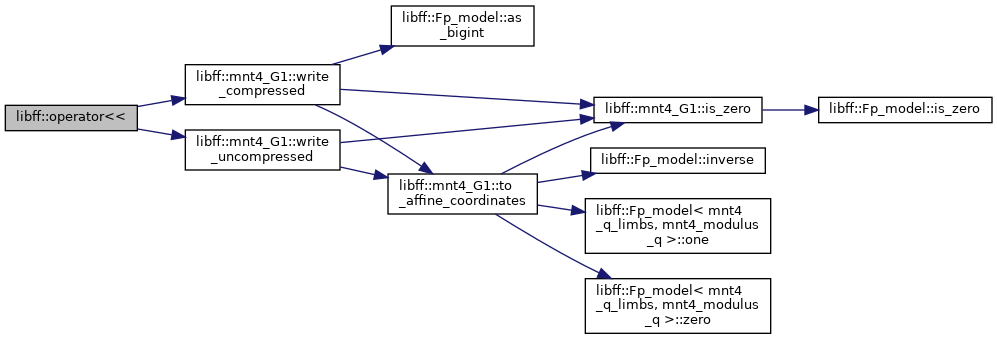
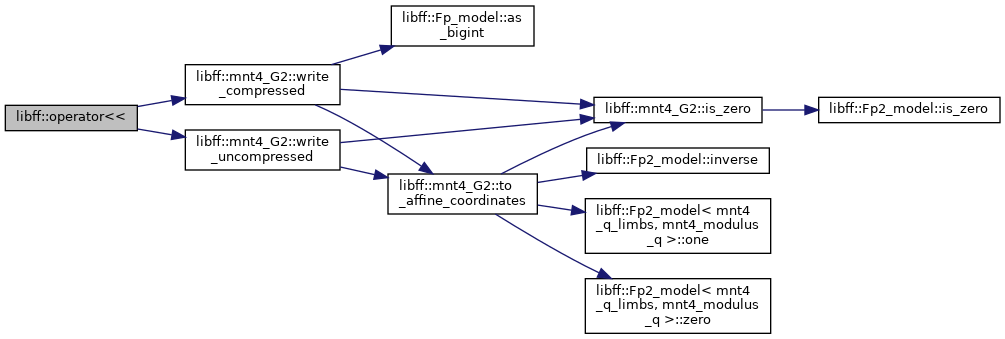
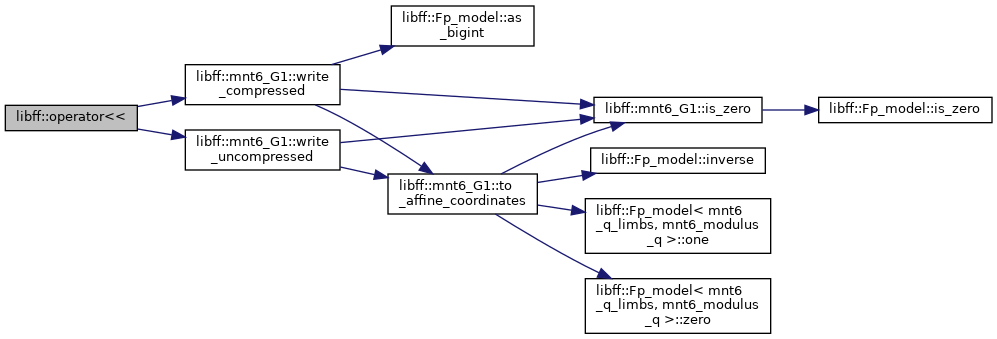
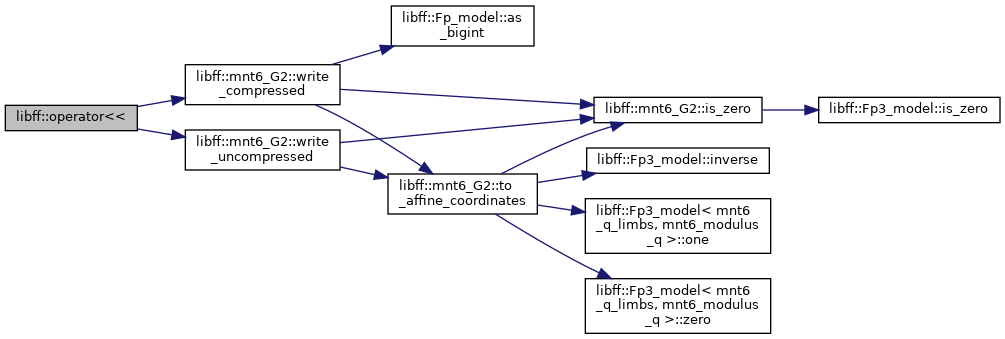


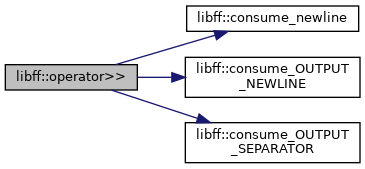
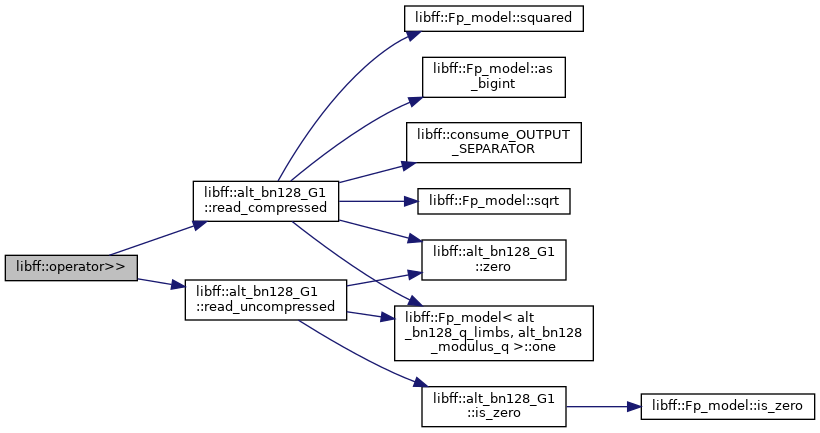
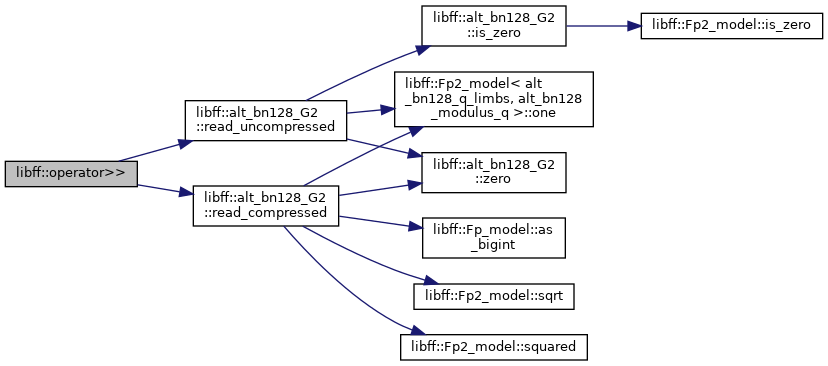




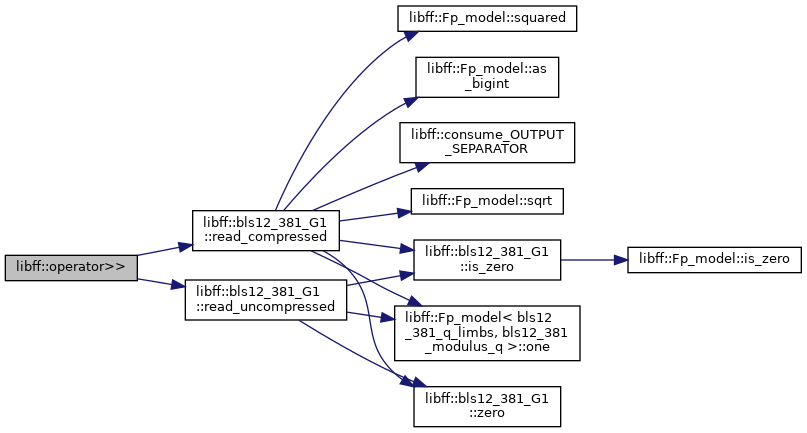
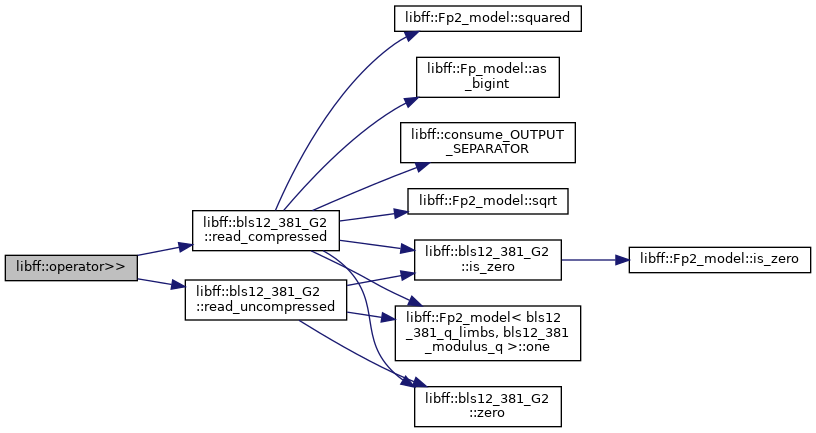


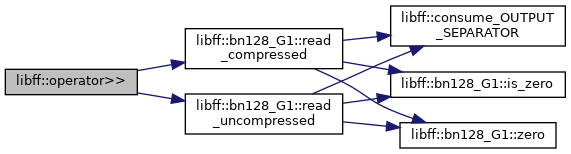
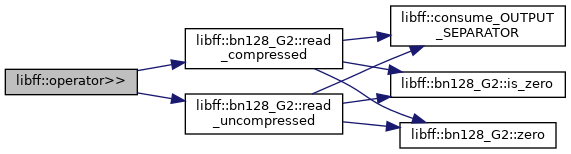












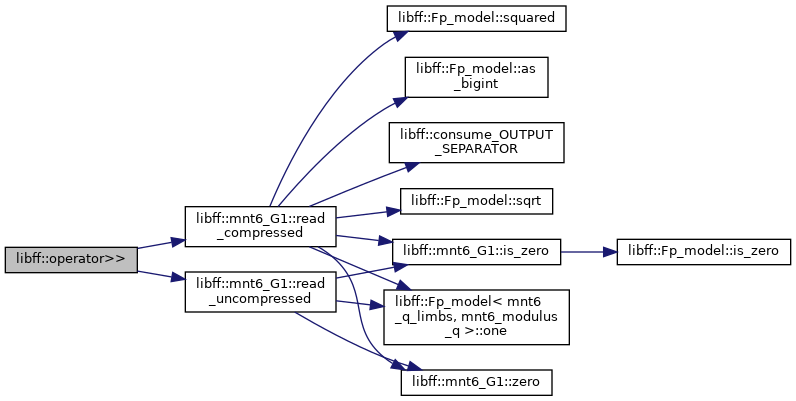
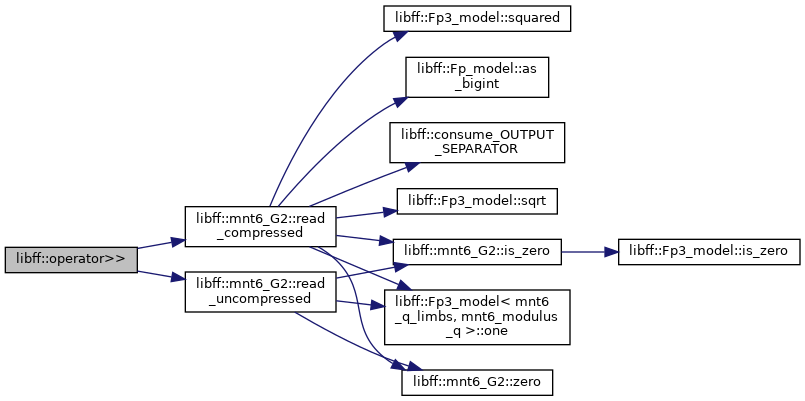





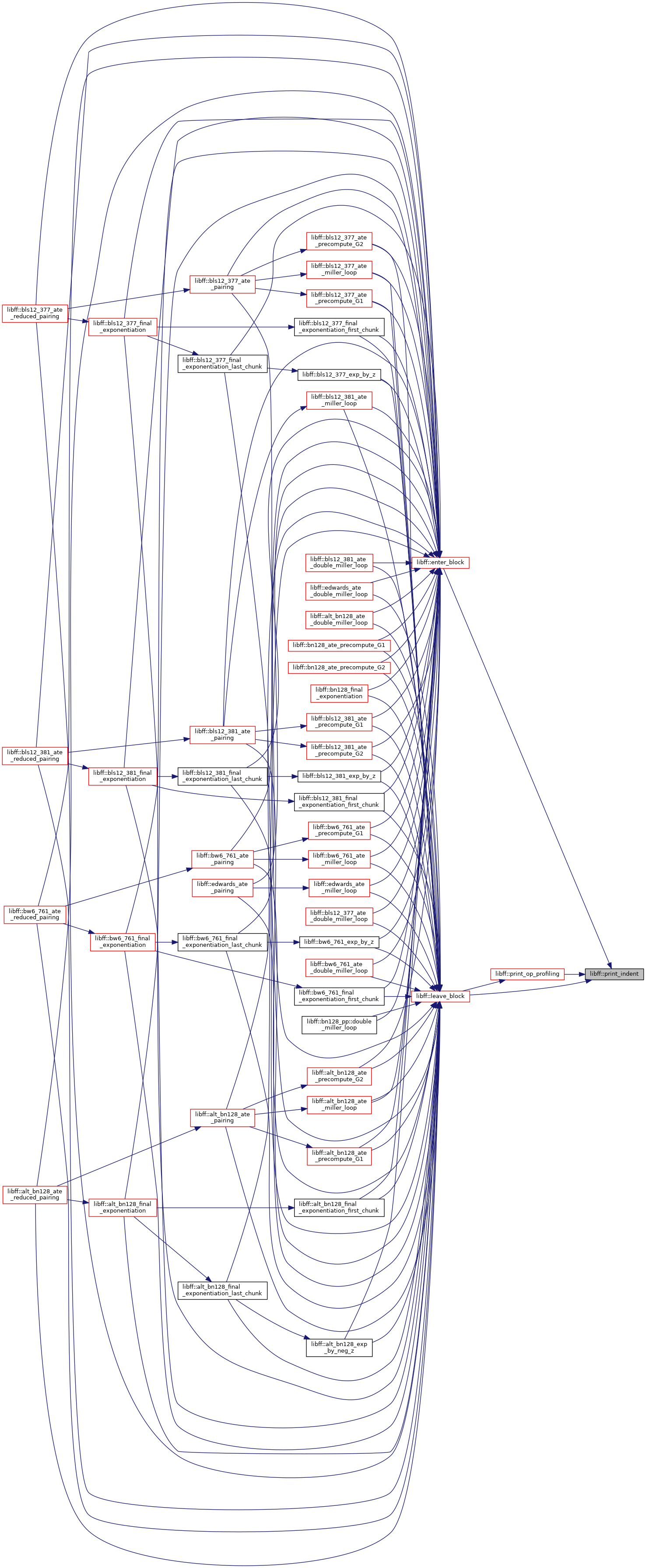
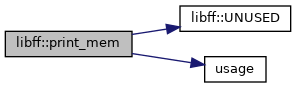
 1.8.17
1.8.17